[CF787D] legacy
题目
Rick和他的同事们研究出了一种新的有关放射的公式,于是许多坏人就在追赶他们。所以Rick希望在被坏人抓住之前把遗产给Morty。
在他们的宇宙里总共有n颗行星,每颗行星有它自己的编号(编号为1到n)。Rick所在的行星的编号是s(地球),但是他不知道Morty在哪?总所周知,Rick有一门能打开奇妙入口的枪。在这把枪的帮助下,他能打开一扇单向门去往任意一个星球(包括那把枪自己所在的星球),但是这玩意是有限制的,因为Rick用的是这玩意的免费试用版。
一般而言,他不能用这把枪打开任意一扇单向的门。但是有q个套餐在它的官网上售卖。每一次你购买了这个套餐,你就能也仅仅能使用它一次,但是你可以重复购买(如果你觉得需要多次使用的话)。
网站上的套餐有以下三种类型:
1.打开一扇从v到u的门
2.打开一扇从v到[l,r]之间任何一个的门
3.打开一扇从[l,r]到v之间任何一个的门
Rick不知道Morty在哪?但是Unity准备告诉他。于是Rick就要准备好一切。
因为Rick的预算不多,所以他想知道从他的星球出发,到达每一个星球的最少花费是多少,如果到达不了,就输出-1.
$1<=n,q<=10^5,1<=s<=n$
题解
首先,最简单的想法就是逐条添加边,但这样的时间复杂度为$O(nm)$
注意到2,3操作的点都是连续的
所以可以考虑把这些点压成一坨一坨的
如果把它缩在线段树的节点里,那么对于一堆连续的点,最多会压成$O(logn)$个点(感性理解)
也就是说,对于2,3操作,最多只会添加$O(logn)$条边。
例如,对于操作 [2,4] - > 1,构造的图如下
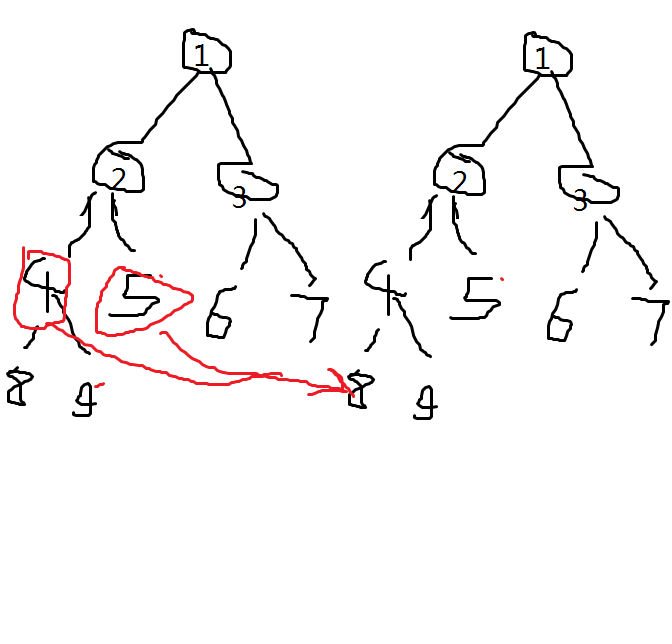
注意图中的编号是线段树节点编号。
如图,我们种两颗线段树,一棵压起点,一棵压终点
但这样我们只能走一次边,所以在原图上在稍作改造
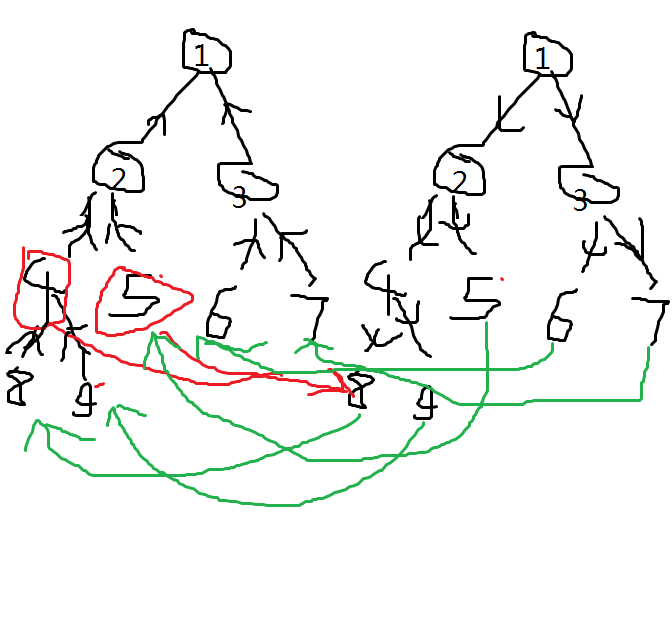
如图,我们添加了两种边
- 黑边:起点线段树子向父连接,终点线段树父向子连接
- 绿边:对应的叶子节点从终点线段树向起点线段树连接
这样,我们就可以直接在这张图上跑最短路了,
起点为s在起点线段树中的点,
记得每个点的dis要在终点树上获取
#include <iostream> #include <cstring> #include <cstdio> #include <vector> #include <queue> #include <map> using namespace std; #define N 400000 #define M 1000000 #define int long long #define mid ((l+r)>>1) #define lc id*2,l,mid #define rc id*2+1,mid+1,r #define root 1,1,n #define pr pair<int,int> vector<pr> vec[M]; int n,cnt; //获取[l,r]的点在线段树中压出来的点 void find(int id,int l,int r,int tl,int tr,vector<int> &area) { if(l>=tl&&r<=tr) { area.push_back(id); return; } if(tl<=mid) find(lc,tl,tr,area); if(tr>mid) find(rc,tl,tr,area); } //获取单点在线段树中的编号 int find2(int num) { vector<int> v; find(root,num,num,v); return v[0]; } //连接[l1,r1]->[l2,r2],即构造红边 void connect(int l1,int r1,int l2,int r2,int w) { vector<int> a,b; find(root,l1,r1,a); find(root,l2,r2,b); cnt++;//新建一个中介节点,当然在这题没有必要 for(int i=0;i<a.size();i++) vec[a[i]].push_back(make_pair(cnt,w)); for(int i=0;i<b.size();i++) vec[cnt].push_back(make_pair(b[i]+N,0)); } void build(int id,int l,int r,int num)//构造黑边 { if(l==r) return; if(!num) { vec[id*2].push_back(make_pair(id,0)); vec[id*2+1].push_back(make_pair(id,0)); } else { vec[id+N].push_back(make_pair(id*2+N,0)); vec[id+N].push_back(make_pair(id*2+1+N,0)); } build(lc,num); build(rc,num); } int s,dis[M],inq[M]; queue<int> q; void spfa() { memset(dis,0x6f,sizeof(dis)); s=find2(s); dis[s+N]=dis[s]=0; q.push(s); while(!q.empty()) { int now=q.front(); q.pop(); inq[now]=false; for(int i=0;i<vec[now].size();i++) { pr p=vec[now][i]; int t=dis[now]+p.second; if(t<dis[p.first]) { dis[p.first]=t; if(!inq[p.first]) q.push(p.first); inq[p.first]=true; } } } } signed main() { //freopen("data.txt","r",stdin); int q; cin>>n>>q>>s; cnt=2*N; build(root,0); build(root,N); for(int i=1;i<=n;i++)//构造绿边 { vector<int> v; find(root,i,i,v); int t=v[0]; vec[t+N].push_back(make_pair(t,0)); } for(int i=1;i<=q;i++) { int type,v,w,l,r,u; scanf("%lld%lld",&type,&u); if(type==1) { scanf("%lld%lld",&v,&w); connect(u,u,v,v,w); } else { scanf("%lld%lld%lld",&l,&r,&w); if(type==3) connect(l,r,u,u,w); else connect(u,u,l,r,w); } } spfa(); for(int i=1;i<=n;i++) { int t=find2(i); if(dis[t+N]<0x7fffffffffffff) printf("%lld ", dis[t+N]); else printf("-1 "); } }


