计算几何学常用公式和技巧

向量

向量的叉积

x₁*y₂-x₂*y₁

返回向量A(x1,y1)与B（x2,y2）的叉积。

同时也是以这两个向量为临边围成的平行四边形的有向面积。

当B在A前进方向的左边时值为正，

共线时为0，

右边为负。

 

由三维叉乘

扩展至

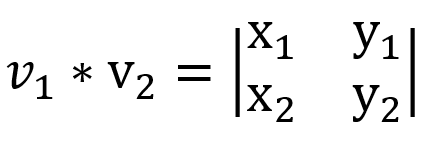
要注意的是三维叉乘得到的向量，二维叉乘得到的是数值

向量的点积

x₁*x₂₊y₁*y₂

向量的垂线

 (x,y)与（y,-x）垂直，垂足为两向量的起点。

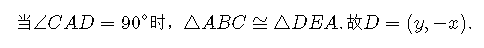
旋转向量

设向量(x,y)逆时针旋转r(弧度)后得到(x₁,y₁),则

x₁=x*cos(r)-y*sin(r)

y₁=x*sin(r)+y*cos(r)

推导请看

这里

求点的极角（C/C++）

atan2(y,x)

返回该点与原点的连线与正x轴的夹角，从-π到π（弧度）。

可以将其乘上180/π，得到角度。

注意是先y后x。

 直线

两点确定直线

若一直线上ax+by+c=0有(x1,y1),(x2,y2)两点，则：

a = y₂ - y₁;
b = x₁ -x₂;
c =x₂*y₁ - x₁*y₂;

可以自己列两个解来模拟

两直线交点

若两直线方程为:

则交点为：

通过解方程推导。

比较直线斜率

 用乘法比较，除法会掉精度

去除共线的点的贡献

枚举两个点，计算其斜率，然后枚举其他点，比较其他点与第一个点的斜率是否相同。

$O(n^3)$