图
1.学习总结
1.1图的思维导图
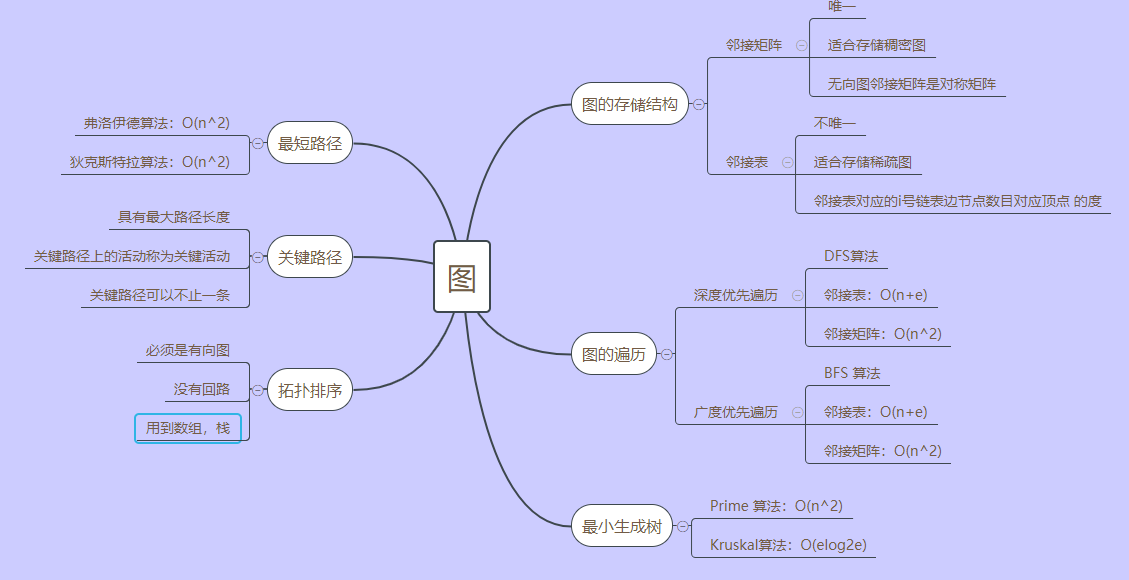
1.2 图结构学习体会
1.深度遍历算法和广度遍历算法:深度优先从初始定点开始访问其邻接顶点,然后再访问该顶点的未被访问过的邻接顶点;广度优先是从初始顶点开始访问,接着访问初始顶点的所有未被访问过的邻接点,然后按照邻接点的次序依次访问每一个顶点的未被访问过的点,直到所有顶点被访问;理解起来相对容易,做题时也大部分能懂。
2.Prim和Kruscal算法:prim算法把顶点分成已选和未选,但相比来说kruscal算法找最小边更为精确,代码量也小。
3.Dijkstra算法:时间复杂度为O(n²)。是从一个顶点到其余各顶点的最短路径算法,解决的是有向图中最短路径问题。该算法主要特点是以起始点为中心向外层层扩展,直到扩展到终点为止。
4.拓扑排序算法:为广度优先搜索,必须要为有向图,若出现环路则为错误。
总的来说,这章理解方面还行,课堂派的题也能做懂,对于最短路径和最小生成树概念以及算法过程都理解,但是在代码实现方面有很大的缺陷,不知道怎么转换成代码,没思路无从下手。
2.PTA实验作业
1.1 题目1: 7-1 图着色问题
1.2 设计思路
通过参考网上的算法知道了其核心在通过遍历找到所有的问题子集 ,在递归遍历的时候,都在加一个判断,将那些明显不满足条件的情况给直接排出。对一颗树的遍历每个节点相当走到此时的状态,然后再判断此时的状态是否能继续走下去,如果不能就将其回溯到上一个节点,避免浪费时间。


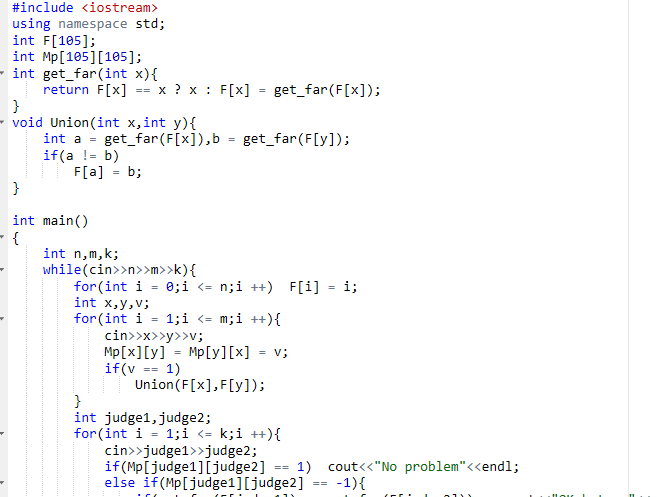


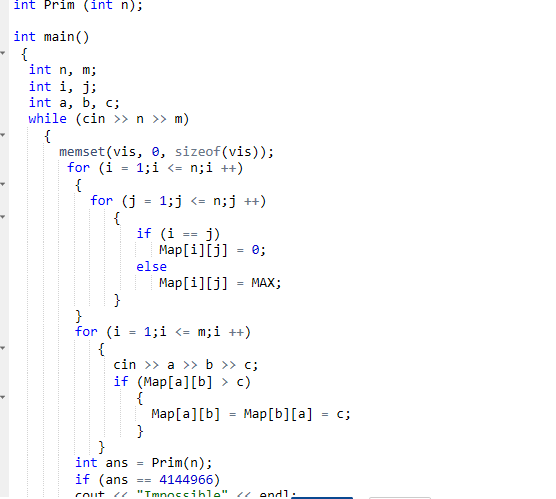


没有解决不连通情况,增加一个深度遍历来判断,但是编译错误,后来百度发现可以直接在prime函数里进行判断,改完后就可以了。

旅游规划 (25分)
有了一张自驾旅游路线图,你会知道城市间的高速公路长度、以及该公路要收取的过路费。现在需要你写一个程序,帮助前来咨询的游客找一条出发地和目的地之间的最短路径。如果有若干条路径都是最短的,那么需要输出最便宜的一条路径。
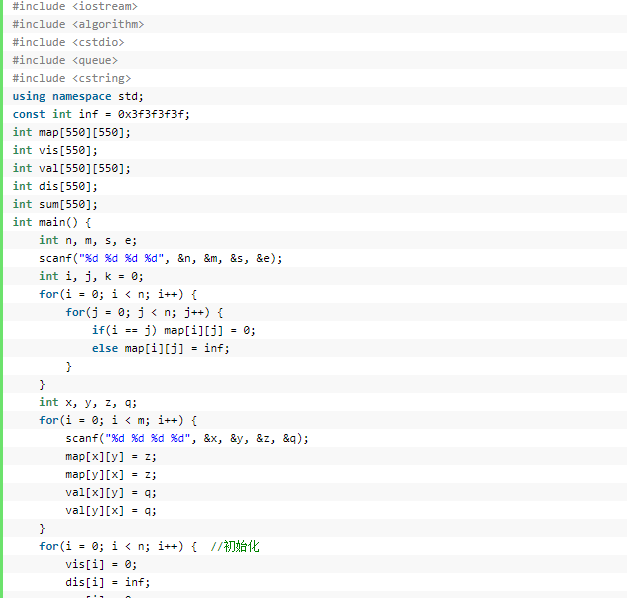
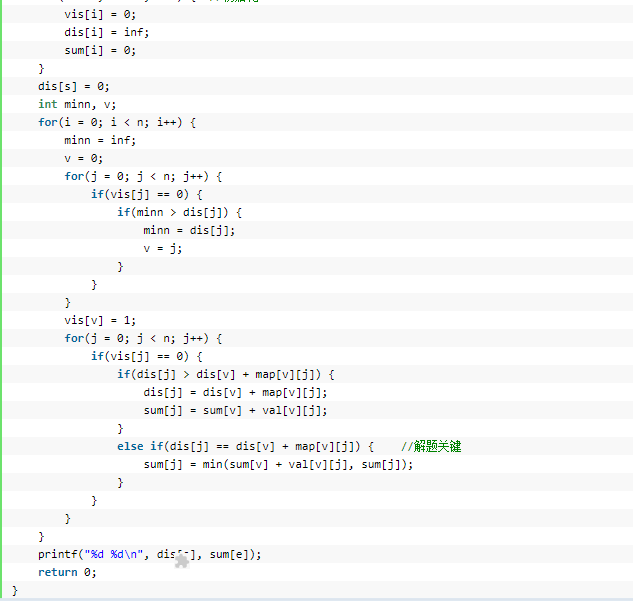
设计思路:定义数组ways[505][505][2] 用于储存路径的长度;
费用 dist[505],cost[505];分别储存由st出发点到个点的最短路径及其费用
visited[505] = {0} 储存个点是否加入集合中
初始化数组ways,dist,cost
for i=0 to M 循环找到最短路径或最少金额
for j=0 to M 找到与初始顶点最近的顶点,用mindis保存该顶点
visited标记该顶点已被访问过
for j=0 to M
如果顶点未被访问过,且到起始顶点的路径大于最短路径
则将最短路径附给dist[j];同时金额也相应改变
如果距离相等则只改变金额
end


