ACM数论之旅10---大组合数-卢卡斯定理（在下卢卡斯，你是我的Master吗？(。-`ω´-) ）
记得前几章的组合数吧
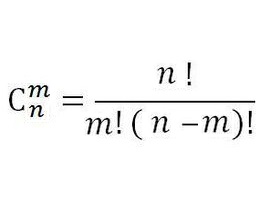
我们学了O(n^2)的做法，加上逆元，我们又会了O(n)的做法
现在来了新问题，如果n和m很大呢，
比如求C(n, m) % p ， n<=1e18,m<=1e18,p<=1e5
看到没有，n和m这么大，但是p却很小，我们要利用这个p
（数论就是这么无聊的东西，我要是让n=1e100，m=1e100，p=1e100你有本事给我算啊(°□°)，还不是一样算不出来）
然后，我们著名的卢卡斯（Lucas）在人群中站了出来(｀･д･´)说：“让老子来教你这题”
卢卡斯说：
C(n, m) % p = C(n / p, m / p) * C(n%p, m%p) % p
对于C(n / p, m / p)，如果n / p 还是很大，可以递归下去，一直到世界的尽头
众人闻此言，无不惊叹，妙哉！妙哉！
（笑死我了o(*≧▽≦)ツ┏━┓拍桌狂笑）
（不要问我证明过程，我不费(´･ω･｀)）
然后上代码
1 LL Lucas(LL n, LL m, int p){ 2 return m ? Lucas(n/p, m/p, p) * comb(n%p, m%p, p) % p : 1; 3 }
简洁易懂<(￣︶￣)>
实战一下吧
hdu 5446
http://acm.hdu.edu.cn/showproblem.php?pid=5446
题意：
给你三个数n, m, k
第二行是k个数，p1,p2,p3...pk
所有p的值不相同且p都是质数
求C(n, m) % (p1*p2*p3*...*pk)的值
范围：1≤m≤n≤1e18，1≤k≤10，pi≤1e5，保证p1*p2*p3*...*pk≤1e18
AC代码：
1 #include<cstdio> 2 typedef long long LL; 3 const int N = 100000 + 5; 4 LL mul(LL a, LL b, LL p){//快速乘，计算a*b%p 5 LL ret = 0; 6 while(b){ 7 if(b & 1) ret = (ret + a) % p; 8 a = (a + a) % p; 9 b >>= 1; 10 } 11 return ret; 12 } 13 LL fact(int n, LL p){//n的阶乘求余p 14 LL ret = 1; 15 for (int i = 1; i <= n ; i ++) ret = ret * i % p ; 16 return ret ; 17 } 18 void ex_gcd(LL a, LL b, LL &x, LL &y, LL &d){ 19 if (!b) {d = a, x = 1, y = 0;} 20 else{ 21 ex_gcd(b, a % b, y, x, d); 22 y -= x * (a / b); 23 } 24 } 25 LL inv(LL t, LL p){//如果不存在，返回-1 26 LL d, x, y; 27 ex_gcd(t, p, x, y, d); 28 return d == 1 ? (x % p + p) % p : -1; 29 } 30 LL comb(int n, int m, LL p){//C(n, m) % p 31 if (m < 0 || m > n) return 0; 32 return fact(n, p) * inv(fact(m, p), p) % p * inv(fact(n-m, p), p) % p; 33 } 34 LL Lucas(LL n, LL m, int p){ 35 return m ? Lucas(n/p, m/p, p) * comb(n%p, m%p, p) % p : 1; 36 } 37 LL china(int n, LL *a, LL *m){//中国剩余定理 38 LL M = 1, ret = 0; 39 for(int i = 0; i < n; i ++) M *= m[i]; 40 for(int i = 0; i < n; i ++){ 41 LL w = M / m[i]; 42 //ret = (ret + w * inv(w, m[i]) * a[i]) % M;//这句写了会WA，用下面那句 43 ret = (ret + mul(w * inv(w, m[i]), a[i], M)) % M; 44 //因为这里直接乘会爆long long ,所以我用快速乘(unsigned long long也是爆掉，除非用高精度) 45 } 46 return (ret + M) % M; 47 } 48 int main(){ 49 int T, k; 50 LL n, m, p[15], r[15]; 51 scanf("%d", &T); 52 while(T--){ 53 scanf("%I64d%I64d%d", &n, &m, &k); 54 for(int i = 0; i < k; i ++){ 55 scanf("%I64d", &p[i]); 56 r[i] = Lucas(n, m, p[i]); 57 } 58 printf("%I64d\n", china(k, r, p)); 59 } 60 }
我们知道题目要求C(n, m) % (p1*p2*p3*...*pk)的值
其实这个就是中国剩余定理最后算出结果后的最后一步求余
那C(n, m)相当于以前我们需要用中国剩余定理求的值
然而C(n, m)太大，我们只好先算出
C(n, m) % p1 = r1
C(n, m) % p2 = r2
C(n, m) % p3 = r3
.
.
.
C(n, m) % pk = rk
用Lucas，这些r1,r2,r3...rk可以算出来
然后又是用中国剩余定理求答案
全都是套路。。。
