博客作业06--图
一、学习总结
1.1、图的思维导图
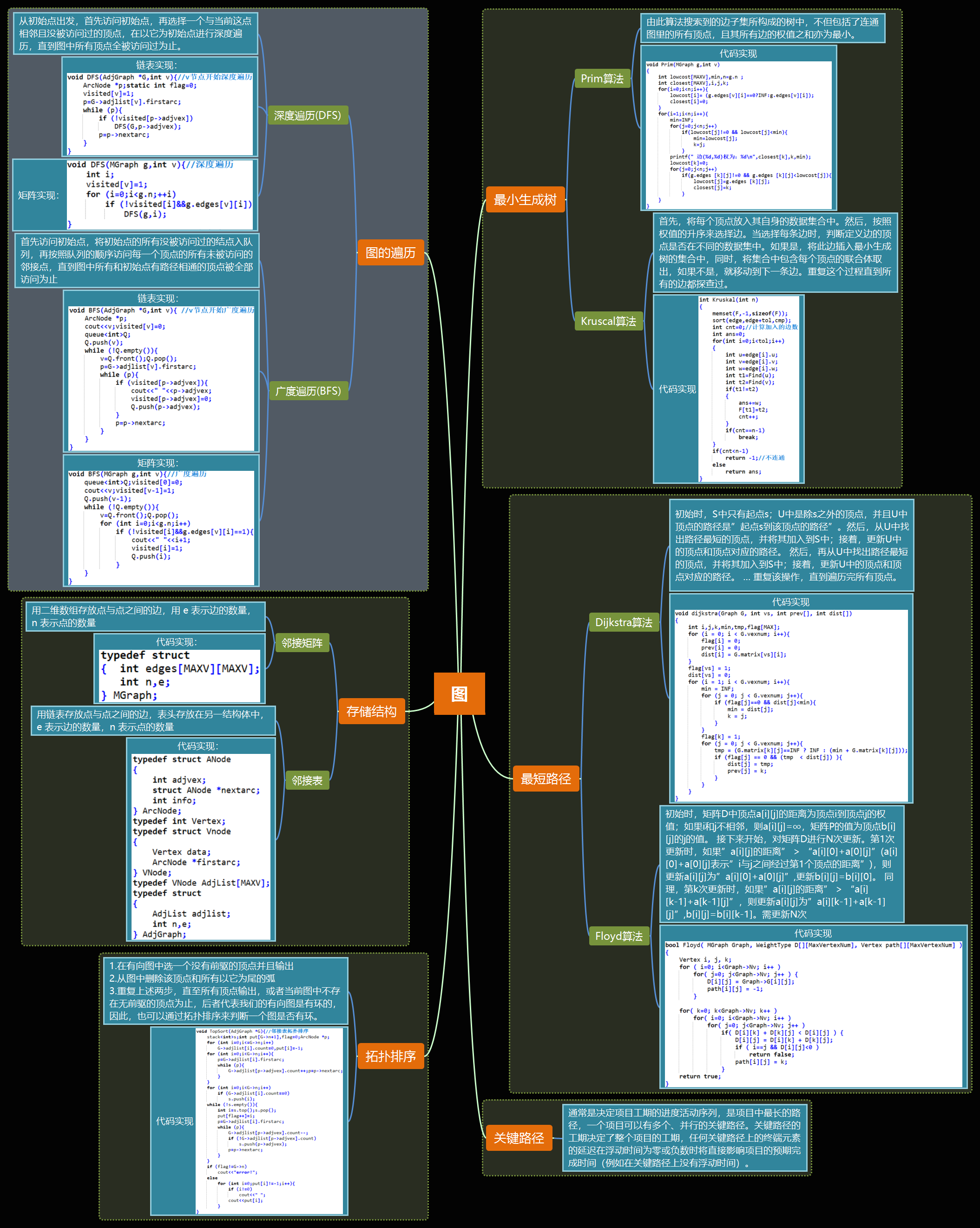
1.2、图结构学习体会
深度遍历算法
- 使用递归方式,一个结点再往下一个结点的遍历,不遍历已访问过的结点
广度遍历算法
- 用队列的方式,将一个结点的周边结点扫入队列中,再按出队的顺序依次访问,重复操作。
Prim和Kruscal算法
- 都是生成最小生成树的算法。
- Prim 算法从任意一个顶点开始,每次选择一个与当前顶点集最近的一个顶点,并将两顶点之间的边加入到树中。Prim 算法在找当前最近顶点时使用到了贪婪算法。
- Kruscal 算法原理:首先,将每个顶点放入其自身的数据集合中。然后,按照权值的升序来选择边。当选择每条边时,判断定义边的顶点是否在不同的数据集中。如果是,将此边插入最小生成树的集合中,同时,将集合中包含每个顶点的联合体取出,如果不是,就移动到下一条边。重复这个过程直到所有的边都探查过。
Dijkstra算法
- 特征:使用了广度优先搜索解决赋权有向图或者无向图的单源最短路径问题,算法最终得到一个最短路径树。
- 原理:按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度
拓扑排序算法
- 通常是决定项目工期的进度活动序列,是项目中最长的路径,一个项目可以有多个、并行的关键路径。关键路径的工期决定了整个项目的工期,任何关键路径上的终端元素的延迟在浮动时间为零或负数时将直接影响项目的预期完成时间(例如在关键路径上没有浮动时间)。
二、PTA实验作业
2.1.1、7-1 图着色问题
2.1.2、设计思路
用二维数组 es[e][2] 存放输入的边集// e 是输入的行数
while (颜色分配方案 m-- 不为0)
color 数组存放每个结点对应的颜色,flag 等于 1 作为标志
用 map<int,int> col 统计输入颜色的个数
输入 color 数组的内容,并把对应的 col 内容置为1
if ( col 的元素个数不等于 k ) 输出 “No” ;
else
for(遍历边集 es )
if ( es 的同一行的两个元素对应的颜色相同 )
输出 “No”,flag 等于 0
if ( flag 为真 )
输出 “Yes”
end for
end while
2.1.3、代码截图


2.1.4、PTA提交列表说明
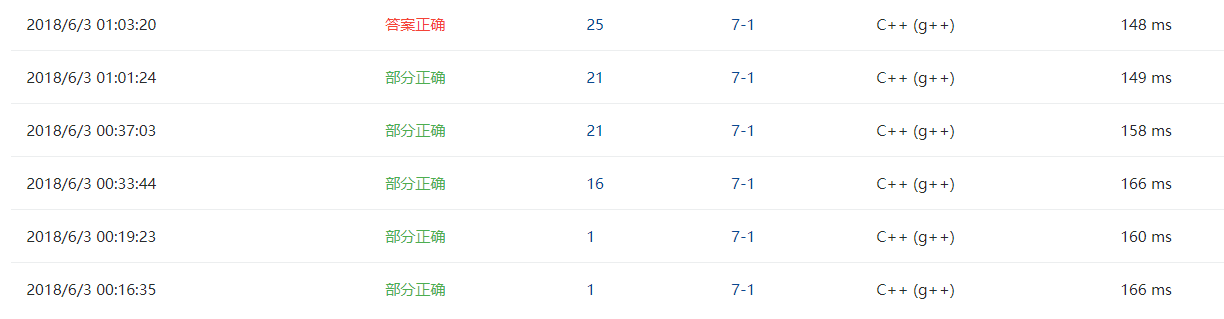
- 之前没想到可以用边集来判断,用了邻接表、邻接矩阵存放边,用 DFS、BFS 来判断,于是很多错的。
- 后来发现只需要对颜色的个数特别判断,另外的可以循环判断边集的结点颜色是否相等,就通过了。
2.2.1、7-4 公路村村通
2.2.2、设计思路
MAX 定义为 1050
邻接矩阵 edge [MAX][MAX] ,Vnum 统计遍历过的结点数,sum 存放路径和
将 low 数组初始化为邻接矩阵中起始点的那一行
for i = 0 to n-1
min = MAX,k;
遍历 low 数组,找到数组中最小且不为 0 的边,将 min 定位到这个边的权重,k 定位到这个边在数组中的位置
if( min == MAX ) 说明没有边,结束循环
sum 加上最小边,low 数组中 k 位置设为 0 ,Vnum 记录遍历的结点数
for j = 1 to n
if( low[j] 存在且 edge[k][j] 小于 low[j] )把 low[j] 的值更新为 edge[k][j] 的值
end for j
end for i
if ( Vnum 不等于 n )输出 -1
else 输出 sum 的值
2.2.3、代码截图


2.2.4、PTA提交列表说明
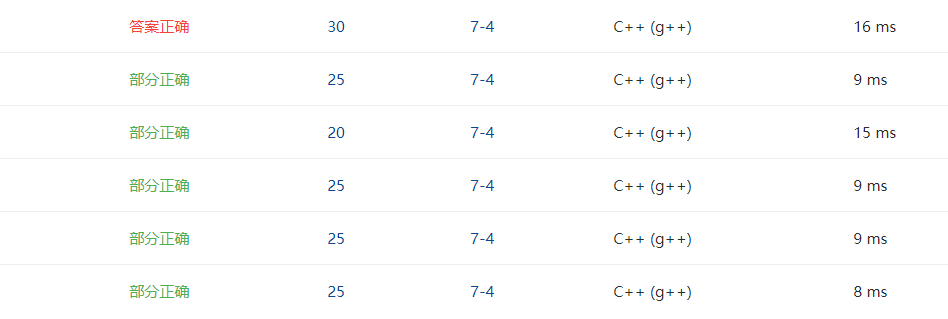
- 应该使用普里姆算法,但是一开始写的时候没想到。
- 没有在普里姆算法里加上
if (min==MAX)一句,然后就错了。
2.3.1、7-7 旅游规划
2.3.2、设计思路
MAX 取值为 550
邻接矩阵 edge[MAX][MAX] 存放 距离 权重;邻接矩阵 costs[MAX][MAX] 存放 路费 权重,最短路径数组 dist[MAX],最小花费数组 cost[MAX],记录遍历结点的数组 visited[MAX] = { 0 }
将 dist 数组初始化为初始点的 edge 的那一行,cost 数组初始化为初始点的 costs 的那一行
将初始点的 dist 归零,对应的 visited 数组位置置为 1
for i = 0 to n-2
min = MAX,k;
遍历 dist 数组,找到数组中最小且对应结点未被遍历的边,将 min 定位到这个边的权重,k 定位到这个边在数组中的位置
将 k 结点的 visited 置为 1
for j = 0 to n-1
if( j 结点未被遍历且初始点到 k 结点的距离加上 k 结点到 j 结点的距离比初始点到 j 结点的距离小) 更新 dist[j] 为 dist[k]+edge[k][j]
else if( j 结点未被遍历且 dist[j] == dist[k]+edge[k][j] 且 costs[k][j]+cost[k] 小于 cost[j] ) 更新 cost[j] 为 costs[k][j]+cost[k]
end for j
end for i
2.3.3、代码截图


2.3.4、PTA提交列表说明
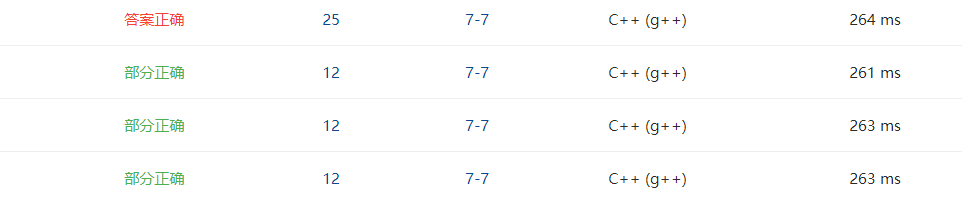
- 这里的三次错误是因为输出的地方,要输出的是 dist[d] 和 cost[d],我把 d 输出了。
三、截图本周题目集的PTA最后排名
3.1、PTA排名

3.2、我的得分:2.5
四、阅读代码
- SPFA算法
地址:https://blog.csdn.net/qq_35644234/article/details/61614581
bool Graph::SPFA(int begin) {
bool *visit;
//visit用于记录是否在队列中
visit = new bool[this->vexnum];
int *input_queue_time;
//input_queue_time用于记录某个顶点入队列的次数
//如果某个入队列的次数大于顶点数vexnum,那么说明这个图有环,
//没有最短路径,可以退出了
input_queue_time = new int[this->vexnum];
queue<int> s; //队列,用于记录最短路径被改变的点
/*
各种变量的初始化
*/
int i;
for (i = 0; i < this->vexnum; i++) {
visit[i] = false;
input_queue_time[i] = 0;
//路径开始都初始化为直接路径,长度都设置为无穷大
dis[i].path = this->node[begin-1].data + "-->" + this->node[i].data;
dis[i].weight = INT_MAX;
}
//首先是起点入队列,我们记住那个起点代表的是顶点编号,从1开始的
s.push(begin - 1);
visit[begin - 1] = true;
++input_queue_time[begin-1];
//
dis[begin - 1].path =this->node[begin - 1].data;
dis[begin - 1].weight = 0;
int temp;
int res;
ArcNode *temp_node;
//进入队列的循环
while (!s.empty()) {
//取出队首的元素,并且把队首元素出队列
temp = s.front(); s.pop();
//必须要保证第一个结点不为空
if (node[temp].firstarc)
{
temp_node = node[temp].firstarc;
while (temp_node) {
//如果边<temp,temp_node>的权重加上temp这个点的最短路径
//小于之前temp_node的最短路径的长度,则更新
//temp_node的最短路径的信息
if (dis[temp_node->adjvex].weight > (temp_node->weight + dis[temp].weight)) {
//更新dis数组的信息
dis[temp_node->adjvex].weight = temp_node->weight + dis[temp].weight;
dis[temp_node->adjvex].path = dis[temp].path + "-->" + node[temp_node->adjvex].data;
//如果还没在队列中,加入队列,修改对应的信息
if (!visit[temp_node->adjvex]) {
visit[temp_node->adjvex] = true;
++input_queue_time[temp_node->adjvex];
s.push(temp_node->adjvex);
if (input_queue_time[temp_node->adjvex] > this->vexnum) {
cout << "图中有环" << endl;
return false;
}
}
}
temp_node = temp_node->next;
}
}
}
//打印最短路径
return true;
}
SPFA(队列优化)算法是求单源最短路径的一种算法,它还有一个重要的功能是判断负环,在Bellman-ford算法的基础上加上一个队列优化,减少了冗余的松弛操作,是一种高效的最短路算法。但是时间效率是不稳定的,即它对于不同的图所需要的时间有很大的差别。
在最好情形下,每一个节点都只入队一次,则算法实际上变为广度优先遍历,其时间复杂度仅为O(E)。另一方面,存在这样的例子,使得每一个节点都被入队(V-1)次,此时算法退化为Bellman-ford算法,其时间复杂度为O(VE)。
SPFA算法在负边权图上可以完全取代Bellman-ford算法,另外在稀疏图中也表现良好。但是在非负边权图中,为了避免最坏情况的出现,通常使用效率更加稳定的Dijkstra算法,以及它的使用堆优化的版本。通常的SPFA算法在一类网格图中的表现不尽如人意。



