博客作业04--树

一、学习总结

1.1、树结构思维导图

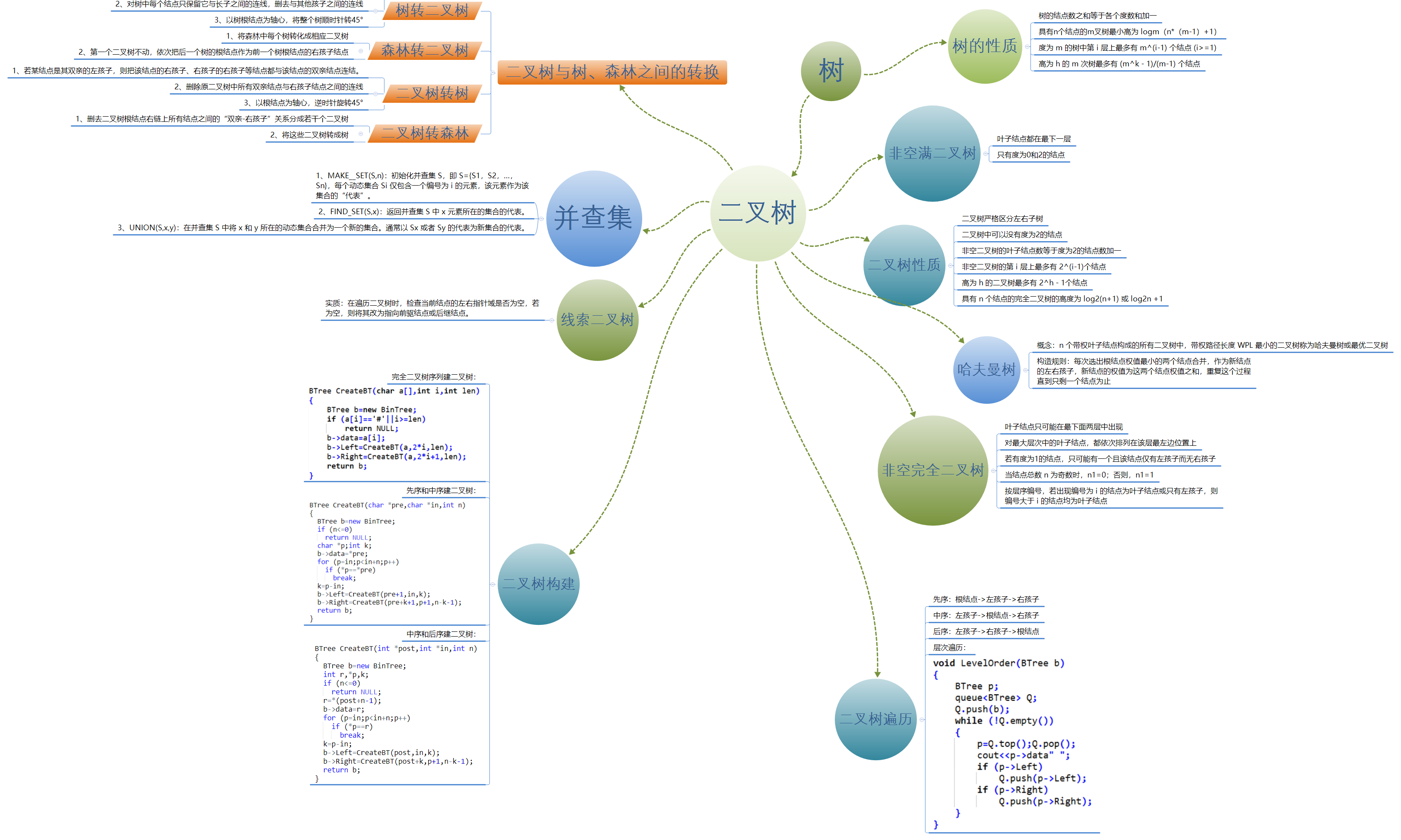
1.2、树结构学习体会

  • 树的操作大多通过递归算法实现，而递归算法是我目前还比较难以熟练运用的。
  • 并查集，书中写的理解起来比较难。
  • 在哈夫曼树里，WPL 的值也等于所有非叶子结点值之和，我对于哈夫曼树的构建还不是很熟悉。
  • 线索二叉树还在原来二叉树的根结点上增加了一个root结点。
  • 树的知识点有点散乱，一些性质（如满二叉树等）还是要熟练掌握的。

二、PTA实验作业

2.1.1、6-4 jmu-ds-表达式树

2.1.2、设计思路

void trans(string exp,char post[])
作用：将输入的中缀表达式转换成后缀表达式。（直接把之前写过的题目的代码拿来修改使用，略过）。

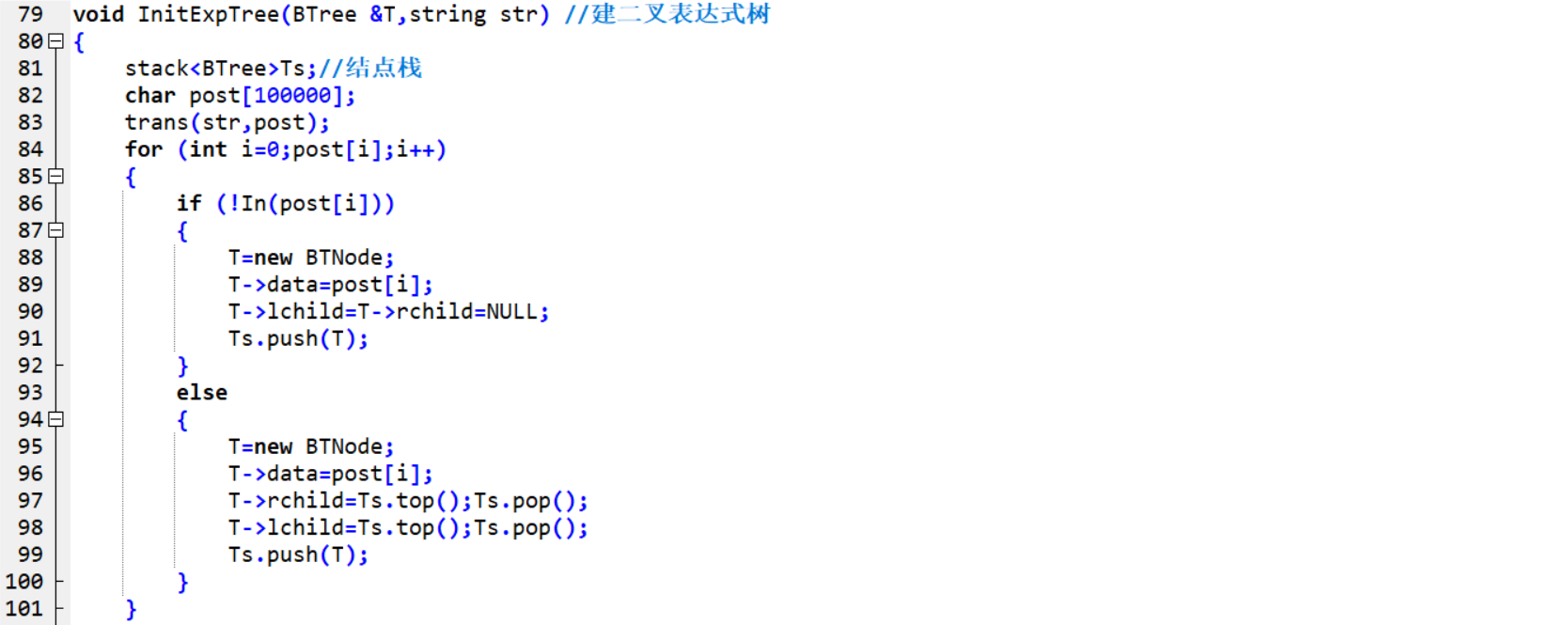
void InitExpTree(BTree &T,string str)    //建立二叉表达式树
    首先将输入的中缀表达式 str 转换成后缀表达式 post ；建立一个结点栈。
    遍历循环 post 数组：
        如当前元素为数字，将其结点化，左右孩子置为空，存入结点栈；
        如为符号，将其结点化，将栈中的第一、第二个结点弹出，成为符号结点的右、左孩子，再存入栈中。
    最后取栈顶结点给 T

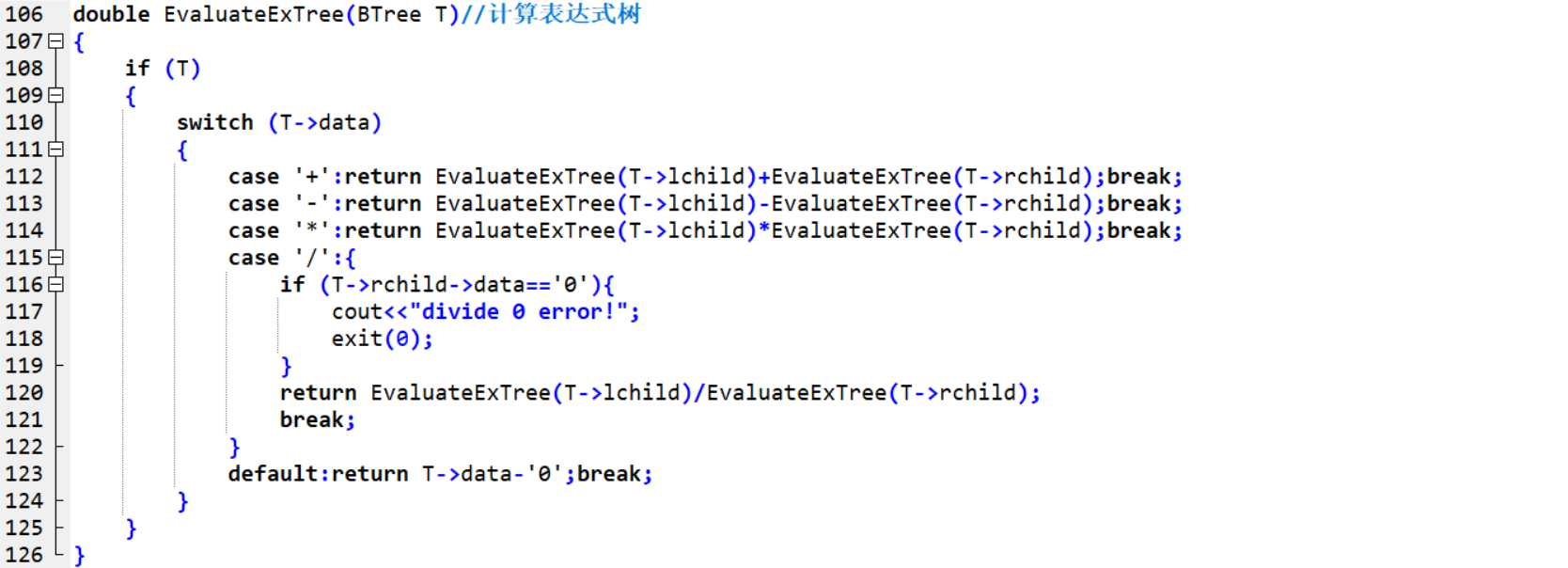
double EvaluateExTree(BTree T)    //计算表达式树
    当结点 T 不为空的时候，若结点 T 存放的是符号，则返回其左孩子与右孩子的符号运算结果（特殊情况：若符号为 / ，需判断其右孩子是否为 0 ）；若是数字，则返回数字。

2.1.3、代码截图






2.1.4、PTA提交列表说明

  • 段错误：一开始是想建立两个栈，边读取数组元素边处理，结果在DEVC上可以运行（得到正确答案），PTA上出现段错误。然后调试后发现会出现结点栈已空但是还要读取结点栈栈顶元素的情况。于是改成。

2.2.1、7-8 jmu-ds-二叉树叶子结点带权路径长度和

2.2.2、设计思路

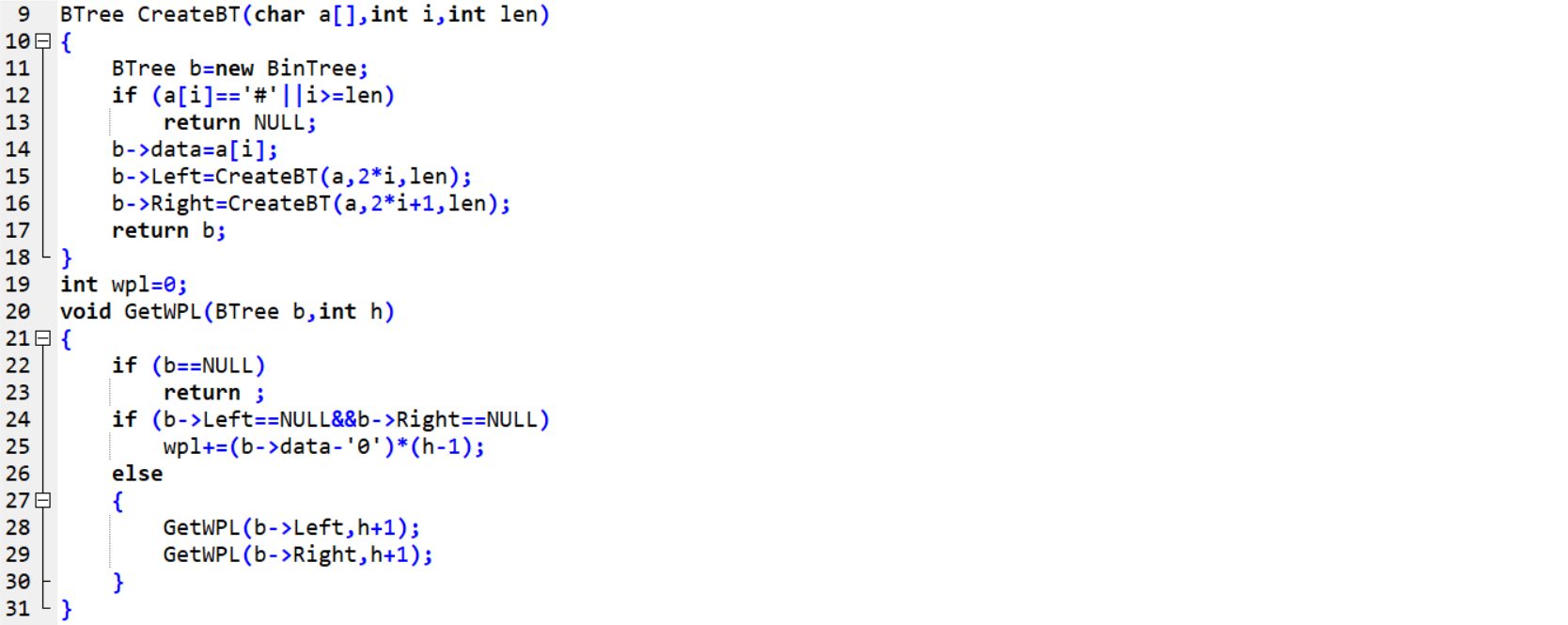
BTree CreateBT(char a[],int i,int len)    //完全二叉树层次顺序建立二叉树
    如果当前数组元素为空或 i 大于等于 len （数组长度），返回空；
    否则将当前数组元素存入新建结点，递归构建左、右孩子。
    最后返回结点。

void GetWPL(BTree b,int h)    //计算叶子结点带权路径长度，用全局变量 wpl 存放和
    当结点存在时，若该结点为叶子结点，将其结点乘以高度存进 wpl ，递归左、右孩子。

2.2.3、代码截图



2.2.4、PTA提交列表说明

  • 答案错误：构建二叉树的函数中，我一开始写成当 i 大于 len 时，忽略了 i 等于 len 的情况。

2.3.1、7-7 修理牧场

2.3.2、设计思路

    priority_queue<int,vector<int>,greater<int> >Q;//优先队列存放元素
    在队列中元素不为一时，循环将两个元素出队列，将他们的和放入 wpl ，再把这个和入队列。
    最后输出 wpl

2.3.3、代码截图

2.3.4、PTA提交列表说明

  • 运行超时：原先没有使用优先队列，用数组模拟这个过程，由于每次加入两个元素的和都要进行一次时间复杂度为O（nlogn）的排序，所以这个模拟过程时间复杂度为O（n²logn），超出题目要求。

三、截图本周题目集的PTA最后排名

3.1、PTA排名

3.2、我的得分：2.5

四、阅读代码

7-5 家谱处理（网上收集）

#include <stdio.h>  
#include <string.h>  
struct people {  
    int num;  
    char name[15];  
    char father[15];  
}t1[101];  
int main()  
{  
    int n, m,i; char na[71];  
    scanf("%d %d", &n, &m);  
    getchar();  
    for (i=0;i<n;i++) {    
        t1[i].num = 0;  
        gets(na);  
        int l = strlen(na),j;  
        for (j = 0; j < l; j++) {  
            if (na[j] == ' ') t1[i].num++;  
            else {  
                strcpy(t1[i].name, na + j);  
                break;  
            }  
        }  
        if (!t1[i].num) strcpy(t1[i].father, "root");  
        else {  
            int k;  
            for (k = i-1; k >= 0; k--) {  
                if (t1[i].num>t1[k].num) {  
                    strcpy(t1[i].father, t1[k].name);  
                    break;  
                }  
            }  
        }  
    }//out  
    char a[15], b[10], c[15], d[10];  
    for (i = 0; i < m; i++) {  
        int k;  
        scanf("%s %s %s %s %s %s", &a, &d, &d, &b, &d, &c);  
        if (b[0] == 'c') {  
            for (k = 0; k < n; k++) {  
                if (!strcmp(t1[k].name, a)) {  
                    if (!strcmp(t1[k].father, c))  
                        printf("True\n");  
                    else printf("False\n");  
                    break;  
                }  
            }  
        }  
        else if (b[0] == 'p') {  
            for (k = 0; k < n; k++) {  
                if (!strcmp(t1[k].name, c)) {  
                    if (!strcmp(t1[k].father, a))  
                        printf("True\n");  
                    else printf("False\n");  
                    break;  
                }  
            }  
        }  
        else if (b[0] == 's') {  
            char num1[15], num2[15];  
            for (k = 0; k < n; k++) {  
                if (!strcmp(t1[k].name, a)) strcpy(num1, t1[k].father);  
                if (!strcmp(t1[k].name, c)) strcpy(num2, t1[k].father);  
            }  
            if(!strcmp(num1,num2)) printf("True\n");  
            else printf("False\n");  
        }  
        else if (b[0] == 'a') {  
            char num1[15];  
            for (k = 0; k < n; k++)   
                if (!strcmp(t1[k].name, c)) strcpy(num1, t1[k].father);  
            while (strcmp(num1, a) && strcmp(num1, "root")) {  
                for (k = 0; k < n; k++)  
                    if (!strcmp(t1[k].name, num1)) strcpy(num1, t1[k].father);  
            }  
            if(!strcmp(num1,"root")) printf("False\n");  
            else printf("True\n");  
        }  
        else if (b[0] == 'd') {  
            char num1[15];  
            for (k = 0; k < n; k++)  
                if (!strcmp(t1[k].name, a)) strcpy(num1, t1[k].father);  
            while (strcmp(num1, c) && strcmp(num1, "root")) {  
                for (k = 0; k < n; k++)  
                    if (!strcmp(t1[k].name, num1)) strcpy(num1, t1[k].father);  
            }  
            if (!strcmp(num1, "root")) printf("False\n");  
            else printf("True\n");  
        }  
        getchar();  
    }  
    return 0;  
}

五、代码Git提交记录截图

posted @ 2018-05-05 19:40  那就这个名字  阅读(202)  评论(0)  编辑  收藏  举报