博客作业01-抽象数据类型

#一、作业内容

• 用ADT的抽象数据模型描述你的有理数数据类型。

    ADT Rational {
        数据对象：D={e1,e2|e1,e2∈I(I为整数集)}
        数据关系：R1={e1为有理数的分子，e2为有理数的分母且大于0}
        操作集：
            IntoFraction(& T, e1, e2)
            DestoryFraction(& T)
            ModifyFraction(& T, e, i)
            ArithmeticFraction(& T1,& T2,& T3, flag)
            SimplifyFraction(& nume, & deno)
            FindMiniMultiple( e1, e2)
            ReturnFindNum(& T1,& T2,& T3, flag)
            TakeTMultiple(& T, i)
    } ADT Rational

#二、数据结构、函数说明

• 头文件：

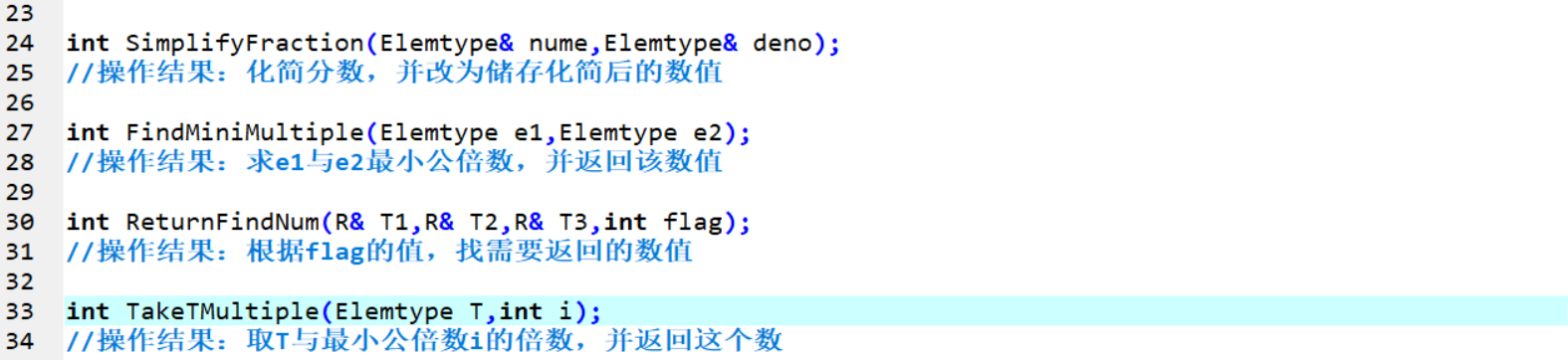
#三、代码实现说明

##IntoFraction(R& T,Elemtype e1,Elemtype e2)

##DestoryFraction(R& T)

##ModifyFraction(R& T,Elemtype e,int i)

##ArithmeticFraction(R& T1,R& T2,R& T3,int flag)

##SimplifyFraction(Elemtype& nume,Elemtype& deno)

##FindMiniMultiple(Elemtype e1,Elemtype e2)

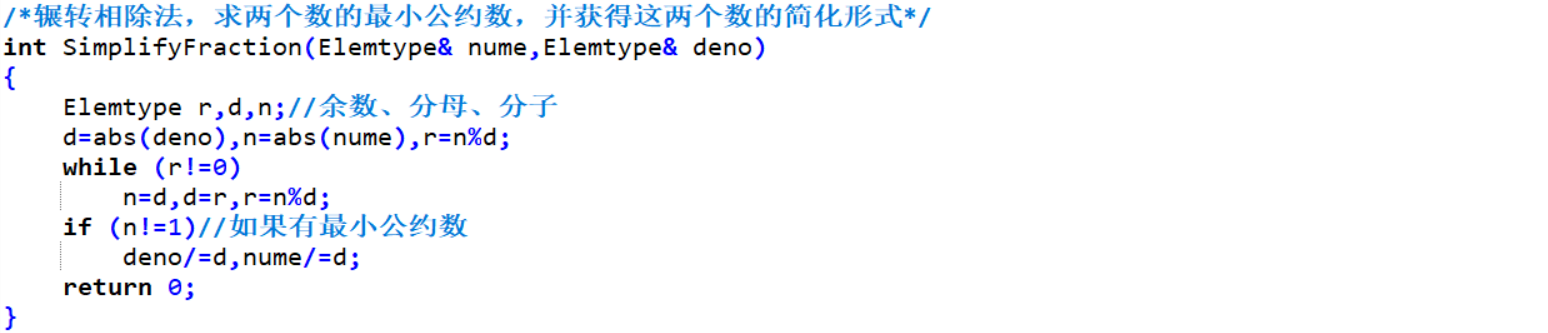
##ReturnFindNum(R& T1,R& T2,R& T3,int flag)

##TakeTMultiple(R& T,int i)

#四、代码互评

#五、结果展示

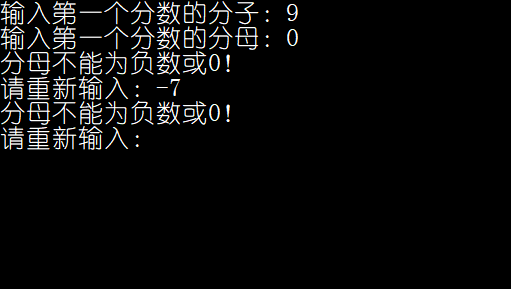
##1：分母为小于等于0的数

##2：在已经删除T1下再次删除T1

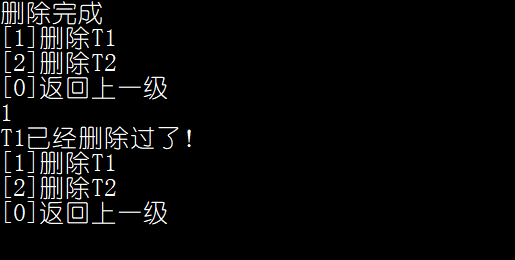
##3：在T1、T2被删除之后

##4：T1（-6/8）、T2（5/6）的四则运算

• 加法

• 减法

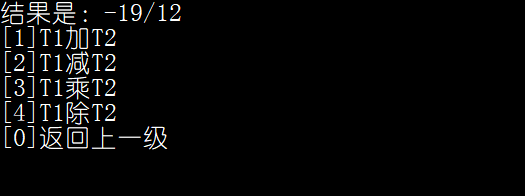
• 乘法

• 除法

##5：T1（12/36）、T2（9/128）的四则运算

• 加法

• 减法

• 乘法

• 除法

##6：T1（-9/45）、T2（-7/65）的四则运算

• 加法

• 减法

• 乘法

• 除法

##7：返回查询值（6的条件下）

• 返回T1的分子

• 返回T1的分母

• 返回T2的分子

• 返回T2的分母

##8：修改T1或T2的分子或分母（6的条件下）

• 修改T1的分子

• 修改T1的分母（修改之后是-8/72，自动化简成-1/9）

• 修改T2的分子

• 修改T2的分母（修改成的是9/108）

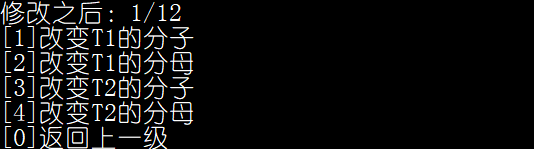
#六、总结

• 抽象数据类型是指一组定义在一个数学模型上的操作及该模型。需要通过固有的数据类型（如int之类）来实现。
• 对于现实的实际问题，可以定义对应的抽象数据类型来完成一系列定义和操作，是抽象数据类型的基本运用。