课时八、EM算法(最大期望算法)
复习Jensen不等式

引子:K-means算法

EM算法
-
在统计计算中,最大期望(EM)算法是在概率(probabilistic)模型中寻找参数最大似然估计或者最大后验估计的算法,其中概率模型依赖于无法观测的隐藏变量(Latent Variable)。
-
最大期望经常用在机器学习和计算机视觉的数据聚类(Data Clustering)领域。
-
可以有一些比较形象的比喻说法把这个算法讲清楚。
比如说食堂的大师傅炒了一份菜,要等分成两份给两个人吃,显然没有必要拿来天平一点一点的精确的去称分量,最简单的办法是先随意的把菜分到两个碗中,然后观察是否一样多,把比较多的那一份取出一点放到另一个碗中,这个过程一直迭代地执行下去,直到大家看不出两个碗所容纳的菜有什么分量上的不同为止。(来自百度百科) -
EM算法就是这样,假设我们估计知道A和B两个参数,在开始状态下二者都是未知的,并且知道了A的信息就可以得到B的信息,反过来知道了B也就得到了A。可以考虑首先赋予A某种初值,以此得到B的估计值,然后从B的当前值出发,重新估计A的取值,这个过程一直持续到收敛为止。
-
EM算法还是许多非监督聚类算法的基础(如Cheeseman et al. 1988),而且它是用于学习部分可观察马尔可夫模型(Partially Observable Markov Model)的广泛使用的Baum-Welch前向后向算法的基础。
em算法介绍
-
隐变量:即未观测变量
-
变量定义
- 观测随机变量/不完全数据(不是类标记):Y
- 隐随机变量:Z
- 完全数据:Y+Z
-
给定不完全数据Y,其对数似然函数L(θ)=logP(Y∣θ)
-
隐变量Z可看作中间结果,决定θ,而Y决定Z和θ
-
假设Y和Z的联合概率分布是P(Y,Z∣θ),则完全数据的对数似然函数是logP(Y,Z∣θ)
-
EM算法的目标是通过迭代求L(θ)=logP(Y,Z∣θ)的极大似然估计
em算法整体框架
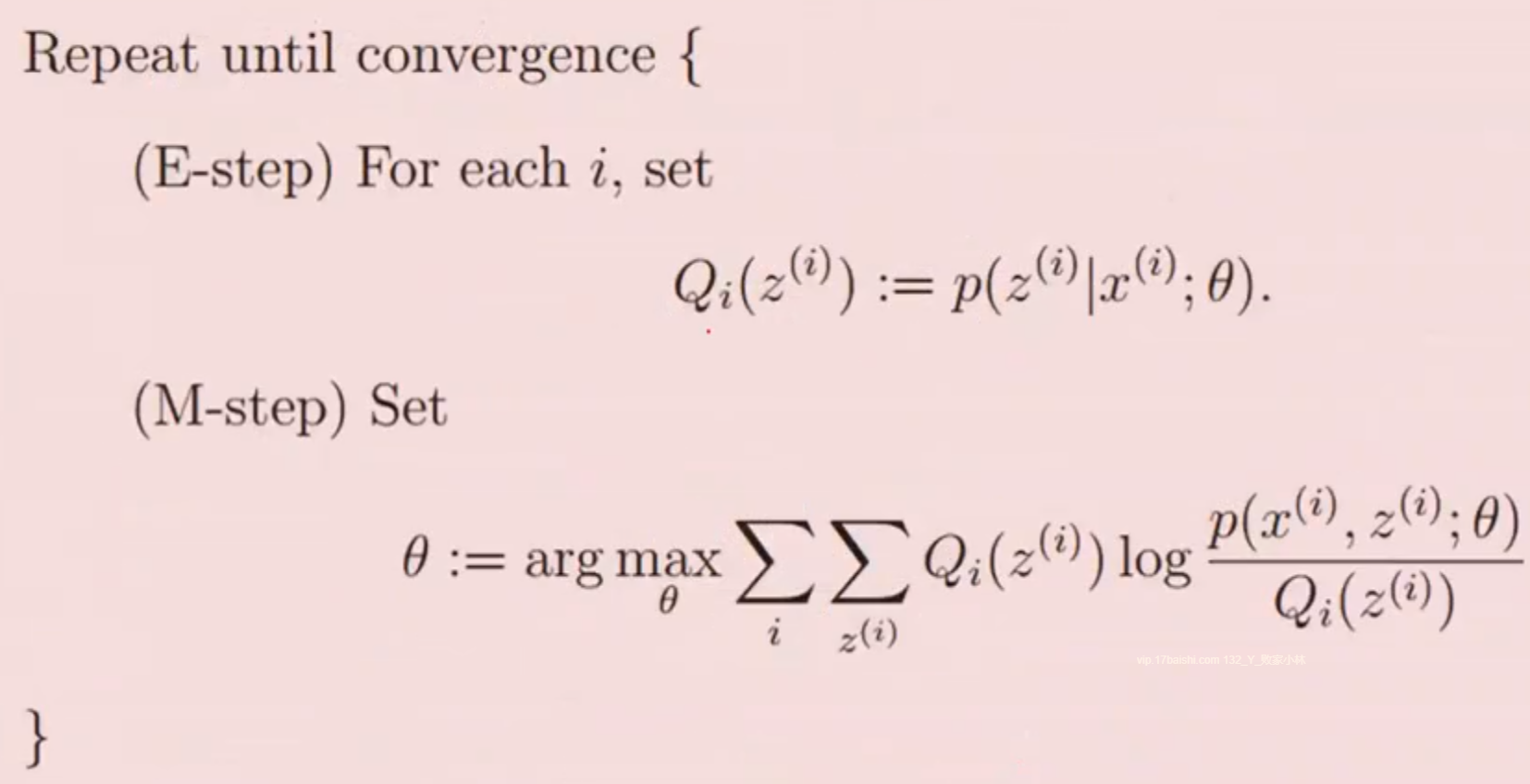
- 坐标上升
![]()
算法说明
-
简单性、 普适性
-
参数初值可任意选择,但要注意算法对初值敏感
-
不能保证找到全局最优值,但能收敛到局部最优值
模型选择的准则




 浙公网安备 33010602011771号
浙公网安备 33010602011771号