课时二、线性回归

最小二乘

使用最大似然估计解释最小二乘

• 中心极限定理（CLT）指出，如果样本量足够大，则变量均值的采样分布将近似于正态分布，而与该变量在总体中的分布无关

• 高斯分布：若连续型随机变量X的概率密度为：\(f\left ( x \right )=\frac{1}{\sqrt{2\pi }\sigma }e^{-\frac{\left ( x-\mu \right )^{2}}{2\sigma ^{2}}}\) , \(-\infty < x< \infty\)

假设

假设的性质： 内涵型、简化性、发散性

最小二乘的参数

线性回归的复杂度惩罚因子

正则项与防止过拟合

L1-norm对梯度的处理

Moore-Penrose广义逆矩阵（伪逆）

• 奇异矩阵是线性代数的概念，就是对应的行列式等于0的矩阵

• 奇异矩阵的判断方法：首先，看这个矩阵是不是方阵（即行数和列数相等的矩阵。若行数和列数不相等，那就谈不上奇异矩阵和非奇异矩阵）。 然后，再看此方阵的行列式|A|是否等于0，若等于0，称矩阵A为奇异矩阵；若不等于0，称矩阵A为非奇异矩阵。 同时，由|A|≠0可知矩阵A可逆，这样可以得出另外一个重要结论:可逆矩阵就是非奇异矩阵，非奇异矩阵也是可逆矩阵。

• n 阶方阵 A 是非奇异方阵的充要条件是 A 可逆，即可逆方阵就是非奇异方阵。

SVD计算矩阵的广义逆

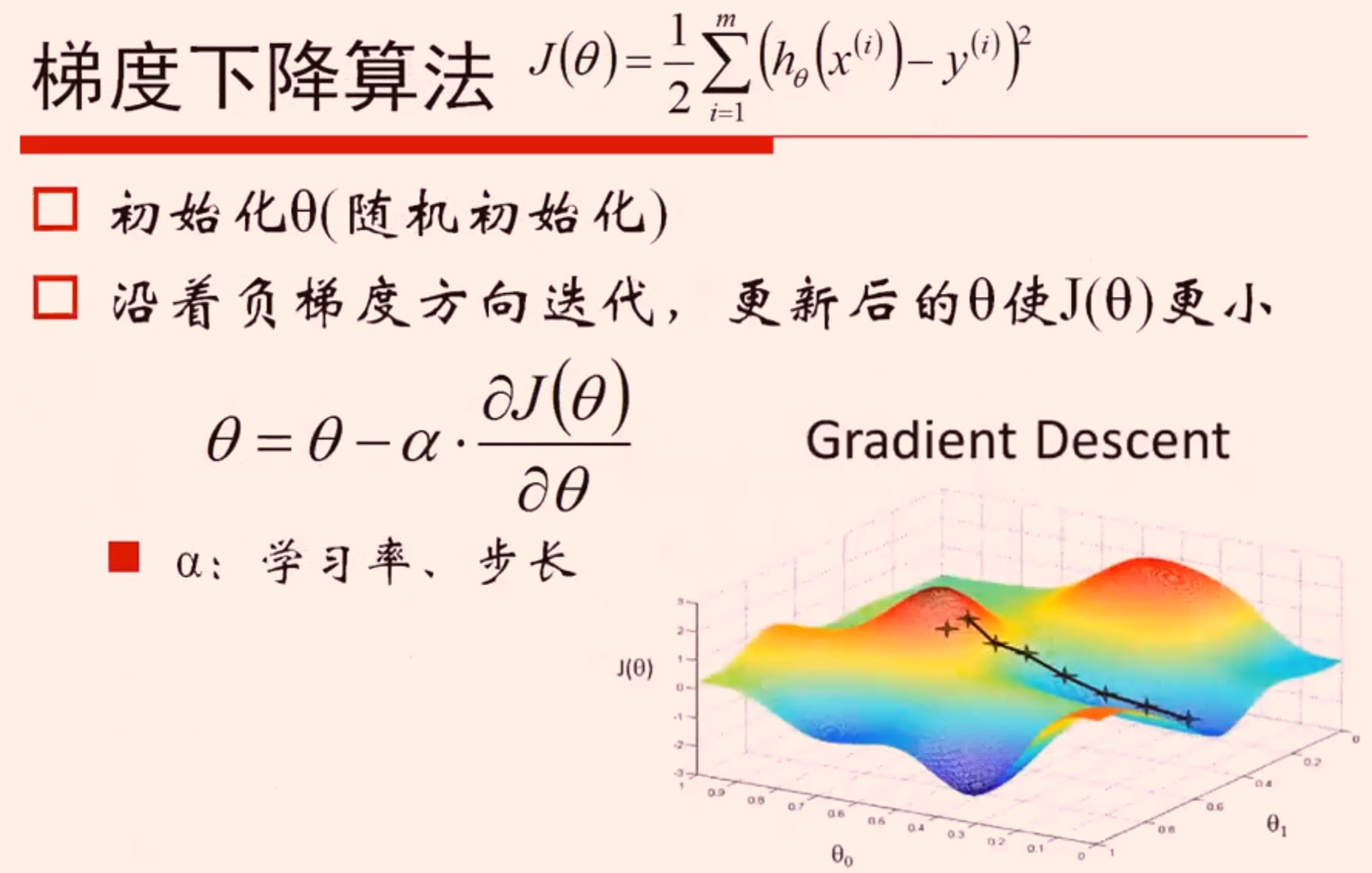
梯度下降算法

• 什么是梯度下降算法

• 使用梯度下降减少误差

批量梯度下降

随机梯度下降

折中：mini-batch（小批量）