图
1.学习总结(2分)
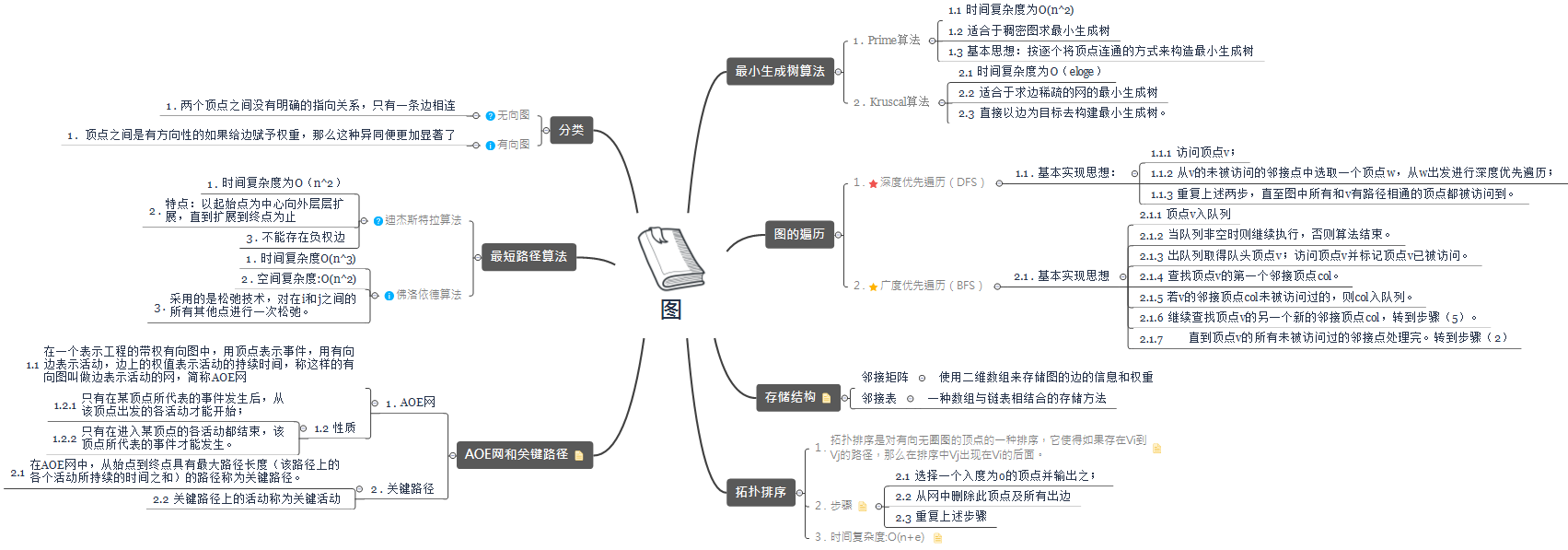
1.1图的思维导图
1.2 图结构学习体会
谈谈你对图结构中的几个经典算法学习体会。具体有：
深度遍历算法：它从图中某个结点v出发，访问此顶点，然后从v的未被访问的邻接点出发深度优先遍历图，直至图中所有和v有路径相通的顶点都被访问到。若图中尚有顶点未被访问，则另选图中一个未曾被访问的顶点作起始点，重复上述过程，直至图中的所有顶点都被访问到为止。
广度遍历算法：它是一个分层搜索的过程和二叉树的层次遍历十分相似，它也需要一个队列以保持遍历过的顶点顺序，以便按出队的顺序再去访问这些顶点的邻接顶点。
Prim算法：普里姆算法是一种构造最小生成树的算法，它是按逐个将顶点连通的方式来构造最小生成树的。
Kruscal算法：克鲁斯卡尔算法是在剩下的所有未选取的边中，找最小边，如果和已选取的边构成回路，则放弃，选取次小边。
Dijkstra算法：Dijkstra算法是典型最短路径算法，用于计算一个节点到其他节点的最短路径。 它的主要特点是以起始点为中心向外层层扩展(广度优先搜索思想)，直到扩展到终点为止
拓扑排序算法：将一个有向无环图进行排序进而得到一个有序的线性序列。
2.PTA实验作业（4分）
2.1 题目1：图着色问题
2.2 设计思路（伪代码或流程图）
建图
for m=0 to n{
for i=0 to v
{
输入颜色并插入s；
num[i] = color;
}
if (颜色数不等于输入值k) {
flag = 0;
}
else {
判断是否符合条件，符合flag=1，不符合0；
}
flag不为0输出yes，否则no
}
2.3 代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）
2.4 PTA提交列表说明。
编译错误：调用memset时没有使用头函数
部分正确：MAXV的值用了6-1的200，不够
2.1 题目2：六度空间
2.2 设计思路（伪代码或流程图）
建图并从v=1开始遍历之
q.push（v）
while（队不空）{
将number置为队列头元素，删除队列头元素；
for i=0 to i=N{
若visited[i]==0且G[number][i]==1；
将i进队，visited[i]=1，tail=i
}
}
if(访问到该层的最后一个节点)
层数++
last = tail;
if(层数==6)
return 节点数
2.3 代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）
2.4 PTA提交列表说明。
编译错误：在头函数中加入了vs的头函数，还有一次是选择的C中用了c++的语法
2.1 题目3：排座位
2.2 设计思路（伪代码或流程图）
建图初始化并输入数据
for i=0 to K
if（是朋友）输出No problem
flag=0判断有无共同;
调用判断函数
if(敌人)
if（有共同） 输出OKBUT
if（无共同） Noway
if(不是朋友)
if(有共同) No problem
if(无共同) OK
2.3 代码截图（注意，截图、截图、截图。代码不要粘贴博客上。不用用···语法去渲染）
2.4 PTA提交列表说明。
段错误：MAXV太大
编译错误：没加头函数
部分正确：查询函数有点问题
3.截图本周题目集的PTA最后排名（3分）
本次题目集总分：310分
3.1 PTA排名（截图带自己名字的排名）
3.2 我的总分：200
本题评分规则：
（3）PTA总分在200--250分：2分（大部分做完2）
4. 阅读代码（必做，1分）
double a[11000];
struct node{
int val;
node *lc;
node *rc;
};
node *create(){
node *p=new node;
p->lc=NULL;
p->rc=NULL;
return p;
}
void Build(node *&p,int ele){
if(p==NULL){
p=create();
p->val=ele;
return ;
}
if(p->val>=ele){
Build(p->rc,ele);
}
else{
Build(p->lc,ele);
}
return ;
}
queue<node *>Q;int n;
int first=0;
int judge(node *p){
if(p){
if(!first){
return 1;
}
else{
return 0;
}
}
else{
first=1;
}
return 1;
}
void solve(node *p){
Q.push(p);
int biao=0;
int flag=0;
while(!Q.empty()){
node *tm=Q.front();
Q.pop();
if(tm==NULL){
return ;
}
if(flag==0)flag=1;
else printf(" ");
printf("%d",tm->val);
if(tm->lc){
Q.push(tm->lc);
}
if(tm->rc){
Q.push(tm->rc);
}
if(!judge(tm->lc)){
biao=1;
}
if(!judge(tm->rc)){
biao=1;
}
}
if(biao==1){
puts("\nNO");
}
else{
puts("\nYES");
}
}
int main(){
cin>>n;
node *root=create();
root=NULL;
for(int i=0;i<n;i++){
int t;
scanf("%d",&t);
Build(root,t);
}
// mid(root);
solve(root);
return 0;
}
该题是通过一个排序二叉树去判断其是否是完全二叉树，首先要弄清楚完全二叉树的特点是：只允许最后一层有空缺结点且空缺在右边，即叶子结点只能在层次最大的两层上出现，对任一结点，如果其右子树的深度为j，则其左子树的深度必为j或j+1。 即度为1的点只有1个或0个。本题按照完全二叉树的特点就行编些，思路是：对于一颗完全二叉树采用广度优先遍历，从根节点开始，入队列，如果队列不为空，循环。遇到第一个没有左儿子或者右儿子的节点，设置标志位，如果之后再遇到有左/右儿子的节点，那么这不是一颗完全二叉树。这个方法需要遍历整棵树，复杂度为O(N)，N为节点的总数。
