【学习笔记】数学
数学
大概就是一个数学知识的梳理，可能会有一些地方写的并不是很全很好，未来可能会补。
模意义下的数论
欧几里得算法
扩展欧几里得算法
求解：
分析：
设 \(ax_1 + by_1 = \gcd(a,b)\)，\(bx_2 + (a\%b)y_2 = \gcd(b,a\%b)\)。
根据欧几里得算法则 \(\gcd(a,b) = \gcd(b,a\%b)\)，也就是说：
根据 \(a \% b = a - \lfloor \frac{a}{b} \rfloor \times b\)，则有：
化简一下就有：
必然存在一组解为 \(x_1 = y_2,y_1 = x_2 - \lfloor \frac{a}{b} \rfloor \times b \times y_2\)
不断递归下去，当 \(b = 0\) 时使用 \(x=1,y=0\) 作为一组解然后回溯即可。
费马小定理
对于素数 \(p\)，若 \(\gcd(a,p) = 1\)，则有：
欧拉定理
若 \(\gcd(a,p) = 1\)，则有：
扩展欧拉定理
中国剩余定理
问题描述：
求一组解：
其实满足 \(m_1,m_2,\cdots,m_n\) 两两互质
问题分析：
令 \(M = \prod_{i=1}^n a_i\)。
对于第 \(i\) 个方程，令 \(p_i = \frac{M}{m_i}\)，计算 \(p_i\) 在模 \(m_i\) 意义下的逆元 \(p_i^{-1}\)，令 \(c_i = p_ip_i^{-1}\)（不对 \(m_i\) 取模）。
则答案为 \(x = \sum_{i=1}^n c_ia_i \mod M\)
扩展中国剩余定理
考虑合并两个方程：
可以将它们转化为不定方程即：
转化一下即 \(m_1p - m_2q = a_2 - a_1\)，根据裴蜀定理当 \(a_2 - a_1\) 不能被 \(m_1 - m_2\) 整除时无解，否则可以通过扩展欧几里得算法得到一组解 \(p,q\)。
这样的话就可以将原方程组合并为：\(x \equiv b \mod M\)，其中 \(b = m_1p + a_1，M = \text{lcm}(m_1,m_2)\)
Wilson 定理
\(p\) 为素数的充要条件为 \((p-1)! \equiv -1 \mod p\)
Kummer 定理
形式一：\(p\) 在 \(\binom{n}{m}\) 中的幂次，等于 \(p\) 进制下 \(n - m\) 需要的借位次数
形式二：\(p\) 在 \(\binom{n+m}{m}\) 中的幂次，等于 \(p\) 进制下 \(n+m\) 的进位次数
Lucas 定理
若有两个正整数 \(n,m\) 和一个素数 \(p\)，则有：
感性的理解就是拆到 \(p\) 进制下，然后每一位单独考虑。
阶
定义： 对于 \(a \in \mathbb{Z}，m \in \mathbb{N}^*\)，若 \((a,m) = 1\)，则满足 \(a^n \equiv 1 \pmod m\) 的最小正整数 \(n\) 称为 \(a\) 模 \(m\) 的阶，记为 \(\delta_m(a)\) 或 \(\text{ord}_m(a)\)。
性质一： \(a^1,a^2,\cdots,a^{\delta_m(a)}\) 模 \(m\) 两两不同余。
- 证明：考虑使用反证法，若存在 \(i \not= j\) 满足 \(a^i \equiv a^j \pmod m\)，则必然有 \(a^{|i-j|} \equiv 1 \pmod m\)，而 \(0 < |i-j| < \delta_m(a)\) 与定义冲突。
性质二： 若 \(a^n \equiv 1 \pmod m\)，则必然有 \(\delta_m(a) | n\)。以及据此可以推出若 \(a^p \equiv a^q\)，则 \(p \equiv q \pmod{\delta_m(a)}\)
性质三： \(\delta_m(ab) = \delta_m(a) \delta_m(b)\) 的充要条件为 \((\delta_m(a),\delta_m(b)) = 1\)。
性质四： \(\delta_m(a^k) = \dfrac{\delta_m(a)}{(\delta_m(a),k)}\)
所以根据上面这些性质，阶就给了人一种“循环节”的感觉。
原根
若 \(\delta_m(g) = \varphi(m)\)，则称 \(g\) 为模 \(m\) 意义下的原根。
性质一： \(g\) 是模 \(m\) 意义下的原根的充要条件为，对于 \(\varphi(m)\) 的每个质因数 \(p\)，都有 \(g^{\frac{\varphi(m)}{p}} \not\equiv 1 \pmod m\)
性质二： 若模 \(m\) 意义下有原根，则原根个数为 \(\varphi(\varphi(m))\)
性质三： 数 \(m\) 存在原根当且仅当 \(m = 2,4,p^{\alpha},2p^{\alpha}\)，其中 \(p\) 为奇质数，\(\alpha \in \mathbb{N}^*\)
性质四： 最小原根的值为 \(O(n^{0.25})\)，可以暴力。
BSGS
满足 \((a,p) = 1\)，求解下列方程的解：
考虑按 \(t\) 分块，也就是将上述式子改写为：
移一下项也就是：
所以就可以直接预处理 \(a^0,a^1,\cdots,a^{t-1}\)，然后枚举 \(i\)，通过 hash 判断预处理的数里面是否存在 \(b \times a^{-it}\) 即可。
显然当 \(t = \sqrt{p}\) 时复杂度最优，为 \(O(\sqrt{p})\)。
exBSGS
不满足 \((a,p) = 1\)，求解下列方程的解：
想法就是将这个方程转化为 \((a,p) = 1\)。
首先这个方程显然可以转化为：
设 \((a,p) = d\)，根据裴蜀定理这个式子有解当且仅当 \(d \mid b\)，所以不合法直接判无解。
这样的话这个式子就可以转化为：
此时可以令 \(a^{x-1} \to a^x,\frac{p}{d} \to p,\frac{b}{d} \to b\)，这样一直递归下去，直到 \((a,p) = 1\)。
设总共递归了 \(cnt\) 次，递归过程中 \(d\) 的乘积为 \(d'\)，则显然原式为：
此时直接令 \(a' = a,b' = \frac{b}{d'},p'= \frac{p}{d'}\)，跑一遍 BSGS 然后将答案加 \(cnt\) 即可。
要注意此时左边式子会多一个 \(\frac{a_{cnt}}{d'}\) 的系数，要记得乘上。
二次剩余
定义：
若 \(p\) 为奇质数，且 \((n,p) = 1\)，使得存在一个 \(x\) 满足：
则称 \(n\) 为模 \(p\) 意义下的二次剩余，简称二次剩余，默认 \(n \ge 1\)。（顾名思义就是二次方后剩余的数）
二次剩余的数量：
考虑对于一个二次剩余 \(n\)，考虑 \(x^2 \equiv n \pmod p\) 有多少个解。
若存在多个解，设其中两个解为 \(x_0,x_1\) 且满足 \(x_0 \not= x_1\)，则有：
化简一下就是：
因为 \(x_0 \not= x_1\)，所以 \(x_0 - x_1 \not= 0\)，即要让上述式子为 \(0\) 则必然存在 \(x_0 + x_1 = 0\pmod p\)
也就是模 \(p\) 意义下的一对相反数对应一个二次剩余，因为 \(p\) 为奇质数所以任意一对 \(x_0,x_1\) 若满足 \(x_0 + x_1 = 0\)，则必然满足 \(x_0 \not= x_1\)，也就是说任意一对相反数都可以对应一个二次剩余。
还可以知道的是任意两对相反数所对应的两个二次剩余均不同，所以二次剩余的数量就是 \(\frac{p-1}{2}\)，故非二次剩余的数量就是 \(\frac{p-1}{2}\)
欧拉准则：
考虑怎么快速判断一个数 \(n\) 是不是二次剩余。
考虑费马小定理，\(n^{p-1} \equiv 1 \pmod p\)，因为 \(p\) 为奇质数，所以有 \(n^{2\cdot \frac{p-1}{2} } \equiv 1 \pmod p\)，也就是说 \(n^{\frac{p-1}{2}}\) 是 \(1\) 的开根，因为 \(1\) 的开根只有 \(1\) 或 \(-1\)，所以 \(n^{\frac{p-1}{2}}\) 只可以为 \(1\) 或者 \(-1\)。
下面考虑证明 \(n^{\frac{p-1}{2}} \equiv 1 \pmod p\) 与 \(n\) 为二次剩余等价，也就是证明充分性和必要性。
充分性，也就是已知 \(n^{\frac{p-1}{2}} \equiv 1 \pmod p\)，设 \(g\) 表示模 \(p\) 意义下的原根，则可以令 \(n = g^k\)，则有 \(g^{k\cdot \frac{p-1}{2}} \equiv 1 \pmod p\)，有原根的性质可得 \((p-1) \mid k\cdot \frac{p-1}{2}\)，也就是说 \(k\) 一定是偶数，即我们可以将 \(k\) 除以 \(2\)，所以 \(n\) 就是可以开根的，开根后的结果就是 \(x = g^{\frac{k}{2}}\)
必要性，也就是已知 \(n\) 是二次剩余，\(n^{\frac{p-1}{2}} = (x^2)^{\frac{p-1}{2}} = x^{p-1}\)，因为 \(x^{\varphi(p)} \equiv 1 \pmod p\)，所以 \(x^{p-1} \equiv 1 \pmod p\)，即 \(n^{\frac{p-1}{2}} \equiv 1 \pmod p\)
所以就证明了 \(n^{\frac{p-1}{2}} \equiv 1 \pmod p\) 与 \(n\) 为二次剩余等价，所以当 \(n^{\frac{p-1}{2}} \equiv -1 \pmod p\) 时 \(n\) 就是非二次剩余。
Cipolla：
考虑求解 \(x^2 \equiv n \pmod p\)
首先找到一个 \(a\) 使得 \(a^2 - n\) 是非二次剩余，因为非二次剩余的数的个数接近 \(\frac{p}{2}\) 所以期望两次找到。
定义 \(i^2 = a^2 - n\)，下面就是关于怎么找到这个 \(i\)。
可以类似复数域，定义这样的一个 \(i\)，使得每一个数都可以被表示为 \(A + Bi\)，其中 \(A,B\) 都是模 \(p\) 意义下的。
下面考虑证明下面这个结论：
引理 \(1\)： \(i^p \equiv -i \pmod p\)
- 证明：\(i^p = i(i^2)^{\frac{p-1}{2}} = i(a^2 - n)^{\frac{p-1}{2}} = -i\)
引理 \(2\)： \((A+B)^p \equiv A^p + B^p \pmod p\)
- 证明：\((A+B)^p \equiv \sum_{i=0}^p \binom{p}{i} A^iB^{p-i} \equiv \binom{p}{p} A^p + \binom{p}{0}B^p \equiv A^p + B^p \pmod p\)
有了这两个引理就可以证明了：
第二个等于号 \(a^p \equiv a \pmod p\) 就是扩展欧拉定理。
因为 \(p\) 为奇质数，所以 \(p+1\) 为偶数，因此 \(n\) 开方后的数就是 \((a+i)^{\frac{p+1}{2}}\)，即 \(x\) 就是 \((a+i)^{\frac{p+1}{2}}\)
可以证明 \((a+i)^{\frac{p+1}{2}}\) 的 “虚部” 一定为 \(0\)。
使用反证法来证明这个结论，若存在 \((A+Bi)^2 \equiv n \pmod p\) 且 \(B \not= 0\)，那么展开之后就是 \(A^2 + B^2i^2 + 2ABi \equiv n \pmod p\)，因为右边"虚部"为 \(0\) 所以显然左边"虚部"为 \(0\)，即 \(AB = 0\)，因为 \(B \not= 0\)，所以 \(A = 0\)，上面式子就可以化为 \(B^2i^2 \equiv n \pmod p\)，即 \(i^2 \equiv nB^{-2} \pmod p\)，显然 \(B^{-2}\) 是一个二次剩余，而 \(n\) 也是一个二次剩余，所以 \(nB^{-2}\) 就是一个二次剩余，即 \(i^2\) 是一个二次剩余，这与我们的假设 \(i^2\) 不是一个二次剩余违背，故此这个结论不成立。
正整数中的数论
算术基本定理
内容： 对于任意一个大于 \(1\) 的自然数 \(N\)，其一定可以被唯一分解为有限个质数的乘积。
标准分解式： \(N = \prod_{i=1}^m p_i^{k_i}\)，满足 \(p_1 < p_2 < p_3 \cdots < p_m\) 且 \(p_1,p_2,p_3,\cdots,p_m\) 均为质数，\(k_i\) 均为正整数，将这样的分解称为 \(N\) 的标准分解式。
p 进赋值序列： 记 \(v_p(n) = \max\{k \in \mathbb{n}\mid p^k \mid n\}\)，则 \(n\) 的 \(p\) 进赋值序列为 \(\{v_2(n),v_3(n),v_5(n),v_7(n),\cdots\}\)，即要求 \(p\) 均为质数。
\(p\) 进赋值序列可以帮助我们在数论的角度下刻画正整数，在 \(p\) 进赋值序列下任何一个正整数都唯一对应一个高维平面上的点，该平面每一维对应一个素数。
\(\gcd\) 与 \(\text{lcm}\) 就可以转化为高维平面上的 \(\min\) 与 \(\max\)。
狄利克雷前缀和就对应高维前缀和，狄利克雷卷积就对应着高维和卷积。
莫比乌斯函数相当于高维差分的容斥系数。
素性检测和因数分解
素性检测就是在不对给定数进行质因数分解的情况下判断这个数是否为质数。
Miller–Rabin 素性测试
引理一：费马小定理
若 \(p\) 为素数，\(a\) 为整数，若 \((a,p) = 1\)，则有 \(a^{p-1} \equiv 1 \pmod p\)
费马小定理只是 \(p\) 为素数的充分条件，如不成立则 \(p\) 一定为合数，若成立则 \(p\) 不一定为素数。
引理二：二次检测定理
若 \(p\) 为素数，且 \(0 < x < p\)，则 \(x^2 \equiv 1 \pmod p\) 的解为 \(x=1\) 或 \(x=p-1\)
证明：
\(x^2 \equiv 1 \pmod p \Longrightarrow x^2 - 1 \equiv 0 \pmod p \Longrightarrow (x+1)(x-1) \equiv 0 \pmod p \Longrightarrow p \mid (x+1)(x-1)\)。
因为 \(p\) 为质数，所以只有 \(x = 1\) 或 \(x = p-1\)。
下面考虑给定 \(p\) 判断其是否为素数。
我们将 \(p-1\) 写成 \(2^k \times t\) 的形式，可以考虑随机一个数 \(a\)，然后计算 \(a^t \pmod p\) 的值。
将这个数不断自乘，然后使用二次检测定理判断，也就是若当前的数为 \(A\) 满足 \(A \times A = 1\) 且 \(A \not= 1\) 且 \(A \not= p-1\)，则 \(p\) 不是素数。
这样乘 \(k\) 次的结果就是 \(a^{p-1}\)，这个时候只需要判断 \(a^{p-1} \equiv 1 \pmod p\) 是否满足即可，如果不满足则一定不是素数。
这样检测的正确率是不低的，可以验证的是如果我们取前 \(12\) 个素数作为 \(a\) 进行检测则在 \([1,2^{64})\) 内的数都不会出现问题。
时间复杂度就是 \(O(|a|log^3n)\)
代码实现如下：
点击查看代码
bool Miller(int P) {
if(P == 1) return 0;
int t = P - 1, k = 0;
while(!(t & 1)) k++, t >>= 1;
for(int i = 0; i < 12; i++) {
if(P == Test[i]) return 1;
LL a = pow(Test[i], t, P), nxt = a;
for(int j = 1; j <= k; j++) {
nxt = (a * a) % P;
if(nxt == 1 && a != 1 && a != P - 1) return 0;
a = nxt;
}
if(a != 1) return 0;
}
return 1;
}
Pollard-Rho 算法
首先要明确这个算法的功能就是在 \(O(n^{\frac{1}{4}})\) 的时间内找到数 \(n\) 的一个因子。
一个暴力的想法就是我们每次随机一个数，判断这个数是不是因子，如果是就返回如果不是就继续随机，但是这样的复杂度就炸了。
考虑构造如下的随机数序列：
定义 \(f(x) = (x^2 + c) \pmod N\)，那么我们构造的随机数序列就是 \(x,f(x),f(f(x)),\cdots\)。
这个序列的样子大概就是下面这个样子：
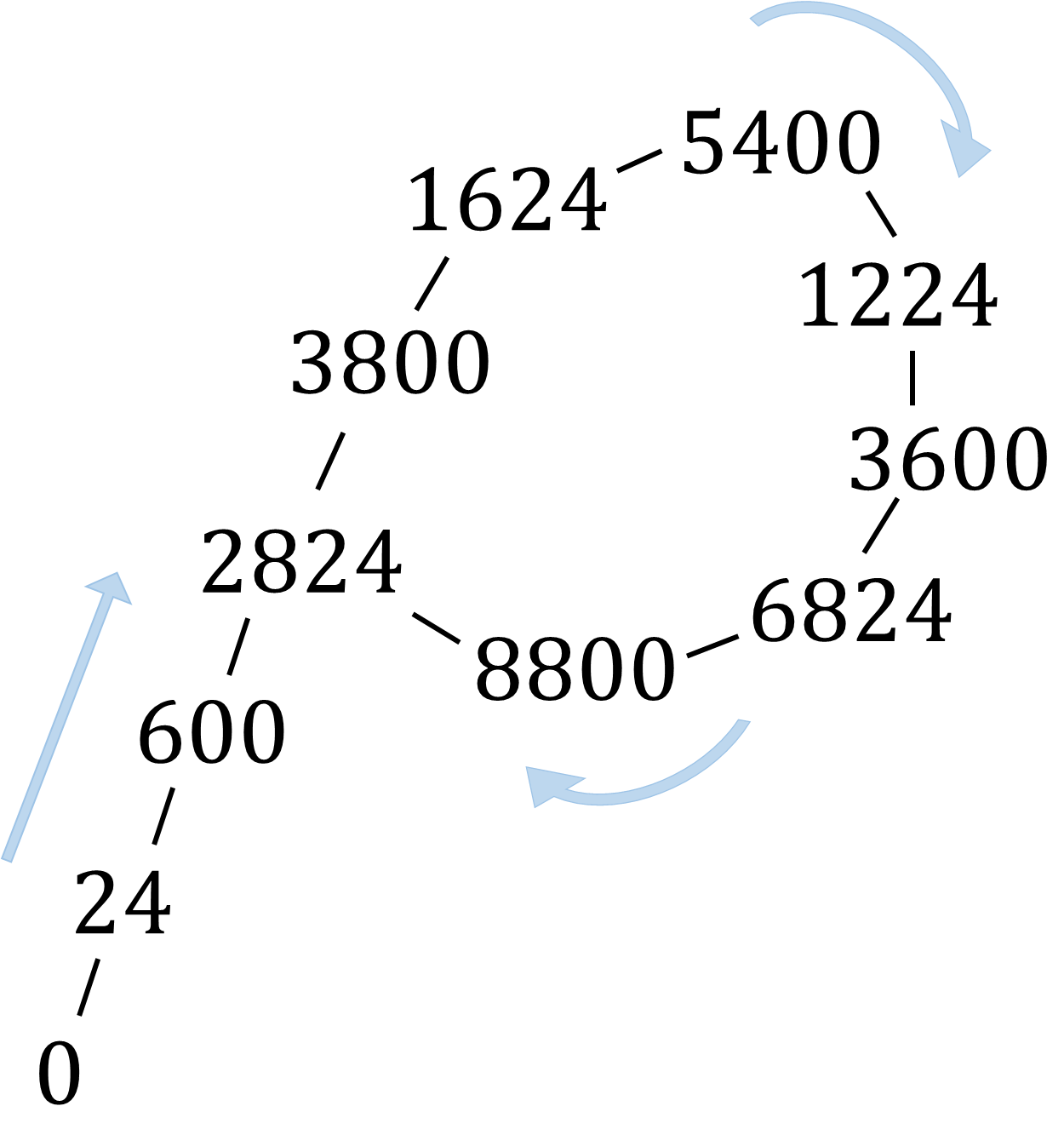
也就是一个 \(\rho\) 的形状，而根据生日悖论期望随机 \(O(n^{\frac{1}{4}})\) 个数可以找到相同的数，所以这里期望环长为 \(O(n^{\frac{1}{4}})\)。
那么如果快速判环，可以使用类似龟兔赛跑的算法，也就是设置两个变量 \(t,r\)，每次判断是否有 \(gcd(|t-r|,n) \not= 1\) 且 \(gcd(|t-r|,n) \not= n\)，若有则 \(|t-r|\) 就是 \(n\) 的一个因数，如果没有我们就令 \(t = f(t),r=f(f(r))\)，可以发现这样的话 \(r\) 比 \(t\) 跑的快也就是它们在环上一定可以相遇。
这个时候就能体现出我们这个随机序列的优势了：
若 \(|i-j| \equiv 0 \pmod p\)，则有 \(|f_i - f_j| = (i^2 - j^2) = (i-j)(i+j) \equiv 0 \pmod p\)，所以我们只需要对两个点之间的距离 \(d\) 进行判断就好，不在于哪两个点而在于他们的距离，而我们上面的龟兔赛跑也显然是枚举到了每一种距离。
直接这样做就是 \(O(n^{\frac{1}{4}}\log n)\)。
优化就是减小求 \(gcd\) 的次数，可以考虑设一个固定的距离 \(C\) 然后每隔 \(C\) 个求一个公因数然后判断，这样的话期望的时间复杂度就是 \(O(n^\frac{1}{4})\)。
代码实现：
点击查看代码
ll Pollard_Rho(ll N)
{
if (N == 4)
return 2;
if (is_prime(N))
return N;
while (1)
{
ll c = randint(1, N - 1);
auto f = [=](ll x) { return ((lll)x * x + c) % N; };
ll t = 0, r = 0, p = 1, q;
do
{
for (int i = 0; i < 128; ++i) // 令固定距离C=128
{
t = f(t), r = f(f(r));
if (t == r || (q = (lll)p * abs(t - r) % N) == 0) // 如果发现环，或者积即将为0，退出
break;
p = q;
}
ll d = gcd(p, N);
if (d > 1)
return d;
} while (t != r);
}
}
数论函数和筛法
此处可以查看如下几篇 blog，推荐按顺序观看：
本文只在此基础上补充几个知识点。
区间筛
给定区间 \([l,r]\) 要求区间 \([l,r]\) 中的素数的数量。
考虑若 \(x \le r\) 且 \(x\) 不为素数，则 \(x\) 必然拥有一个小于等于 \(\sqrt{r}\) 的质因子，所以只需要用 \([2,\sqrt{r}]\) 筛一遍区间 \([l,r]\) 留下来的就是素数。
一些小 tip
\(a \mod b = a - a\times \lfloor \frac{a}{b} \rfloor\)
\(\lfloor {\frac{\lfloor\frac{a}{b}\rfloor}{c}} \rfloor = \lfloor {\frac{a}{bc}} \rfloor\)
整除分块中如果式子中多个数整除，复杂度是加而不是乘。
集合幂级数
FWT 与 FMT
FWT 与 FMT 是解决如下问题的工具：
其中 \(\oplus\) 为二进制下的 and or xor 三种运算之一。
下面将 FWT 与 FMT 统称为 FWT。
其解决这个问题的思路也类似 FFT，就是将序列 \(a,b\) 转化为某种变换 \(\text{FWT}(a),\text{FWT}(b)\) 然后乘起来得到 \(\text{FWT}(c)\) 后反演得到 \(c\)。
OR
要求：
考虑若 \(i \mid k = k\) 且 \(j \mid k = k\) 则 \((i\mid j) \mid k = k\)，就使用这个来设计变换。
即 \(\text{FWT}_{or}(A)_k = \sum_{i\mid k = k} A_i\)
也就是 \(i\) 为 \(k\) 的子集才可以转移。
那考虑为什么这样是对的：
所以这个变换就是正确的。
那么考虑如何快速进行这个变换，类似 FFT 每次合并两个长度为 \(2^n\) 的段，设不同的最高位为 \(1\) 的序列为 \(A_1\)，为 \(0\) 的序列为 \(A_0\)，则根据 \(or\) 的性质 \(A_0\) 可以转移到 \(A_1\)，而 \(A_1\) 不能转移到 \(A_0\)，也就是形如下面这样：
其中 \(A + B\) 是对应系数相加，\((A,B)\) 就是按顺序写下 \(A,B\)。
逆变换就是逆着做这个操作就好了，即：
代码：
点击查看代码
void Or(ll *x,int n,int op){
for(int l=1;l<n;l<<=1){
for(int st=0;st<n;st+=l*2){
for(int i=0;i<l;i++){
ll u=x[st+i],v=x[st+l+i];
if(op==1) x[st+i]=u,x[st+l+i]=(v+u)%mod;
else x[st+i]=u,x[st+l+i]=(v+mod-u)%mod;
}
}
}
}
AND
要求：
考虑若 \(i \& k = k\) 且 \(j \& k = k\) 则 \((i\&j) \& k = k\)，所以可以构造如下的变换：\(\text{FWT}_{and}(A)_k = \sum_{i\&k=k} A_i\)
也就是 \(i\) 为 \(k\) 的超集时产生贡献。
变化的与上文同理：
代码：
点击查看代码
void And(ll *x,int n,int op){
for(int l=1;l<n;l<<=1){
for(int st=0;st<n;st+=l*2){
for(int i=0;i<l;i++){
ll u=x[st+i],v=x[st+l+i];
if(op==1) x[st+i]=(u+v)%mod,x[st+l+i]=v;
else x[st+i]=(u+mod-v)%mod,x[st+l+i]=v;
}
}
}
}
XOR
要求：
设 \(d(x)\) 表示二进制下 \(x\) 的 \(1\) 的个数的奇偶性，则有如下性质：\(d(i\&k)\oplus d(j\&k) = d((i\oplus j) \& k)\)。
证明：因为我们是与操作，所以可以只考虑 \(k\) 为 \(1\) 的位。若某一位上 \(i,j\) 同时为 \(0\) 或 \(1\) 则显然不会有什么影响，若某一位上 \(i,j\) 分别为 \(0,1\) 那么左右两边都是同步变化的，所有也是一样的。
所以可以设计出以下的变换：
可以乘一下看看是不是对的：
这样就形式化对了，所以这个就是正确的。
考虑怎么快速求解，其实就是新加一位，而新加一位只有 \(1\) 贡献到 \(1\) 会导致奇偶性改变，也就是取负，其它的都没有变化。
即：
逆变换其实就是考虑 \(A_0,A_1\) 已经变成上面那个东西了，怎么还原回来的，就是：
代码：
点击查看代码
void Xor(ll *x,int n,int op){
for(int l=1;l<n;l<<=1){
for(int st=0;st<n;st+=l*2){
for(int i=0;i<l;i++){
ll u=x[st+i],v=x[st+l+i];
if(op==1) x[st+i]=(u+v)%mod,x[st+l+i]=(u+mod-v)%mod;
else x[st+i]=(u+v)%mod*inv2%mod,x[st+l+i]=(u+mod-v)%mod*inv2%mod;
}
}
}
}
FWT 的一些性质
FWT 的本质是一个线性变换，也就是：
\(\text{FWT}(A+B) = \text{FWT}(A) + \text{FWT}(B)\)，\(\text{FWT}(cA) = c\text{FWT}(A)\)
集合幂级数
位运算是 OI 中的常考知识点，因为位运算中每一位的独立性，所以可以将其看作两个 \(\{0,1\}^n\) 上的向量的运算。
生成函数是刻画序列的有力工具，而集合幂级数就是处理集合（位运算）的一种特殊形式。对于序列 \(a_0,a_1,\cdots,a_{2^n-1}\) 我们可以定义其集合幂级数 \(A(x) = \sum \limits_{i=0}^{2^n-1}a_ix^i\)。
定义集合幂级数的乘法操作，也就是子集卷积为如下的形式；
组合意义就是选择两个不交的集合，可以直接枚举子集就可以做到 \(O(3^n)\)。
可以构造占位函数 \(w(x) = \text{popcount}(x)\)，这样上述条件可以等价为 \(j \ \text{xor} \ k = i\) 且 \(w(j) + w(k) = w(i)\)，这样就可以以 \(w(x)\) 来构造一个二元集合幂级数 \(A(x,y) = \sum \limits_{i=0}^{2^n-1} a_ix^iy^{w(i)}\)，而子集卷积就相当于对于第一维异或卷积，第二维和卷积，都是可以做的，所以就可以一维维来做，时间复杂度 \(O(n^22^n)\)。
因为不出意外的话我们第二维都为 \(O(\log n)\) 级别，所以直接暴力做和卷积就没问题，不用再写 FFT 了。
代码：
点击查看代码
int main()
{
m=read();n=(1<<m);
for (int i=1;i<n;i++)c[i]=c[i>>1]+(i&1);
for (int i=0;i<n;i++)F[i].a[c[i]]=read();
for (int i=0;i<n;i++)G[i].a[c[i]]=read();
FWT(F,n);FWT(G,n);
for (int i=0;i<n;i++)
F[i]=F[i]*G[i];
IFWT(F,n);
for (int i=0;i<n;i++)
printf("%d ",(F[i].a[c[i]]+mod)%mod);
return 0;
}
这个技巧就被称为占位多项式，有了这个占位多项式我们就可以对集合幂级数做各种多项式的操作，但是那东西我完全不会，就不说了。
组合计数
计数原理
加法原理： 若完成某道工序有两种方法，第一种方法的实现方式有 \(a\) 种，第二种方法的实现方式有 \(b\) 种，则完成这道工序的实现方法有 \(a+b\) 种。
乘法原理： 若完成某道工序有两个步骤，第一个步骤有 \(a\) 种实现方式，第二个步骤有 \(b\) 种实现方式，则完成这道工序的实现方法有 \(ab\) 种。
其实只需要观察它们是不是相互独立的就可以判断出应使用加法原理还是乘法原理。
算两次原理（富比尼原理）： 将同一个量同两个不同角度计算两次，从而建立等量关系。
这东西看上去很玄乎，但是其实放在 OI 中就是：维度的变换（枚举下标/权值）、贡献的计算（直接计算/增量计算）等，从不同的角度解决问题，并在选取了合适的角度之后通过其它的方法解决问题。
例题 P8557 炼金术：
有 \(k\) 个熔炉，每个熔炉可以随机炼出 \(n\) 种金属中的一些，当 \(n\) 种金属都被炼制出来过该方案就是合法的，询问有多少种合法的方案。
考虑按每一种金属考虑，其在每一个熔炉中都可以出现或者不出现，所以方案数为 \(2\)，而其在 \(k\) 个熔炉中出现的情况相互独立，所以方案数为 \(2^k\)，但是这个金属必须要在某一个熔炉中出现，所以真实的方案数为 \(2^k-1\)。
对于不同的金属之间相互独立，所以总方案数为 \((2^k-1)^n\)。
鸽巢原理： \(n\) 个小球放到 \(m\) 个抽屉中，至少有一个抽屉放了大于等于 \(\lceil \frac{n}{m} \rceil\) 个。
这个原理常用于结论的证明，以及一些极端情况的求解等。
组合数
组合数的计算
递推形式：\(\binom{n}{m} = \binom{n-1}{m} + \binom{n-1}{m-1}\)。
阶乘形式：\(\binom{n}{m} = \frac{n!}{m!(n-m)!} = \frac{n^{\underline{m}}}{m!}\)
Lucas 定理：\(\binom{n}{m} = \binom{n \mod p}{m \mod p} \times \binom{\lfloor \frac{n}{p} \rfloor}{\lfloor \frac{m}{p} \rfloor}\)
组合恒等式：
- 吸收恒等式： \(\binom{n}{m} = \frac{n}{m} \binom{n-1}{m-1}\)，移项得 \(m\binom{n}{m} = n\binom{n-1}{m-1}\)
证明：根据组合数的阶乘形式易得 - 行求和：\(\sum_{i=0}^n \binom{n}{i} = 2^n\)
证明：根据二项式定理 \((1+1)^n = \sum_{i=0}^n \binom{n}{i} = 2^n\) - 列求和：\(\sum_{i=n}^m \binom{i}{n} = \binom{m+1}{n+1}\)
证明：\(\binom{n}{n} + \binom{n+1}{n} + \binom{n+2}{n} + \cdots + \binom{m}{n} = \binom{n+1}{n+1} + \binom{n+1}{n} + \binom{n+2}{n} + \cdots + \binom{m}{n} = \binom{n+2}{n+1} + \binom{n+2}{n} + \cdots + \binom{m}{n} = \binom{m}{n+1} + \binom{m}{n} = \binom{m+1}{n+1}\)，主要是使用了组合数的递推形式。 - 范德蒙德卷积：\(\sum_{i=0}^k \binom{n}{i}\times\binom{m}{k-i} = \binom{n+m}{k}\)
证明：考虑我们枚举的其实就是 \(n\) 个里面选 \(i\) 个和 \(m\) 个里面选 \(k-i\) 个，显然可以合并起来。
组合数的应用：
隔板法：\(n\) 个相同的小球放到 \(m\) 个不同的盒子里，每个盒子里必须至少放一个小球，方案数为 \(\binom{n-1}{m-1}\)。
证明：考虑将 \(n\) 个小球放到一排，这样中间就出现了 \(n-1\) 个缝隙，放到 \(k\) 个不同的盒子中相当于划分为 \(k\) 段也就是选择 \(k-1\) 个缝隙放上隔板，方案数就是 \(\binom{n-1}{m-1}\)。
扩展： 如果将要求改为每个盒子可以不放小球，那么方案数就是 \(\binom{n+m-1}{m-1}\)，可以理解为先将所有的盒子提前放上一个小球，这样就必须至少放 \(1\) 个了。
捆绑法：有 \(n\) 个不同的人站队，要求其中两个人必须相邻，方案数为 \((n-1)! \times 2!\)。
证明：将这两个人视为一个人去站队方案数为 \((n-1)!\)，而两个人内部也可以随便站方案数为 \(2!\)。
格路计数：给定一个 \(n \times m\) 的网格，每次可以从 \((x,y)\) 走到 \((x+1,y)\) 或者 \((x,y+1)\)，从 \((1,1)\) 走到 \((n,m)\) 的方案数为 \(\binom{n+m}{n}\)。
证明：我们总共要走 \(n+m\) 步才能走到 \((n,m)\) 这其中有 \(n\) 步是执行 \((x,y) \to (x+1,y)\)，而且这 \(n\) 步可以在任意位置。
卡特兰数：见数论之生成函数基础。
prufer 序列
对于一棵有 \(n\) 个节点的带标号树，其 prufer 序列一定是一个长度为 \(n-2\) 值域为 \([1,n]\) 的序列。
树转化为 prufer 序列：
- 选择树上编号最小的叶子节点，将其父亲插入到序列的末尾
- 删除这个选择的叶子节点
- 重复上述步骤直到树中只剩下两个节点
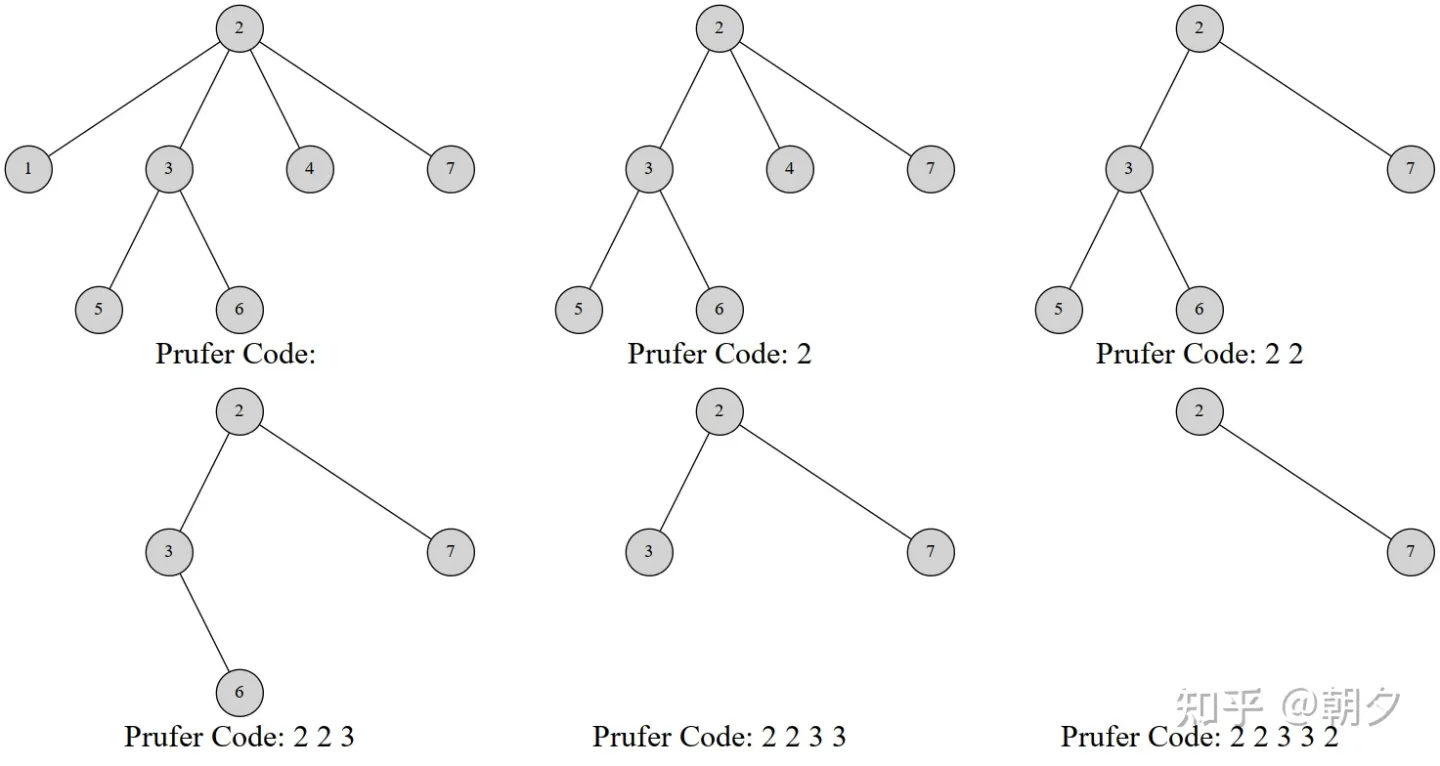
注意到我们的 prufer 序列与树构成一个双射，所以我们可以由 prufer 序列还原对应的树。
- 选择编号最小的一个叶子节点（即从未在序列中出现的点），其父亲就是序列第 \(i\) 个数。（\(i\) 初始为 \(1\)）
- 点 \(x\) 的度数为 \(x\) 的出现次数加 \(1\)，所以可以删除这个叶子节点，然后将其父亲的度数减 \(1\)，直到其父亲度数变为 \(1\) 就成为了叶子节点。
- 重复上述两步，直到序列全部被用完。
可以发现这样构造出的 prufer 序列有如下的性质：
- 剩下的两个节点中，一定有一个为 \(n\) 号节点
- 对于一个 \(n\) 度点，其会在 prufer 序列中出现 \(n-1\) 次
应用：
无向完全图生成树计数：若该完全图点数为 \(n\)，则任意一个长度为 \(n-2\) 的值域为 \([1,n]\) 的序列都可以还原出一棵生成树，所以方案数即 \(n^{n-2}\)，与 Cayley 定理的结论一致。
Cayley 定理：假设图中有 \(m\) 个连通块，连通块内的点数为 \(a_1,a_2,\cdots,a_m\)，且满足 \(a_1 + a_2 + \cdots + a_m = n\)，则选择 \(m-1\) 条边将图联通的方案数为 \(n^{m-2}\prod_{i=1}^m a_i\)
广义 Cayley 定理：\(n\) 个有标号的点形成的包含 \(k\) 棵无向树的森林，要求给定的 \(k\) 个点没有两个点属于同一棵树的方案数为 \(k \times n^{n-k-1}\)。
\(n\) 个点的有根树计数：因为每个点都可以作为根，所以答案为 \(n \times n^{n-2} = n^{n-1}\)
容斥原理
最基本的式子就是交集与并集的转化：
设 \(S\) 为有限集，\(A_i \subseteq S（i \in [1,n]）\)，则有：
证明：考虑元素 \(x\) 属于 \(m\) 个 \(A\)，则其产生的贡献就是这个式子 \(\sum_{i=1}^m (-1)^{i-1} \binom{m}{i} = -(\sum_{i=1}^m (-1)^i \binom{m}{i}) = -(-1 + \sum_{i=0}^m (-1)^i \binom{m}{i}) = -(-1 + (1-1)^m) = 1\)
直观理解这个式子就是将满足 \(A_1\) 或满足 \(A_2\) 或 \(\cdots\) 的元素个数转化为了强制同时满足某些条件的元素个数。
当然有的时候也要有一些直观的理解，比如 \([a,b]\) 中满足 \(A\) 的数的个数可以转化为 \([1,b]\) 中满足的个数减去 \([1,a-1]\) 中满足的个数；满足 \(A\) 的个数可以转化为无所谓的个数减去不满足 \(A\) 的个数等。
在容斥以及反演过程中常使用二项式定理证明结论。
反演
反演其实就是容斥原理的代数形式，下面就简单介绍几种反演。
通过这些反演推导的练习，相信你一定会学会如何推导容斥系数。
二项式反演
形式一：
证明：
这里只证明充分性，必要性显然成立。
也就是得到在计算 \(G(n)\) 的时候 \(G(i)\) 的系数是多少，要证明的就是后面这个式子 \(G(n)\) 的系数为 \(1\)，其余的系数为 \(0\)。
下面就是考虑计算 \(G(i)\) 的系数，一个想法就是枚举所有的 \(F(j)\) 然后将 \(F(j)\) 中 \(G(i)\) 的系数求和。
所以系数就正确了，得证。
形式二：
证明：
考虑使用 EGF 证明；
这个式子显然就是一个卷积的形式也就是：
所以：
移项之后就是：
得证。
形式三：
形式四：
这两种形式都可以通过慢慢推的方式证明，因为形式一已经类似证明过了就不证明了。
莫比乌斯反演
请查看：
Min-Max 容斥
定义全集 \(U = \{a_1,a_2,a_3,\cdots,a_n\}\)，有一个集合 \(S\)，则 \(\max(S) = \max \limits_{a_i \in S} a_i\)，\(\min(S) = \min \limits_{a_i\in S} a_i\)。
则有如下结论：
下面考虑证明第一个式子。
一样的套路，假设元素 \(x\) 为第 \(k\) 大，钦定 \(x\) 为集合中的最小值，那么它在后面的式子里对答案贡献的系数是什么，可以枚举大于 \(x\) 的数选择多少个。
所以只有最大值会产生 \(1\) 的贡献，其他都会产生 \(0\) 的贡献，得证。
要注意的一点就是 Min-Max 容斥在期望意义下依然成立，即：
如果我们要求第 \(k\) 大也是可以容斥出来的：
这个容斥系数我们是可以很简单推导出来的。
考虑设：
考虑若 \(x\) 为第 \(p\) 大，则由上文可知其贡献即：
我们的目的就要让这个式子的值等于 \([p=k]\)，也就是：
这个就是一个二项式反演的形式，所以就有：
因此 \(F(|T|) = (-1)^{|T|-k}\binom{|T|-1}{k-1}\)
子集反演
莫比乌斯反演相当于在因子多重集上的子集反演，所以本质也是子集反演。
现有一个满足某些条件的元素集合 \(A\)。
设 \(f(S)\) 表示 \(A=S\) 时的答案，\(g(S)\) 表示 \(S \subseteq A\) 时的答案，则有如下结论：
设 \(f(s)\) 表示满足 \(A=S\) 时的答案，\(g(S)\) 表示 \(A \subseteq S\) 时的答案，则有如下结论：
斯特林反演
定义第一类斯特林数 \(\begin{bmatrix}n \\ m\end{bmatrix}\) 表示 \(n\) 个不同元素形成 \(m\) 个圆排列的方案数。
注意 \((1,2,3,4)\) 与 \((2,3,4,1)\) 为同一个圆排列，但 \((1,2,3,4)\) 与 \((4,3,2,1)\) 不是同一个圆排列。
其满足如下递推式：
这个递推式就是考虑元素 \(n\) 是自己单独变成一个圆排列还是放到前 \(n-1\) 个数的前面。
对于任意一个排列我们如果将其变成置换的形式，就相当于划分成了若干圆排列，也就是说：
定义第二类斯特林数 \(\begin{Bmatrix} n \\ m\end{Bmatrix}\) 表示将 \(n\) 个不同的元素划分到 \(m\) 个相同的集合中，要求集合非空的方案数。
则有如下的递推式：
就是考虑元素 \(n\) 是自己新建一个集合，还是放在前面已有的集合中。
可以显然发现这个结论：
因为一个圆排列只对应一个集合，而一个集合可以对应多个圆排列。
斯特林数最关键的应用就是：普通幂、上升幂、下降幂之间的转换。
定义下降幂：\(x^{\underline{n}} = x\times (x-1) \times (x-2) \times \cdots \times (x-n+1)\)。
定义上升幂：\(x^{\overline{n}} = x \times (x+1) \times (x+2) \times \cdots \times (x+n-1)\)。
显然若 \(x < n\)，则 \(x^{\underline{n}} = 0\)。
普通幂转下降幂：
证明：
考虑使用数学归纳法，显然 \(n=0\) 时成立，考虑假设 \([0,n-1]\) 成立，证明 \(n\) 时成立。
上升幂转通常幂：
证明同上。
下降幂转通常幂：
通常幂转上升幂：
上述两个式子的证明：
首先这个式子成立：
将这个式子分别带入第一、二个公式即可得到这两个式子。
反转公式：
证明：
将第三、四个公式，分别带入第一、二个公式就可以得到这个公式。
斯特林反演：
下面只证明一下第一个式子的充分性，其余的都可以类比地推出。
线性代数
矩阵乘法
若给定矩阵 \(A,B\)，使得 \(C = A \times B\)，则满足：\(c_{i,j} = \sum_{k} (A_{i,k} \times B_{k,j})\)
也就是说若 \(A,B\) 可以进行矩阵乘法则必须要满足：\(A\) 的列数等于 \(B\) 的行数。
矩阵乘法之后的 \(C\) 矩阵 \((i,j)\) 位置的元素，相当于 \(A\) 的第 \(i\) 行与 \(B\) 的第 \(j\) 列对应相乘再相加后的结果。
矩阵乘法之后的 \(C\) 矩阵的行数等于 \(A\) 的行数，列数等于 \(B\) 的列数。
矩阵乘法满足结合律，但不满足交换律，即若我们要计算 \(A^k\) 也可以用类似快速幂的方法进行计算。
我们可以将矩阵乘法中的运算更换，比如换成：\(c_{i,j} = \max_{k} (A_{i,k} + B_{k,j})\)，这个东西叫做 \(\max+\)矩乘，可以证明这种形式的矩阵乘法也满足结合律。
而我们的许多 \(dp\) 中的转移方程就可以用这种矩阵表示出来，所以就可以通过矩阵乘法在 \(O(\log n)\) 的时间内进行 \(dp\) 或者快速维护动态 \(dp\)。
高斯消元
请查看：
本文只会扩展一下高斯消元的应用，主要是这种加减消元法的思想。
解异或方程组
记 \(\oplus\) 为按位 xor 操作，解下列方程组：
其中 \(a_{i,j} \in \{0,1\}\)
注意到一点 \(a \oplus a = 0\)，也就是我们可以使用这点性质进行消元。
过程与高斯消元相同，因为我们每次只需要支持行的交换和行的对应异或所以可以使用 bitset 优化到 \(O(\frac{n^3}{w})\)。
矩阵求逆
对于方阵 \(A\) 若方阵 \(A^{-1}\) 满足 \(A \times A^{-1} = A^{-1} \times A = I\)，则称矩阵 \(A\) 可逆，其中 \(A^{-1}\) 就是它的逆矩阵。
记 \(I_n\) 表示 \(n\times n\) 的单位矩阵，则逆矩阵的求法如下：
- 构造一个 \(n \times 2n\) 的矩阵 \((A,I_n)\)。
- 通过高斯消元将矩阵变成 \((I_n,A^{-1})\)，这样右半部分的矩阵就是 \(A\) 的逆矩阵 \(A^{-1}\)，若左边不可以化为 \(I_n\) 则矩阵 \(A\) 不可逆。
行列式求值
对于一个 \(n \times n\) 的行列式 \(A\)，其行列式的值定义为：
其中 \(S_n\) 定义为长度为 \(n\) 的全排列集合，\(\text{sgn}(\sigma)\) 定义为排列 \(\sigma\) 的奇偶性，若 \(\sigma\) 中逆序对数为偶数则 \(\text{sgn}(\sigma) = 1\)，否则 \(\text{sgn}(\sigma) = -1\)
行列式有如下性质：
-
交换两行（列）行列式的值取反
证明：若交换 \(x,y\) 两行，则考虑贡献是怎么变化的，如果要使得 \(\prod_{i=1}^n a_{i,\sigma_i}\) 依旧是之前的值，就相当于要交换 \(\sigma_x\) 和 \(\sigma_y\)，此时 \(\sigma_x,\sigma_y\) 是否构成逆序对的情况取反，而对于 \(p\in(x,y)\)，\(\sigma_p\) 是否与 \(\sigma_x,\sigma_y\) 构成逆序对的情况要么同时改变，要么同时不变，所以不会有影响，对于 \(p\in [1,x) \bigcup (y,n]\)，\(\sigma_p\) 是否与 \(\sigma_x,\sigma_y\) 构成逆序对显然不会有任何影响。
综上逆序对恰好变化 \(1\)，也就是奇偶性会改变，会乘以 \(-1\)。 -
将一行（列）加到另一行（列）上行列式的值不变
证明：若将 \(x\) 列加入到 \(y\) 列上，那么对于一个排列 \(\sigma\) 交换 \(\sigma_x\) 与 \(\sigma_y\) 后可以得到一个新的排列 \(\sigma'\)，显然 \(\text{sgn}(\sigma) = -\text{sgn}(\sigma')\)，而对于多加的贡献在两者中正好形成相反数所以相互抵消了。 -
若行列式只有 \(a_{i,j}(i \le j)\) 处有值，即一个上三角处有值，则该行列式的值为 \(\prod_{i=1}^n a_{i,i}\)
证明：此时对于一个排列 \(\sigma\) 要使得 \(\prod_{i=1}^n a_{i,\sigma_i}\) 不为 \(0\)，只有 \(\sigma = \{1,2,3,4,\cdots,n\}\)，而此时 \(\text{sgn}(\sigma) = 1\)，所以行列式的值就是 \(\prod_{i=1}^n a_{i,i}\) -
将行列式某行（列）同时乘 \(k\)，则行列式的值乘 \(k\)
证明：相当于对于每个 \(\sigma\) 都将某个 \(a_{i,\sigma_i}\) 乘以 \(k\)，所以最后的值就会乘以 \(k\)。
通过上述性质我们就可以直接通过高斯消元将行列式消成上三角，然后对角线元素的乘积就是行列式的值。
需要注意如果消的过程中交换了一次行，要将最后的答案乘以 \(-1\)。
LGV 引理
LGV 引理常用于解决 DAG 上不相交路径（权值）计数问题
记 \(w(P)\) 表示 \(P\) 这条路径的权值和，若为路径计数则可将权值记为 \(1\)。
记 \(e(u,v)\) 表示 \(u\) 到 \(v\) 所有路径 \(P\) 的 \(w(P)\) 之和。
记起点集合为 \(A\)，终点集合大小为 \(B\)，其大小均为 \(n\)。
则我们的答案为下列行列式的值：
感觉这个如果不给例题就实在是太抽象了。
例题 CF348D Turtles：
一张 \(n\) 行 \(m\) 列的网格图，图中的有些格子上面有障碍物，但保证 \((1,1)\) 和 \((n,m)\) 上面都没有障碍物。在 \((1,1)\) 处有两只乌龟，都想要去 \((n,m)\)。乌龟每次都可以向下或者向右走一格，前提是格子上没有任何障碍物。要求两只乌龟在前往 \((n,m)\) 的路途中不可以相遇，即除了起点和终点，他们的路径没有其他公共点。求出从起点到终点的不同路径对数。答案对 \(10^9+7\) 取模。
考虑我们从 \((1,1)\) 出发必然经过 \((1,2)\) 和 \((2,1)\) 到达 \((n,m)\) 必然经过 \((n-1,m)\) 和 \((n,m-1)\)，所以我们的起点集合就是 \(A = \{(1,2),(2,1)\}\) 终点集合就是 \(B = \{(n-1,m),(n,m-1)\}\)。
根据 LGV 引理，我们要算四次 \(e(i,j)\) 表示从 \(i\) 到 \(j\) 的路径条数，而这个东西 \(O(nm)\) 的 \(dp\) 做法显然，就很好做了。
矩阵树定理
矩阵树定理可以解决给定一张图，求其生成树个数，这里要求给定的图没有自环。
下面考虑无向图的情况。
给定一张图 \(G = (V,E)\)，\(m_{i,j}\) 表示直接连接 \((i,j)\) 的边数，\(deg_i\) 表示点 \(i\) 的度数，定义它的拉普拉斯矩阵 \(L\) 为：
则生成树个数为 \(L\) 中任意删去一行一列后其行列式的值。
下面考虑有向图的情况。
记 \(m_{i,j}\) 表示从 \(i\) 指向 \(j\) 的边数，定义出度拉普拉斯矩阵为：
定义入度拉普拉斯矩阵为：
记图 \(G\) 的以 \(r\) 为根的根向生成树的方案数为 \(t^{root}(G,r)\)，记图 \(G\) 的以 \(r\) 为根的叶向生成树的方案数为 \(t^{leaf}(G,r)\)，则根据矩阵树定理有：
其中定义 \(L\binom{1,2,3,\cdots,k-1,k+1,\cdots,n}{1,2,3,\cdots,k-1,k+1,\cdots n}\) 表示 \(L\) 矩阵除去第 \(k\) 行第 \(k\) 列后的矩阵。
BEST 定理
定义 \(t^{root}(G,k)\) 表示图 \(G\) 的以 \(k\) 为根的根向生成树个数。
在有向欧拉图 \(G\) 中，\(G\) 中不同欧拉回路的数量为：
\(deg_v\) 既可以指出度也可以指入度，因为欧拉图中每个点的入度和出度相等。
\(k\) 可以为任意点，因为此时对于任意两个点 \(u,v\) 都有 \(t^{root}(G,x) = t^{root}(G,y)\)。
一种感性理解这个定理的方法：
对于一条欧拉路径，我们保留每一个点的最后一条出边，出边一定构成一棵根向树，因为如果不是就无法构成欧拉路径。
而对于其它的边发现任意排列都可以构成欧拉路径，所以就是\(\prod_{v \in V} (deg_v-1)!\)。
乘起来就是 BEST 定理。
多项式与生成函数
请查看：
群论入门
请查看：
计算几何
请查看：
博弈论
请查看：
