【题解】DP选练(23.9.11 - 23.9.12)
一些写过题解的题我就直接挂连接了。
[NOIP2018 提高组] 货币系统
题目描述:
在网友的国度中共有 种不同面额的货币,第 种货币的面额为 ,你可以假设每一种货币都有无穷多张。为了方便,我们把货币种数为 、面额数组为 的货币系统记作 。
在一个完善的货币系统中,每一个非负整数的金额 都应该可以被表示出,即对每一个非负整数 ,都存在 个非负整数 满足 的和为 。然而, 在网友的国度中,货币系统可能是不完善的,即可能存在金额 不能被该货币系统表示出。例如在货币系统 , 中,金额 就无法被表示出来。
两个货币系统 和 是等价的,当且仅当对于任意非负整数 ,它要么均可以被两个货币系统表出,要么不能被其中任何一个表出。
现在网友们打算简化一下货币系统。他们希望找到一个货币系统 ,满足 与原来的货币系统 等价,且 尽可能的小。他们希望你来协助完成这个艰巨的任务:找到最小的 。
【数据范围】
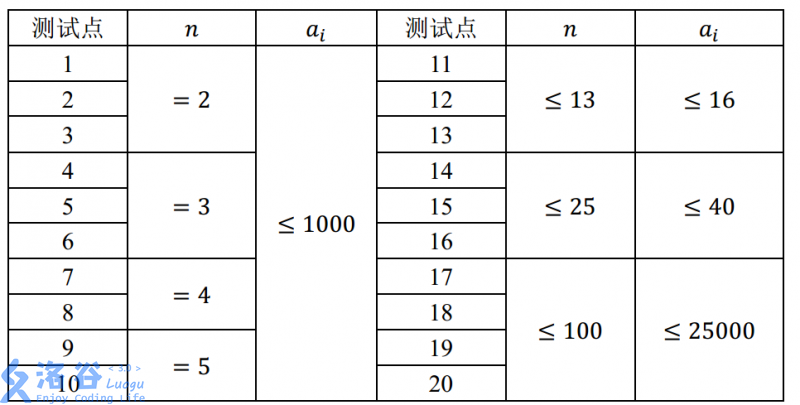
对于 的数据,满足 。
题目分析:
一个结论: 必然为 除去其中的部分元素得到。
考虑如果 中拥有 没有的元素,如果这个元素可以被表示出来那么多出这个元素是没有意义的,如果这个元素不可以被表示出来那么这个元素会多表示出一些数。
所以我们只需要判断 中哪些元素会被内部的元素表示出,然后将这些元素删除即可,这个直接做一次背包就可以求得。
[CSP-S2020] 函数调用
题目描述:
函数是各种编程语言中一项重要的概念,借助函数,我们总可以将复杂的任务分解成一个个相对简单的子任务,直到细化为十分简单的基础操作,从而使代码的组织更加严密、更加有条理。然而,过多的函数调用也会导致额外的开销,影响程序的运行效率。
某数据库应用程序提供了若干函数用以维护数据。已知这些函数的功能可分为三类:
- 将数据中的指定元素加上一个值;
- 将数据中的每一个元素乘以一个相同值;
- 依次执行若干次函数调用,保证不会出现递归(即不会直接或间接地调用本身)。
在使用该数据库应用时,用户可一次性输入要调用的函数序列(一个函数可能被调用多次),在依次执行完序列中的函数后,系统中的数据被加以更新。某一天,小 A 在应用该数据库程序处理数据时遇到了困难:由于频繁而低效的函数调用,系统在执行操作时进入了无响应的状态,他只好强制结束了数据库程序。为了计算出正确数据,小 A 查阅了软件的文档,了解到每个函数的具体功能信息,现在他想请你根据这些信息帮他计算出更新后的数据应该是多少。
【数据范围】
| 测试点编号 | 其他特殊限制 | ||
|---|---|---|---|
| 无 |
对于所有数据:,,,,,。
题目分析:
一个想法就是倒序操作,因为注意到如果有以下四个操作:
那么 贡献了 次, 贡献了 次,也就是加法操作的贡献次数等于其后面执行的乘法的乘积。
这样直接建图跑拓扑序,再拼点部分分就有了 分。
这种类型的题如果想要快速维护,一个显然的想法就是求出每一个操作的操作次数,这样就直接跑一遍拓扑序就可以得到答案。
但是这样显然不行,因为乘法操作会对加法操作产生影响,但是我们可以将这个影响化为等次数的操作,也就是后面的 操作,我们将其看作这个加法操作需要执行 次。
这样我们就可以得到加法的等效操作次数,这样直接跑一遍拓扑序然后将这个等效次数每次向下传递就好了。
现在的一个问题就是我们需要知道到底乘了多少,才能得到等效操作次数,这个东西可以直接维护 表示跑完了 点开始的拓扑序之后,对乘法造成的贡献为 ,建反图跑拓扑序这个东西就可以被维护出来。
注意我们要求倒叙操作。
[APIO2010] 特别行动队
题目描述:
你有一支由 名预备役士兵组成的部队,士兵从 到 编号,你要将他们拆分成若干特别行动队调入战场。出于默契的考虑,同一支特别行动队中队员的编号应该连续,即为形如 的序列。所有的队员都应该属于且仅属于一支特别行动队。
编号为 的士兵的初始战斗力为 ,一支特别行动队的初始战斗力 为队内士兵初始战斗力之和,即 。
通过长期的观察,你总结出对于一支初始战斗力为 的特别行动队,其修正战斗力 ,其中 是已知的系数()。 作为部队统帅,现在你要为这支部队进行编队,使得所有特别行动队的修正战斗力之和最大。试求出这个最大和。
对于 的数据,,,,,。
题目分析:
这个题显然需要用 来做,可以设 表示考虑了前 个士兵战斗力之和的最大值,转移就是枚举最后一段是什么,为了方便记 :
这个东西就给人一种可以斜率优化的感觉,所以拆拆式子看看是不是可以:
这个东西就可以化简为 的形式,其中:
所以如果我们将所有的 拿出来放到二维平面上,这个东西就相当于拿一条斜率为 的直线去切这些点,使得其 轴的截距最大。
使得截距最大的点一定是在上凸包上,所以可以直接维护上凸包,而我们在枚举的过程中斜率一定单调递增,所以可以直接单调队列维护一下凸包就可以了。
[NOI2015] 寿司晚宴
题目描述:
为了庆祝 NOI 的成功开幕,主办方为大家准备了一场寿司晚宴。小 G 和小 W 作为参加 NOI 的选手,也被邀请参加了寿司晚宴。
在晚宴上,主办方为大家提供了 种不同的寿司,编号 ,其中第 种寿司的美味度为 。(即寿司的美味度为从 到 )
现在小 G 和小 W 希望每人选一些寿司种类来品尝,他们规定一种品尝方案为不和谐的当且仅当:小 G 品尝的寿司种类中存在一种美味度为 的寿司,小 W 品尝的寿司中存在一种美味度为 的寿司,而 与 不互质。
现在小 G 和小 W 希望统计一共有多少种和谐的品尝寿司的方案(对给定的正整数 取模)。注意一个人可以不吃任何寿司。
题目分析:
互质就是 ,这个东西放到质因数分解的形势下就是没有公共的质因数。
这样的话当 比较小的时候就直接记录两个人分别选了哪些质因数就好了。
当 比较大的时候直接记录就炸了,但是我们知道一个数大于 的质因子只会有最多一个,所以可以按照这个质因子分类讨论。
也就是将大于 的质因子相同的数看作一组,这样一组只能被第一个人选择或者只能被第二个人选择,可以分别做 记录小于 的质因子的选择情况,然后最后合并在一起就好了。
较小的质因子我们只需要取到前 个质数,所以时间复杂度为
[NOIP2018 普及组] 摆渡车
题目描述:
有 名同学要乘坐摆渡车从人大附中前往人民大学,第 位同学在第 分钟去 等车。只有一辆摆渡车在工作,但摆渡车容量可以视为无限大。摆渡车从人大附中出发、 把车上的同学送到人民大学、再回到人大附中(去接其他同学),这样往返一趟总共花费 分钟(同学上下车时间忽略不计)。摆渡车要将所有同学都送到人民大学。
凯凯很好奇,如果他能任意安排摆渡车出发的时间,那么这些同学的等车时间之和最小为多少呢?
注意:摆渡车回到人大附中后可以即刻出发。
。
题目分析:
首先一个显然的结论就是,一个人一定是选择到达时间最近的摆渡车被送走,所以考虑如果我们已经知道了摆渡车出发的时间 ,要求 ,那么最小的等车时间是多少。
考虑如果 ,那么 的等车时间就是 ,所以总的等车时间就是很好算的就是将贡献拆开统计,设 表示到达时间在 的同学个数,则:
需要注意的一点是这里默认 。
因为后面的 之和固定,所以最优化答案的时候不用管,只需要管前面的部分,而前面的部分显然就是枚举摆渡车在什么时候出发,也就是设 表示摆渡车最后一次出发时候为 的最小等车时间,转移就是枚举上一次出发的时间:
这东西可以拆成斜率优化的形式,也就是:
可以令 ,,,
所以直接维护凸包然后就好了,因为斜率递增可以单调队列维护。
[NOI2009] 诗人小G
题目描述:
小 G 是一个出色的诗人,经常作诗自娱自乐。但是,他一直被一件事情所困扰,那就是诗的排版问题。
一首诗包含了若干个句子,对于一些连续的短句,可以将它们用空格隔开并放在一行中,注意一行中可以放的句子数目是没有限制的。小 G 给每首诗定义了一个行标准长度(行的长度为一行中符号的总个数),他希望排版后每行的长度都和行标准长度相差不远。显然排版时,不应改变原有的句子顺序,并且小 G 不允许把一个句子分在两行或者更多的行内。在满足上面两个条件的情况下,小 G 对于排版中的每行定义了一个不协调度, 为这行的实际长度与行标准长度差值绝对值的 次方,而一个排版的不协调度为所有行不协调度的总和。
小 G 最近又作了几首诗,现在请你对这首诗进行排版,使得排版后的诗尽量协调(即不协调度尽量小),并把排版的结果告诉他。
数据规模与约定
| 测试点 | ||||
|---|---|---|---|---|
所有句子的长度不超过 。
题目分析:
一个显然的想法就是 解决这个问题,我们 所做的决策显然是每一行放哪些句子,也就是可以显然想到设 表示考虑了前 个句子最小的不协调度之和。
转移就是枚举最后这一行放了哪些句子,设 表示前 个句子的和:
转移需要注意的一点就是有空格,需要减去空格。
通过一些显然的观察或者是打表可以发现这个 满足决策单调性,所以直接上套路做法就可以了。
[Cnoi2020] 线形生物
题目描述:
线形生物要从 号台阶走到 号台阶。
最开始, 号台阶都有一条连向下一台阶的有向边 。
之后 Cirno 加入了 条返祖边 ,它们构成了一个返祖图。
线形生物每步会 等概率地 选取当前台阶的一条出边并走向对应的台阶。
当走到 号台阶时,线形生物就会停止行走。
同时,Cirno 会统计线性生物总共走的步数,记作 。
Cirno 想知道 (即 的数学期望)对 取模后的结果。
对于 的数据,保证:,,。
题目分析:
显然需要使用 解决这个问题,这种问题的一种经典 设法就是设 表示从 号台阶到 号台阶的期望步数,为了方便设 ,给定的 条边构成边集 ,则转移就是:
转移就是枚举下一步走的是什么,这样的转移就会造成自环的情况,所以考虑把这种情况移项直接搞掉:
因为我们转移是从小到大枚举 ,所以每次只需要维护以 为右端点的 的值,可以使用树状数组增量维护。
最后我们的答案显然就是
[NOI2019] 回家路线
题目描述:
猫国的铁路系统中有 个站点,从 编号。小猫准备从 号站点出发,乘坐列车回到猫窝所在的 号站点。它查询了能够乘坐的列车,这些列车共 班,从编号。小猫将在 时刻到达 号站点。对于 号列车,它将在时刻 从站点 出发,在时刻 直达站点 ,小猫只能在时刻 上 号列车,也只能在时刻 下 号列车。小猫可以通过多次换乘到达 号站点。一次换乘是指对于两班列车,假设分别为 号与 号列车,若 并且 ,那么小猫可以乘坐完 号列车后在 号站点等待 个时刻,并在时刻 乘坐 号列车。
小猫只想回到猫窝并且减少途中的麻烦,对此它用烦躁值来衡量。
-
小猫在站点等待时将增加烦躁值,对于一次 个时刻的等待,烦躁值将增加 ,其中 是给定的常数。注意:小猫登上第一班列车前,即从 时刻起停留在 号站点的那些时刻也算作一次等待。
-
若小猫最终在时刻 到达 号站点,则烦躁值将再增加 。
形式化地说,若小猫共乘坐了 班列车,依次乘坐的列车编号可用序列 表示。该方案被称作一条可行的回家路线,当且仅当它满足下列两个条件:
-
,
-
对于所有 ,满足 且
对于该回家路线,小猫得到的烦躁值将为:
小猫想让自己的烦躁值尽量小,请你帮它求出所有可行的回家路线中,能得到的最
小的烦躁值。题目保证至少存在一条可行的回家路线。
对于所有测试点:。
题目分析:
至少感觉写出来 之后就十分类似 [APIO2010] 特别行动队了。
显然我们可以考虑设 表示现在在 号车站,时间为 的最少烦恼值,转移就是枚举是由之前的车站移动过来还是由之前的车站转移过来。
只有 种有用的状态,以及第一种转移最多 次,所以可以把重心放在第二种转移上,也就是下面这种形式:
这个东西就是一个斜率优化的形式,我就不推了。
但是注意到我们的转移顺序特别离谱,如果枚举 进行转移就会出大问题,所以考虑对时间从小到大扫描线,然后每一次将第二维为枚举时间的状态更新,这样顺序就合法了。
以及如果我们直接从 因为可能 这个状态本身就是等待一段时间得来的,所以要分别记录等待了一段时间的 值和没有等待时间也就是只由第一种转移得来的 值。
还有一点细节就是即使我们没有等待任何时间,对烦恼值也有 的贡献。
斜率优化就是对于每一个 都维护一个凸包就好了,代码不是很难写。
[ZJOI2008] 骑士
题目描述:
Z 国的骑士团是一个很有势力的组织,帮会中汇聚了来自各地的精英。他们劫富济贫,惩恶扬善,受到社会各界的赞扬。
最近发生了一件可怕的事情,邪恶的 Y 国发动了一场针对 Z 国的侵略战争。战火绵延五百里,在和平环境中安逸了数百年的 Z 国又怎能抵挡的住 Y 国的军队。于是人们把所有的希望都寄托在了骑士团的身上,就像期待有一个真龙天子的降生,带领正义打败邪恶。
骑士团是肯定具有打败邪恶势力的能力的,但是骑士们互相之间往往有一些矛盾。每个骑士都有且仅有一个自己最厌恶的骑士(当然不是他自己),他是绝对不会与自己最厌恶的人一同出征的。
战火绵延,人民生灵涂炭,组织起一个骑士军团加入战斗刻不容缓!国王交给了你一个艰巨的任务,从所有的骑士中选出一个骑士军团,使得军团内没有矛盾的两人(不存在一个骑士与他最痛恨的人一同被选入骑士军团的情况),并且,使得这支骑士军团最具有战斗力。
为了描述战斗力,我们将骑士按照 至 编号,给每名骑士一个战斗力的估计,一个军团的战斗力为所有骑士的战斗力总和。
对于 的测试数据,满足 ,每名骑士的战斗力都是不大于 的正整数。
题目分析:
我们其实就是要解决最大权独立集问题,一般图的话根本不能做。
但是注意我们这一张图是一个基环树,也就是我们可以使用处理环的一般方法断环为链,这样就变成了一棵树的问题,就可以随便做了。
断环为链其实就是直接钦定环上相邻的某两个点不能同时被选。
因为对于每一个环我们选择一对点即可,所以总时间复杂度 。
[NOIP2009 提高组] 最优贸易
题目描述:
国有 个大城市和 条道路,每条道路连接这 个城市中的某两个城市。任意两个城市之间最多只有一条道路直接相连。这 条道路中有一部分为单向通行的道路,一部分为双向通行的道路,双向通行的道路在统计条数时也计为 条。
国幅员辽阔,各地的资源分布情况各不相同,这就导致了同一种商品在不同城市的价格不一定相同。但是,同一种商品在同一个城市的买入价和卖出价始终是相同的。
商人阿龙来到 国旅游。当他得知同一种商品在不同城市的价格可能会不同这一信息之后,便决定在旅游的同时,利用商品在不同城市中的差价赚回一点旅费。设 国 个城市的标号从 ,阿龙决定从 号城市出发,并最终在 号城市结束自己的旅行。在旅游的过程中,任何城市可以重复经过多次,但不要求经过所有 个城市。阿龙通过这样的贸易方式赚取旅费:他会选择一个经过的城市买入他最喜欢的商品――水晶球,并在之后经过的另一个城市卖出这个水晶球,用赚取的差价当做旅费。由于阿龙主要是来 国旅游,他决定这个贸易只进行最多一次,当然,在赚不到差价的情况下他就无需进行贸易。
假设 国有 个大城市,城市的编号和道路连接情况如下图,单向箭头表示这条道路为单向通行,双向箭头表示这条道路为双向通行。
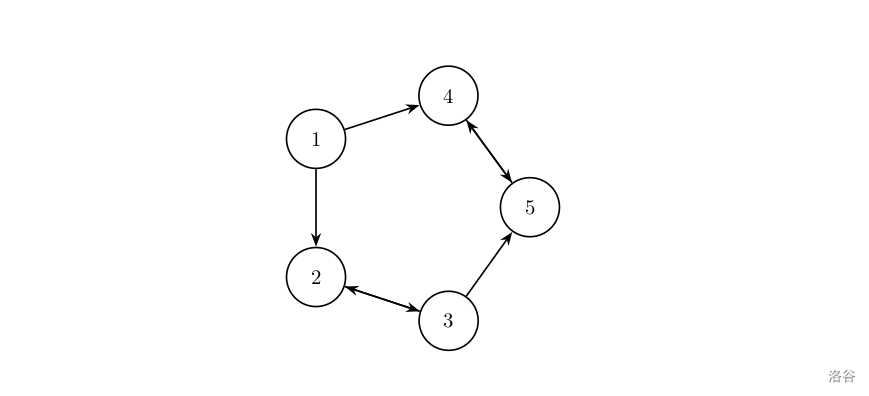
假设 号城市的水晶球价格分别为 。
阿龙可以选择如下一条线路:,并在 号城市以 的价格买入水晶球,在 号城市以 的价格卖出水晶球,赚取的旅费数为 。
阿龙也可以选择如下一条线路:,并在第 次到达 号城市时以 的价格买入水晶球,在第 次到达 号城市时以 的价格卖出水晶球,赚取的旅费数为 。
现在给出 个城市的水晶球价格, 条道路的信息(每条道路所连接的两个城市的编号以及该条道路的通行情况)。请你告诉阿龙,他最多能赚取多少旅费。
对于 的数据,,,,, 各城市的编号 。
水晶球价格 。
题目分析:
一个显然的想法就是对图缩点,这样被缩到一起的点就可以相互到达,缩完点后的图就是一个 DAG。
要使得价值最大,我们显然就是要低买高卖,也就是可以考虑设 表示从 到 的路径中最低的水晶球价格是多少,然后考虑在 点卖掉,可以设 表示从 到 进行一次交易的最优贡献,然后每次更新 并向下传递即可。
最后的答案就是 。
一些写过题解的题
可能以后会把题解直接搬过来吧,或者自己再写一份。
P6748 『MdOI R3』Fallen Lord
[CSP-S2019] Emiya 家今天的饭
[九省联考 2018] 一双木棋 chess
[八省联考 2018] 林克卡特树
不同子串个数
[六省联考 2017] 分手是祝愿




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律