【题解】AtCoder Regular Contest 163 A-D
E 太过于 adhoc，F 太过于神仙，就不做了。
A.Divide String
题目描述：
多组数据。
给出一个长为 \(N\) 的字符串，问能否将其划分为多段，使字典序严格上升，保证 \(\sum{N}\le2000\)。
$ 2\ \le\ N\ \le\ 2000 $
题目分析：
考虑如果划分为三段，使得其满足 \(S_1 < S_2 < S_3\)，则必然满足 \(S_1 < S_2 + S_3\)
所以我们完全没必要划分为三段及以上，划分为两段就足够了。
可以直接枚举划分的分界点，然后 \(O(n)\) 判断是否合法。
代码：
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N = 2005;
char s[N];
bool chk(int l,int mid,int r){
int len1 = mid - l + 1;
int len2 = r - (mid+1) + 1;
int posl = l,posr = mid+1;
while(posl <= mid && posr <= r && s[posl] == s[posr]){
++posl,++posr;
}
if(posl > mid || posr > r) return len1 < len2;
return s[posl] < s[posr];
}
int main(){
int T;scanf("%d",&T);
while(T--){
int n;scanf("%d",&n);
scanf("%s",s+1);
bool flag = false;
for(int i=1; i<n; i++){
if(chk(1,i,n)){
flag = true;
break;
}
}
if(flag) printf("Yes\n");
else printf("No\n");
}
return 0;
}
B.Favorite Game
题目描述：
给定 \(N,M\) 和数列 \({A_N}\)。定义一次操作为任取一个 \(A_i(1\le i\le N)\) 加一或减一。求经过几次操作后可以使得至少有 \(M\) 个 \(i(3\le i\le N)\) 满足 \(A_1\le A_i \le A_2\)。
$ 3\ \le\ N\ \le\ 2\ \times\ 10^5 ， 1\ \le\ M\ \le\ N-2 ， 1\ \le\ A_i\ \le\ 10^9 $
题目分析：
首先我们一定是只会操作 \(a_1,a_2\)，因为操作 \(a_1,a_2\) 相当于对其余值整体的一个操作，这样做显然优于只操作一个。
最后满足条件的数一定在 \(a\) 排序后的数组上是一个连续的区间，所以可以直接枚举这个区间是什么，设左右端点分别为 \(a_l,a_r\)
则我们就是要通过操作让 \(a_1 \le a_l\) 且 \(a_2 \ge a_r\)，这个就可以随便做了。
代码：
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e6+5;
const int INF = 1e11+5;
vector<int> v1,v2;
int a[N],n,m;
signed main(){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
scanf("%lld%lld",&n,&m);
for(int i=1; i<=n; i++) scanf("%lld",&a[i]);
int tmp = INF;
int l = a[1],r = a[2];
sort(a+3,a+n+1);
for(int i=3; i + m - 1<=n; i++){
int res = 0;
if(l > a[i]) res += l - a[i];
if(r < a[i + m - 1]) res += a[i + m - 1] - r;
tmp = min(tmp,res);
}
printf("%lld\n",tmp);
return 0;
}
C.Harmonic Mean
题目描述：
给定正整数 \(N\)，你需要构造一个正整数序列 \(A_i\)，满足：
- \(\displaystyle\sum_{i=1}^n\frac{1}{A_i}=1\)
- \(A_i\) 互不相同；
- \(1\le A_i\le 10^9\)
多组数据，\(1\le T,N\le 500\)。
题目分析：
看到这个 \(\frac{1}{A_i}\) 一个能想到的东西就是 \(\frac{1}{k(k+1)} = \frac{1}{k} - \frac{1}{k+1}\)。
会发现这个相当于一个裂项的形式，也就是我们可以直接：
这个时候发现其实就基本能构造出来了，就是当 \(n = k \times (k+1)\) 的时候这种做法就寄了。
但是如果 \(n\) 满足这个形式，则 \(n-1\) 一定不满足这个形式，所以我们可以按 \(n-1\) 构造出一种方案，然后将所有数乘 \(2\) 后再加上数 \(2\) 就好了。
其实就是让 \(\sum_{i=1}^{n-1} \frac{1}{B_i} = \frac{1}{2}\) 然后再加 \(\frac{1}{2}\) 就好了。
代码：
点击查看代码
#include<bits/stdc++.h>
using namespace std;
vector<int> v;
void solve(int n){
for(int i=1; i<=n-1; i++) v.push_back(i * (i + 1));
v.push_back(n);
}
int main(){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
int T;scanf("%d",&T);
while(T--){
int n;scanf("%d",&n);
if(n == 2){
printf("No\n");
continue;
}
bool flag = false;
for(int i=1; i<=n; i++){
if(i * (i + 1) == n) flag = true;
}
if(flag){
solve(n-1);
for(int i=0; i<v.size(); i++) v[i] *= 2;
v.push_back(2);
}
else solve(n);
printf("Yes\n");
for(auto i : v) printf("%d ",i);
v.clear();
printf("\n");
}
return 0;
}
D.Sum of SCC
题目描述：
考虑一张竞赛图 \(G\)，其中有 \(N\) 个节点，节点编号为 \(1,2,\dots,N\)，且 \(G\) 满足：
- 对于 \(G\) 中的所有边 \(u\to v\)，恰好有 \(M\) 条边满足 \(u<v\)。
设 \(f(G)\) 表示图 \(G\) 中的强连通分量数量。请你求出所有满足条件的 \(G\) 的 \(f(G)\) 之和。
答案对 \(998244353\) 取模。
\(1\le N\le30\)，\(0\le M\le\frac{N(N-1)}2\)。
题目分析：
之前不大知道竞赛图的性质，下面稍微罗列一下：
性质一：竞赛图缩点之后成链状。
注意这里不是一条链而是链状，就如下图所示：
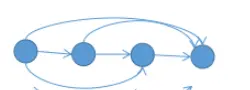
性质二：竞赛图的每一个强连通分量必然存在哈密顿回路
性质三：竞赛图必然存在哈密顿回路
因为缩点之后每一个点代表一个 SCC，所以可以推出下面这个结论：
一个竞赛图的 SCC 个数为将其点集划分为两个集合 \(A,B\)（可以为空）并满足以下限制的方案数减 \(1\)：
对于 \(u \in A，v \in B\) 的边 \((u,v)\)，其方向必然为 \(u \to v\)
有了这个结论也就是说我们可以直接对于每一个点 \(dp\) 求其属于 \(A\) 还是 \(B\)，就是直接求这个限制下划分的方案数。
因为题目里要求我们的统计的存在一个大小关系，所以不让从小到大插入点，也就是设 \(dp[i][j][k]\) 表示插入了编号为 \([1,i+j]\) 的点，\(|A| = i，|B| = j\)，满足题目条件的边数为 \(k\) 的方案数。
转移的话就是枚举 \(i+j+1\) 这个点插入到 \(A\) 还是 \(B\)，如下：
考虑放在 \(A\)，对于跨集合的边必然是 \(i+j+1 \to B\) 而因为 \(i + j + 1\) 必然是最大值也就是说这样的连边一定不满足条件，也就不用管；对于在集合内部的边就是枚举多少个满足条件即可。
考虑放在 \(B\)，对于跨集合的边必然是 \(A \to i+j+1\)，也就是一定满足条件，直接全加上就好；对于在集合内部的边就是枚举多少个满足条件即可。
也要注意最后把减 \(1\) 这个贡献也算上。
代码：
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 35;
const int MOD = 998244353;
int f[N][N][N*N],C[N*N][N*N];
signed main(){
int n,m;scanf("%lld%lld",&n,&m);
C[0][0] = 1;
for(int i=1; i<=n * n; i++){
C[i][0] = 1;
for(int j=1; j<=i; j++){
C[i][j] = (C[i-1][j] + C[i-1][j-1]) % MOD;
}
}
f[0][0][0] = 1;
for(int i=0; i<n; i++){
for(int j=0; i + j < n; j++){
for(int k=0; k<=m; k++){
for(int x=0; x<=i; x++)
if(k + x <= m) f[i+1][j][k+x] = (f[i+1][j][k+x] + f[i][j][k] * C[i][x])%MOD;
for(int x=0; x<=j; x++)
if(k + i + x <= m) f[i][j+1][k+i+x] = (f[i][j+1][k+i+x] + f[i][j][k] * C[j][x])%MOD;
}
}
}
int ans = 0;
for(int i=0; i<=n; i++) ans = (ans + f[i][n-i][m])%MOD;
ans = (ans - C[n * (n-1) / 2][m] + MOD)%MOD; //最后的 -1 产生的贡献
printf("%lld\n",ans);
return 0;
}
