【学习笔记】2023HDU多校(2)
别人打比赛都是学习人类智慧,而我打比赛却是在补基础知识[滑稽]
可能以后会补剩下的东西包括题解(
1.Alice Game
题目描述:
给定一个长度为 \(n\) 的序列和一个整数 \(k\),有两个人 Alice 和 Bob 可以进行以下两种操作之一:
1.选择一个长度小于等于 \(k\) 的连续段直接删除,若长度为 \(k\) 则必须满足其左右两边均为空
2.可以选择一个长度为 \(k\) 的连续段,满足这一段的左边和右边都不为空,然后将这一段删去,之后我们的删除连续段的操作不能跨越这一段
Alice 先手,求在两个人都绝顶聪明的情况下下谁获胜。
多测,\(T \le 10^4,k \le 10^7,n\le 10^9\)
题目描述:
这种题显然需要考虑打表 SG 函数吧。
考虑我们每次删除一个连续段,相当于创造出了两个相互独立的子游戏,所以这次操作的后继状态相当于这两个子游戏的 SG 的异或。
打完表其实序列大概是这个样子:
\(0[k\times 1]0[k\times 1][k\times 2]1[k\times 2][k\times 1]0\cdots\)
有循环节,所以直接找到 \(0\) 的通项公式,然后就可以直接判了。
代码:
打表代码:
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N = 2e5+5;
int SG[N],tag[N];
int main(){
// freopen("out.txt","w",stdout);
int n = 100,k = 10;
SG[0] = 0;
for(int i=1; i<=min(k,n); i++) SG[i] = 1;
for(int i=k+1; i<=n; i++){
for(int j=1; i-j-k>0; j++){
tag[SG[j] ^ SG[i - j - k]] = i;
}
while(tag[SG[i]] == i) ++SG[i];
}
for(int i=1; i<=n; i++) printf("%d",SG[i]);
return 0;
}
正经代码:
点击查看代码
#include<iostream>
using namespace std;
int main(){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
int T;scanf("%d",&T);
while(T--){
int k,n;scanf("%d%d",&k,&n);
bool flag = false;
if(n == 0) flag = true;
else if(n == k+1) flag = true;
else if(n > k + 1 && ((n - (k + 1)) % (4 * k + 2) == 0)) flag = true;
if(flag) printf("Bob\n");
else printf("Alice\n");
}
return 0;
}
2.Binary Number
题目描述:
给定长度为 \(n\) 的二进制数 \(s\),其中第一位为最高位,我们要进行恰好 \(k\) 次操作,每一次操作为选择 \([l,r]\) 将 \(s_l,s_{l+1},...,s_{r}\) 反转。
反转的意思为 \(1 \to 0\) 和 \(0 \to 1\)
询问能得到的最大的二进制数是多少
题目分析:
一个大细节题,感觉很震撼。
如果不考虑恰好 \(k\) 次的限制,我们肯定要从高到低每一次选择一段极长的 \(0\) 然后将它反转为 \(1\) 得到的就是最大值。
那么恰好 \(k\) 次该怎么做呢,我们下文均讨论 \(k\) 将 \(s\) 全部转化为 \(1\) 仍有多余的情况,因为如果都不够就不用管了。
我们可以通过操作同一个位置两次做到浪费掉 \(2\) 次操作,我们也可以通过操作 \([1,1][2,2][1,2]\) 浪费掉三次操作,那么通过 \(2,3\) 的自由组合我们就可以干掉除了 \(k=1\) 以外的所有情况,但是也要注意一点,我们消耗三次操作需要 \(n \ge 2\),所以要特判 \(n=1\) 的情况。
下面就是 \(k=1\) 有没有办法消耗掉。
首先就是我们每一次都操作一个极长的 \(0\) 的段,所以如果这一段长度大于等于 \(2\) 就可以分成两次来操作,就多消耗了一次操作。
或者如果我们 \(0\) 的旁边有 \(1\) 就可以先操作这个 \(1\) 然后将极长的 \(0\) 的段扩展 \(1\),也可以多消耗一次操作。
这样就可以通过这个题了,复杂度线性。
代码:
点击查看代码
#include<iostream>
#define int long long
using namespace std;
const int N = 2e5+5;
char s[N];
signed main(){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
int T;scanf("%lld",&T);int res = 0;
while(T--){
++res;
int n,k;scanf("%lld%lld",&n,&k);
scanf("%s",s+1);
if(n == 1){
if(k & 1) s[1] = (s[1] == '1' ? '0' : '1');
printf("%c",s[1]);
printf("\n");continue;
}
bool flag = false;
int flag2 = 0;
for(int i=1; i<=n; i++){
if(s[i] == '0'){
flag2 |= 1;
int ed = i;
for(;ed <= n && s[ed]=='0'; ++ed);
--ed;
if(k){
k--;
for(int j=i; j<=ed; j++) s[j] = '1';
if(ed - i + 1 >= 2) flag = true;
}
}
else if(s[i] == '1') flag2 |= 2;
}
if(k == 1 && !flag && flag2 != 3) s[n] = '0';
for(int i=1; i<=n; i++) printf("%c",s[i]);
printf("\n");
}
return 0;
}
3.Conuter Strike
题目描述:
给定一个 \(n\) 个点 \(m\) 条边的无向连通图,又给出了 \(k\) 个点记为 \(h_1,h_2,\ldots,h_k\),每次可以删除一个任意的点和 \(h\) 里面的前 \(q\) 个点,要求删除完成后必须满足这给定的 \(k\) 个点两两之间不连通,求 \(q\) 的最小值。
多测,\(T \le 5\times 10^3,2 \le n,m \le 2 \times 10^5,2 \le k \le n,\sum n,\sum m \le 10^6\)
题目分析:
这种给定一个序列,有限制的情况下选择前 \(q\) 个,要求最大/最小化 \(q\) 显然的思路就是二分答案,或者可以考虑增量法每次向里面加入一个点后判断。
感觉二分答案可能更好写一点,就考虑二分答案。
二分之后,问题就转化为了给定一张无向图,和一些询问点,要求是否存在一个点使得删去这个点之后所有的询问点互相不连通。
必经点,看上去就很圆方树,如果想节省一点复杂度可能可以再建虚树。
这样在树上 \(dfs\) 一遍就知道有多少条询问点之间的路径经过点 \(x\),那么只要存在一个圆点 \(x\) 使得所有的路径都会经过 \(x\) 那么删除这个点就是答案。
代码:
感觉有点难写,暂时咕咕咕
4.Card Game
题目描述:
给你 \(n\) 个柱子,初始时第 \(1\) 个柱子上有 \(k\) 个圆盘,且自底向上圆盘大小递减,每次可以将最上面一个圆盘移动到其他的柱子上,要求在任意时刻任意柱子的圆盘自底向上大小均依次递减,并且要将所有的圆盘都移动到第 \(2\) 个柱子上,询问给定 \(n\) 的情况下 \(k\) 的最大值是多少,答案对 \(998244353\) 取模。
多测 \(T \le 10^5,2 \le n \le 10^9\)
题目分析:
最后一步一定是将最大的移动到第 \(2\) 个柱子,然后将其他的圆盘按顺序移动回去,所以我们就考虑描述此时的局势,也就是一个空的终点牌堆和若干个有牌的牌堆。
所以不妨设 \(f[i]\) 表示有 \(i\) 个牌堆的最大数量,则显然 \(f[1] = 0,f[2] = 1\)。
考虑若 \(i > 2\),则我们依旧模拟这个过程,肯定是先移动最大的牌所在的堆这一步只有一个牌堆可以动,所以贡献为 \(f[1] + 1\),然后是次大的此时因为最大的牌堆可以随便用了,所以相当于 \(f[2] + 2\),即 \(f[i] = \sum_{j=1}^{n-1} (f[j] + 1)\),但是我们显然要化成通项公式。
将 \(f[i-1]\) 带入消一下得到:
放在二进制下理解的话可以显然得到 \(f[i] = 2^{i-1} - 1\)
代码:
点击查看代码
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int MOD = 998244353;
int mod(int x){
return x % MOD;
}
int power(int a,int b){
int res = 1;
while(b){
if(b & 1) res = mod(res * a);
a = mod(a * a);
b >>= 1;
}
return res;
}
signed main(){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
int T;scanf("%lld",&T);
while(T--){
int n;scanf("%lld",&n);
printf("%lld\n",(power(2,n-1) - 1 + MOD)%MOD);
}
return 0;
}
5.Or
题目描述:
给定两个长度为 \(n\) 的序列 \(a,b\),有 \(q\) 次询问,每次给出两个数 \(l,r\) 求:
其中 \(\oplus\) 代表二进制下的按位或操作。
题目分析:
各个位之间相互独立,所以考虑对于每一位单独计算贡献。
考虑若某一位为 \(1\) 则以后这一位将永远为 \(1\),也就是对于区间 \([l,r]\) 的询问第 \(k\) 位为 \(1\),则对于区间 \([l-a,r+b]\) 的询问第 \(k\) 位也为 \(1\)。
所以思路就很显然了,从左到右扫描线,对于每一个左端点处理出 \(R[l]\) 表示 \([l,R[l]]\) 为以 \(l\) 为左端点的极小的区间使得其第 \(k\) 位为 \(1\)。
那么只要对于左端点在 \(l\) 左边右端点在 \(R[l]\) 右边的询问区间第 \(k\) 位均为 \(1\),就非常好做了。
那么现在问题就在于处理 \(R[l]\),也就是怎么判断某两个位置之间的贡献的第 \(k\) 位为 \(1\),不妨设 \(pre[i] = \sum_{j=1}^i b[j]\),则区间 \([l,r]\) 的贡献即 \(pre[r] - pre[l] + a[l] = pre[r] + (a[l] - pre[l])\),如果直接暴力那没得说,但是直接暴力显然不能快速维护,快速维护就必须知道具体的第 \(k\) 位为 \(1\) 的条件,不能涉及位运算
若 \(a[l] - pre[l] > 0\) 那么上述式子可以转化为 \(a + b\) 的形式,这个就很好判断了,令 \(a\%2^{k+1} \to a,b \% 2^{k+1} \to b\),然后如果第 \(k\) 位为 \(1\) 那么 \(a+b\) 的值就一定在某个范围内,具体就是 \([2^k,2^{k+1}-1]\) 和 \([2^{k} + 2^{k+1},2^{k+2}-1]\),这个自己转成二进制是很好列的。
若 \(a[l] - pre[l] < 0\) 那么上述式子可以转化为 \(a - b\) 的形式,此时就考虑分类讨论,令 \(a \% 2^k \to a',b \% 2^k \to b'\),则若 \(a\) 的第 \(k\) 位为 \(1\),满足下面两个条件之一之差第 \(k\) 位也为 \(1\),\(b\) 的第 \(k\) 位为 \(1\) 且 \(a' < b'\) 或 \(b\) 的第 \(k\) 位为 \(0\) 且 \(a' \ge b'\)。当 \(a\) 的第 \(k\) 位为 \(0\) 则情况相反。
上述的式子都可以用线段树快速维护。
代码:
(不放线段树的那样被理解起来太抽象了,就放个暴力)
点击查看代码
#include<bits/stdc++.h>
#define int long long
#define PII pair<int,int>
using namespace std;
const int N = 2e3+5;
const int MOD = 998244353;
const int INF = 1e9+5;
struct node{
int l,r,id;
}p[N];
int a[N],b[N],sz,L[N],R[N],ans[N],ed[N],pw[60],pre[N];
priority_queue<PII> q;
PII c[N];
bool cmp(node a,node b){
return a.l < b.l;
}
int power(int a,int b){
int res = 1;
while(b){
if(b & 1) res = res * a % MOD;
a = a * a % MOD;
b >>= 1;
}
return res;
}
int query(int l,int r){
if(l > r) swap(l,r);
int pos = INF;
for(int i=1; i<=sz; i++){
if(l <= c[i].first && c[i].first <= r){
pos = min(pos,c[i].second);
}
}
return pos;
}
bool chk(int a,int b,int k){ //判断 a + b 第 k 位是否为 1,b 可能为负
if(b > 0){
a %= pw[k+1],b %= pw[k+1];
if(pw[k] <= a + b && a + b <= pw[k+1]-1) return true;
if(pw[k+1]+pw[k] <= a + b && a + b <= pw[k+2] - 1) return true;
return false;
}
else{
b = -b;
int pa = a & pw[k],pb = b & pw[k];
a %= pw[k],b %= pw[k];
if(pa){
if(pb && a < b) return true;
if(!pb && a >= b) return true;
}
else{
if(pb && a >= b) return true;
if(!pb && a < b) return true;
}
return false;
}
}
signed main(){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
int T;scanf("%lld",&T);
pw[0] = 1;
for(int i=1; i<=55; i++) pw[i] = pw[i-1] * 2;
while(T--){
int n,m;scanf("%lld%lld",&n,&m);
for(int i=1; i<=n; i++) scanf("%lld",&a[i]);
for(int i=1; i<=n; i++) scanf("%lld",&b[i]);
int tot = 0;
for(int i=1; i<=m; i++){
int l,r;scanf("%lld%lld",&l,&r);
p[++tot] = {l,r,i};
}
sort(p+1,p+tot+1,cmp);
for(int i=0; i<=50; i++){
sz = 0;
for(int l=1; l<=n; l++) pre[l] = pre[l-1] + b[l];
for(int l=1; l<=n; l++){
int tmp = a[l] - pre[l];
R[l] = INF;
for(int r=l; r<=n; r++){
if(chk(pre[r],tmp,i)){
R[l] = r;break;
}
}
}
int pos = 1;
for(int l=1; l<=n; l++){
while(p[pos].l == l && pos <= tot) q.push({p[pos].r,p[pos].id}),++pos;
while(!q.empty() && q.top().first >= R[l]){
ed[q.top().second] = (ed[q.top().second] + pw[i])%MOD;q.pop();
}
}
while(!q.empty()) q.pop();
}
int now = 233,ans = 0;
for(int i=1; i<=m; i++){
ans = (ans + ed[i] * now)%MOD;
now = now * 233 % MOD;
printf("%lld\n",ed[i]);
}
}
return 0;
}
双连通分量
大力推荐一篇blog,但是本文也不是直接抄的,只是借鉴了他的结论和结构。
下文不说明则只考虑无向连通图的相关性质。
先来一些定义:
割点:删去该点后,图的联通分量数会增加。
割边(桥):删去该边后,图的联通分量数会增加。
有了这个就能定义我们关键的东西了:
点双连通分量:一张图的极大的点双连通子图(不含割点的子图)
边双连通分量:一张图的极大的边双联通子图(不含割边的子图)
点双连通分量以及边双连通分量缩点后都为一棵树,而有向图的强连通分量缩点后为一个 DAG,其中点双连通分量缩点后的结果就是圆方树。
下面就是研究他们对应的一些性质,研究完了性质才能谈高效地维护。
点双连通分量
删去割点之后不连通的两个点之间的所有路径必然经过割点,所以可以以"必经点"来理解割点这个概念,所以可以导出如下结论:
- 任意两点之间的路径上的割点就是两点之间路径的必经点
对于两个点双其不满足传递性,即不存在若 A,B 点双连通,B,C 点双连通,则 A,C 点双连通,因为可能存在同一个点同时位于相交的两个点双里,比如一个 "8" 字形。对于任意两个点双不可能交于两个点,因为这样对于两个点双内的点相当于可以导出两条不经过重复点的路径,两个点双可合并为更大的一个点双。而如果相交于一点,则我们尝试将这个点删去,如果删除之后两个点双仍联通则意味着我们应该在一开始就让两个点双合并为一个点双,因此得到这个点必然是割点。所以可以导出如下结论:
- 两个点双如果有交,必然只会交于一点且交点一定为割点
上文我们推得:两个点双交点必然是割点,但是割点一定是两个点双的交点吗?
这里需要区分的一点:割点是指的删除之后将原图分为了若干连通分量,但是当我们只关心包含它的某一个点双时,这个割点就变成了非割点,因为即使删去这个点对于点双依旧联通
考虑割点的两个邻居节点 \(u,v\),则删去割点后 \(u,v\) 必然不连通,显然 \(u,v\) 不能位于同一个点双,因为若其位于同一个点双则不应存在删除一个点后 \(u,v\) 不连通。
所以相当于 \(u,v\) 分属于两个点双,而因为两点一线的图根据我们的定义为点双连通图,所以相当于我们的割点与 \(u,v\) 均点双连通。所以可以导出如下结论:
- 一个点是割点当且仅当该点同时包含于超过 \(1\) 个点双,由一条边连接的两个点满足点双连通
考虑对于一个点双中的点 \(x\),一定满足 \(deg_x > 1\)(其中 \(deg_x\) 代表点 \(x\) 的度数),因为若其度数为 \(1\) 则必然无法导出两条不经过重复点的路径。设 \(x\) 的两个相邻节点 \(u \not= v\),则我们将 \(u,v\) 之间不经过 \(x\) 的路径拿出来接上 \(x\) 则形成了一个经过 \(x\) 的简单环。当然对于两点一线图就不存在这种情况。所以可以导出如下结论:
- 对于 \(n \ge 3\) 的点双中的任意一点,必然存在经过该点的简单环。
边双连通分量:
考虑割边两侧的点 \(u,v\),如果删除割边则 \(u,v\) 一定不连通,也就是可以将割边理解为必经边,所以可以导出如下结论:
- 任意两点的路径上的割边,就是两点的路径的必经边
每断开一条割边,原本的连通块就会分裂为两个连通块。当我们断开所有割边时,图被分裂为了 割边数加 \(1\) 个连通块,且每一个连通块内都不含割边并且也是极大的,也就是每一个连通块都是一个边双。综上我们的边双之间肯定是通过割边相连接的,缩点之后就可以形成下图的形式:
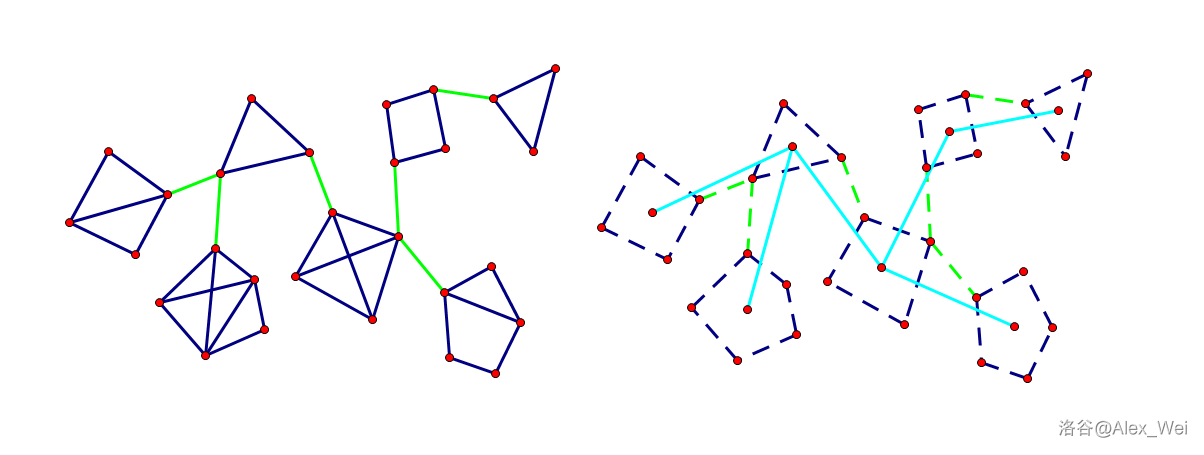
(图片为复制过来的)
也就是说任意两个点路径的必经边其实就是对应树上两点路径所经过的边。可以发现,在任意两个边双之间连接一条边,都会使得缩点后的树形成一个环,也就是说原来的割边不再是割边了,这些边双就被缩起来了。
对于任意两个边双都不存在交点,每个点都只属于一个边双,因为边双之间均通过割边连接,因此:
- 边双具有传递性,即若 A,B 边双联通,B,C 边双联通,则 A,C 边双连通
每一个边双内部无割边,因此:
- 对于同一个边双内的两个点 \(u,v\),必然满足 \(u,v\) 边双联通
在边双中,对于一条边 \((u,v)\),将其删除后 \(u,v\) 之间必然仍存在路径相连,所以将这条边与该路径拼在一起就形成了一个环,因此:
- 对于点双内的任意一条边 \((u,v)\) 必然存在经过 \((u,v)\) 的环,对于一个点双内的点 \(u\) 必然满足存在经过 \(u\) 的环
通过上述分析可以发现点双连通比边双连通要强,也就是可以通过点双连通推出边双联通。
tarjan 求割点
我们不妨记录点 \(x\) 在 DFS 树上的子树为 \(T(x)\),则令 \(T'(x) = V\setminus T(x)\),即除了其子树以外的部分。
对于非 DFS 树根节点:
这个点 \(x\) 是割点就是相当于删除 \(x\) 之后有 \(x\) 的一些子树不与 \(x\) 的父亲联通了,因为是树,所以不同的子树之间一定不连通。
不连通其实就是相当于 \(x\) 的某一棵子树不能通过非树边到达 \(x\) 的父亲,因为非树边只可能是祖先边。
所以我们可以考虑设 \(low_u\) 表示节点 \(u\) 通过树边和非数边到达的点里最小的 \(dfn\) 序,这样不连通就意味着存在 \(u \in T(x),low_u \ge dfn_x\)
也就是可以导出如下结论:
- 对于一个非根节点 \(x\),其为割点当且仅当存在其存在子树内的一点 \(y\) 满足 \(low_y \ge x\)
对于 DFS 树根节点:
只要该点子树大于 \(1\) 个即可,因为这样删去之后子树之间一定不联通。否则如果只有一个子树,删除之后子树内部依旧可以通过树边联通。
代码如下:
点击查看代码
#include <bits/stdc++.h>
using namespace std;
constexpr int N = 1e5 + 5;
int n, m, R;
int dn, dfn[N], low[N], cnt, buc[N];
vector<int> e[N];
void dfs(int id) {
dfn[id] = low[id] = ++dn;
int son = 0;
for(int it : e[id]) {
if(!dfn[it]) {
son++, dfs(it), low[id] = min(low[id], low[it]);
if(low[it] >= dfn[id] && id != R) cnt += !buc[id], buc[id] = 1;
}
else low[id] = min(low[id], dfn[it]);
}
if(son >= 2 && id == R) cnt += !buc[id], buc[id] = 1;
}
int main() {
cin >> n >> m;
for(int i = 1; i <= m; i++) {
int u, v;
cin >> u >> v;
e[u].push_back(v), e[v].push_back(u);
}
for(int i = 1; i <= n; i++) if(!dfn[i]) R = i, dfs(i);
cout << cnt << endl;
for(int i = 1; i <= n; i++) if(buc[i]) cout << i << " ";
return 0;
}
tarjan 求割边
其实用 tarjan 求割点和割边是差不多的。
就是考虑当 \(low_u = dfn_x\) 时,\(x\) 其实是一个割点,但是相连的边是割边吗,显然不是,都形成一个环了。
树上差分求割边
对于一个 DFS 树来说,割边必然是树边,那么对于树边来说它是割边当且仅当不存在非树边使得其包含这个树边。
也就是对于每一条非树边使用树上差分的方法找到其覆盖的树边,将这些边标记为非割边,最后剩下的就是割边。
圆方树
介绍和构造:
圆方树的本质就是点双的缩点,在圆方树中我们可以很好地保留原图中必经点的信息,对于处理仙人掌的问题也常用圆方树。
其过程也与边双的缩点类似,求出每个点双具体的状态然后缩点,但是因为可能存在一个点位于多个点双中的情况,所以并不能直接连,所以就有一种巧妙的方式:对于每一个点双建立一个方点,对于原图上就有的点我们称之为圆点,对于每一个点双我们从其对应的方点向其内部包含的所有圆点连边,这就构成了一棵圆方树。
其实就是将每一个点双缩成一个菊花,然后用割点连接各个菊花,因为在点双中割点就可以理解为分界点,所以连接形成的结构必然是一棵树。
具体构造的代码实现与求割点类似,但是在我们弹栈的时候不能把割点也弹了,因为一个割点可能位于多个点双中。
代码:
点击查看代码
void tarjan(int id) {
dfn[id] = low[id] = ++dn, stc[++top] = id;
for(int it : e[id]) {
if(!dfn[it]) {
tarjan(it), low[id] = min(low[id], low[it]);
if(low[it] >= dfn[id]) {
g[++node].push_back(id), g[id].push_back(node);
for(int x = 0; x != it; )
g[node].push_back(x = stc[top--]), g[x].push_back(node);
}
}
else low[id] = min(low[id], dfn[it]);
}
}
性质:
这些性质都是在描述:圆方树毫无保留地记录了原图的必经性,一般当要求必经性或者两点间路径上所有点的信息常用圆方树。
说通俗一点就是:圆方树路径上的圆点为两点路径的必经点,路径上的方点下的圆点就是两点路径的可经过的点。
- 性质 1:圆点 \(x\) 的度数等于包含它的点双个数
证明:显然 - 性质 2:圆方树上圆方点相间
证明:显然 - 性质 3:圆点 \(x\) 是叶子当且仅当其在原图上是非割点
证明:每一个割点必然连接两个或以上的点双,因为每一个点双对应圆方树上的一个菊花,也就是它在圆方树上必然连接两个或以上的点,得证。 - 性质 4:在圆方树上删去 \(x\) 后的连通性与在原图上删去 \(x\) 后的连通性相同。
证明:若 \(x\) 不为割点,则显然不会对连通性产生贡影响;若 \(x\) 为割点,则对于不同点双之间连通性的影响也显然是一样的。 - 性质 5:\(x,y\) 在圆方树上简单路径上的圆点对应其原图上 \(x,y\) 之间的必经点
证明:根据性质 4 可知,当我们删去路径上任意一个圆点其在圆方树上就不连通,即其在原图上也不联通,而当我们删除非路径上的圆点不会对它们的连通性产生影响,得证。
虚树
虚树一般用于树上给定一些关键点集合,而且对于集合大小之和有一定的限制,这样就可以只保留关键的一些节点而忽略无用的点。
用一道经典的题作为引入:SDOI2011消耗战
一个显然的 \(dp\) 就是,设 \(f[i]\) 表示 \(i\) 与其子树内的询问点均不联通的最小代价,转移就是枚举与儿子的边断或不断,即:
这样做一次的复杂度为 \(O(n)\) 再来 \(q\) 次询问复杂度就炸了。但是我们考虑其实我们没有必要每个都转移,考虑对于一条链,如果其上不存在询问点,那么我们显然可以直接将这一条链缩成一条边,以及如果一棵子树内没有询问点,显然也可以直接将这棵子树缩成一个点,我们的虚树就应运而生。
一棵树+若干的询问点构成的虚树就是:询问点+询问点两两之间的 \(lca\) 构成的树。
这棵树的大小为 \(O(询问点个数)\),那么我们就可以直接在这棵树上 \(dp\) 然后就可以直接通过本题了。
现在还剩下一个很大的问题就是如何建树。
常用的构造方式:
将询问点按 \(dfs\) 序排序,模拟 dfs 的过程采取增量法插入,即用栈从栈底到栈顶维护虚树上一条自上而下的链。设插入点为 \(i\),栈顶点为 \(t\),栈顶的下一个点为 \(t_2\),\(d = lca(i,t)\)(注意 \(d\) 在下文的操作中不会改变)。
- 若 \(dep_d \le dep_{t_2}\) 则 \((t,t_2)\) 之间一定有连边,连边,然后弹栈,直到该条件不满足或栈的大小小于 \(2\)
- 接下来若 \(d \not= t\) 则意味着 \(dep_d < dep_t\)(根据过程可知此时 \(t_2\) 是第一个小于 \(dep_d\) 的,所以 \(t\) 只可能等于或者大于,如果 \(t \not= d\) 也就意味着大于),即 \(t\) 和 \(i\) 位于 \(d\) 的两个不同子树内,此时可以将 \(t\) 弹出,连边 \((d,t)\) 且 \(d\) 入栈。否则如果 \(d = t\) 则什么都不做
- 将 \(i\) 入栈
- 当重复前三步执行完毕后,要将栈里剩余的相邻节点连边。
需要注意的是我们需要在每组询问都清空邻接表,但是显然全清就炸了,所以考虑直接存下虚树到底有哪些点,然后询问结束后把使用的点全部清空就好了。
清空依旧坚持原则:清空我们使用的,而不是清空我们需要用的。(因为有的时候估计不准我们需要用什么)
时间复杂度的瓶颈在于按 \(dfs\) 序排序,求 \(lca\) 显然可以优化到 \(O(1)\)。
代码(不要忘记询问完了之后清空):
点击查看代码
stc[top = 1] = p[1];
for(int i = 2; i <= k; i++) {
int d= lca(stc[top], p[i]);
while(top > 1 && dep[d] <= dep[stc[top - 1]]) trans(stc[top - 1], stc[top]), top--;
if(d != stc[top]) trans(d, stc[top]), stc[top] = d;
stc[++top] = p[i];
}
几个结论:
设询问为 \(a_0,a_{1},\ldots,a_{n-1}\),按 \(dfs\) 序排序之后则虚树的边权和即 \(\dfrac{\sum_{i=0}^n dis(a_i,a_{(i+1)\% n})}{2}\),证明可以使用 dfs 序的性质。
当我们建虚树是为了自底向上 \(dp\) 时,不需要显示建图,可以边建虚树边转移,因为我们虚树的建立顺序就是自底向上的顺序。
同余最短路
(仅包含一些基础介绍)
同余最短路解决的问题就是求解给定范围内有多少个数可以通过给定的数通过系数非负的线性组合得到。
解决的核心点在于:若 \(p\) 可以被表示出来,则 \(p + x\times a_i(x > 0)\) 也一定可以被表示出来。所以可以任找一个 \(a_i\) 的模其同余的同余类 \(K_j\),找到 \(K_j\) 中最小能被表示出来的元素 \(f_j\),则 \(K_j\) 中所有大于等于 \(f_j\) 的元素都可以被表示出来。
所以可以考虑选择其中最小的一个数 \(a_1\),得到某个同余类中最小能被表示出来的数,然后通过加 \(a_2,a_3,\ldots,a_n\) 转移到其他的同余类。
也就是我们可以将这个问题转化为一个图论模型,从 \(j\) 向 \((j + a[i]) \mod a_1\) 连边,边权为 \(a_i\),这样只需要从 \(0\) 开始跑一遍最短路得到的就是答案。
求出来了每一个 \(f\) 之后我们的问题就很好解决了。
而且这种题中 dijkstra 不一定比 SPFA 跑得快奥。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号