【学习笔记】字符串小总结
刷了两三周的字符串题,可以说对于这些字符串算法有了一个基本的了解了,大概包括从普及到省选的字符串算法。
1.哈希
1.1 算法基础:
我们一般写的哈希就是使用的指数的形式,因为这样很方便也很好写。
一般我们可以考虑递推处理出一段前缀的哈希值,而对于一个区间 也可以发现它的哈希值就是 。
我们指数形式的的哈希如果从左到右递推的话其实是越靠左边指数越大的。
1.2 算法应用:
1.2.1 字符串相同
不知道大家有没有和我一样的感觉:哈希总是写挂。
我们其实就自己背两个质数,一个质数当作字符集大小另一个质数当作模数,这样大概率是不会挂的。(备忘:,)
其实哈希的应用是很多的,其中最常见的肯定就是用于判断字符串是否相同,可以直接通过判断哈希值是否相同来判断,就方便很多了。
1.2.2 周期
哈希还有一点作用就是求字符串的循环节:
其实就是枚举循环节长度设为 ,判断 与 是否相同,如果要求完全覆盖那么就只需要使得枚举的 是字符串长度的约数就好了。
那么为什么可以这样判断呢?
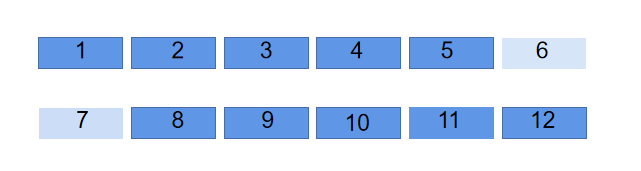
我们可以观察上面这个图,假设我们一个小方格代表一个循环节。
我们可以发现如果 和 相等,也就是可以推出来 ,同理得到 ,继续就可以得到 ,也就可以推出来一个小方格也就是我们枚举的长度是一个循环节。
1.2.3 经典应用
[NOI Online 2021 提高组] 积木小赛 可以用来练练哈希判断字符串相同。
也就是枚举 Bob 的每个左端点然后一点点扩展右端点,然后在 Alice 上贪心匹配。
2. Trie 树
2.1 算法基础:
Trie 树也就是将每一个字符串都插入进一个树形结构当中,对于每一个节点其代表的字符串就是从根到这个节点的路径上的字符顺次连接的结果。
所以每一个点都有字符集大小个儿子,代表在当前后面插入一个字符能转移到的点。
所以其实在 Trie 树上的点都代表某个字符串串的一个前缀。
2.2 算法应用:
2.2.1 基本性质
Trie 树一个很大的应用应该就是判断字符串是否存在了。
也就是我们给定很多的字符串,多次询问某个字符串是否出现过,使用 Trie 树复杂度就只是字符串长度的,而如果使用哈希就至少比这个要大。
Trie 树其实也可以考虑存下所有的字符串的信息,然后每个字符串去单独跑一遍就可以得到这个字符串与其他所有的字符串的某些关系了,这样可以讲复杂度优化到字符串长度。
2.2.2 Trie 树
Trie 树,也就是字符集只有 的 Trie 树,常常用于解决与异或或一些位运算有关的题。
2.3 模板实现:
点击查看代码
void insert(char *s,int p){
int n = strlen(s+1);
int now = rt;
for(int i=1; i<=n; i++){
if(!ch[now][s[i] - 'a']) ch[now][s[i] - 'a'] = ++tot;
now = ch[now][s[i] - 'a'];
}
}
3 Manacher
3.1 算法基础:
这也可以说是第一个比较厉害的字符串科技了。
Manacher 就是解决与回文子串相关的题,它可以以 (其中 是字符串长度)的时间求出 数组, 表示以 为回文中心的回文子串的半径的长度。
具体求法是很暴力的:确定每一个 的下界,然后暴力一点点增大 判断是否可行。
我们在求解的过程中是从前到后扫,在扫的过程中会动态维护两个值 ,其中 表示当前已知的回文子串的右端点最大的一个的右端点, 表示这个回文子串的中心。
假设我们现在所在的点是 ,我们可以发现如果 ,那么就意味着在当前的最长回文子串里一定可以找到一个点 与 对应,也就是 所处的位置是 完全翻过去的,所以此时也就是 ,可以结合下面这个图理解。
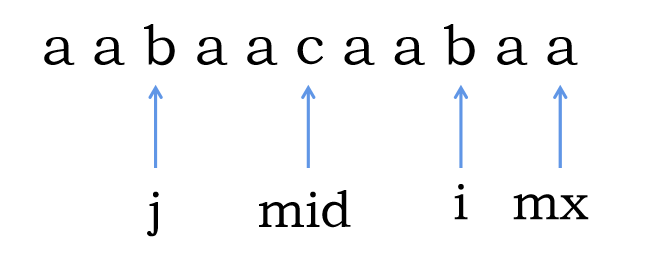
但是我们会发现这样不是很对,因为可能会出现这种情况:
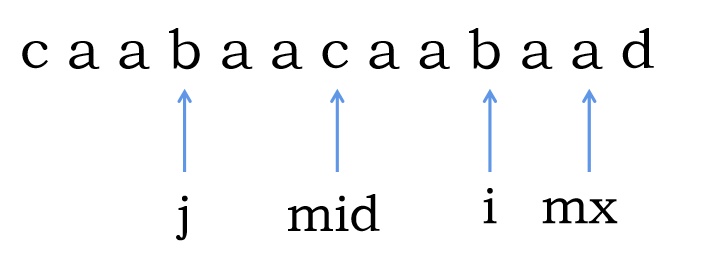
这个时候因为我们所在的最长回文子串能做到的只是保证 这个长度是回文的,更多就不确定了。
所以其实最终是
稍微观察一下就可以发现:,所以
这样我们会发现其实还是有问题的,因为我们只可以判断长度为奇数的回文串,因为我们是确定了某个点为中心,而长度为偶数的没有中心,怎么办?
我们在每个字符中间都插入一个字符集之外的字符,这样偶数的回文串也就可以理解为以这个字符为中心的字符串。
大概就是下面这样的变化(我的惯用写法):
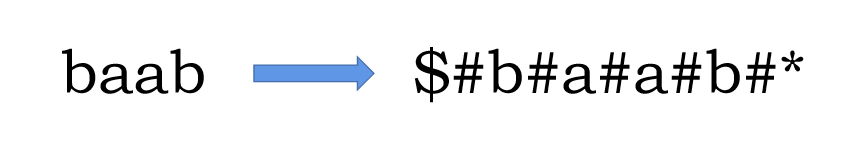
3.2 算法应用:
3.2.1 基本性质
将 数组每次减 也就是可以得到原串的所有回文子串。
3.2.2 经典应用
回文匹配 可以说很考察对于 Manacher 的理解。
显然我们可以先做一遍 KMP 求所有的出现位置,然后就可以转化为求区间和了。
显然我们需要做一下前缀和,难道我们要一点点减 数组吗?这就是 的了。
所以考虑贡献是什么样子的:, 就是前缀和数组,所以对于前缀和数组再做一次前缀和就好了。
3.3 模板实现:
点击查看代码
s[++tot] = '$';
for(int i=1; i<=n; i++) s[++tot] = '#',s[++tot] = tmp[i];
s[++tot] = '#';s[++tot] = '*';
int mx = 0,mid = 0;
for(int i=1; i<=tot; i++){
if(i <= mx) r[i] = min(mx - i,r[2 * mid - i]);
while(i > r[i] && i + r[i] < tot && s[i - r[i]] == s[i + r[i]]) r[i]++;
if(i + r[i] - 1 > mx) mx = i + r[i] - 1,mid = i;
}
4 KMP
4.1 算法基础:
我们首先定义:若对于一个字符串 ,使得它的一个真前缀 同时也是它的真后缀,那么就称 是 的一个 。
对于 例如:对于 , 就是他的一个 ,因为 既是它的前缀也是它的后缀
定义 数组: 表示原串 这个前缀的最长 的长度
对于 数组的求法,其实也非常的暴力:
我们会动态维护 表示当前的 值,每次比较 和 是否相同,如果相同则匹配成功,如果不同则令 然后继续进行匹配。
前面非常好理解,就是后面有点难以理解,为什么失配的时候应该让 呢?
我们首先要知道,当我们匹配到 这一位的时候 其实存的是 ,我们可以发现如果失配那么下一个最长的可能可以继续匹配的是 ,结合下图来理解:

我们当前匹配好了 发现下一个 失配了,那么就跳 ,跳到 就可以匹配了。
这其实是因为我们跳 就相当于找到了一个新的最长的既是前缀又是后缀的字符串,拿这个去匹配如果成功的话显然这就是目前最优的答案,因为我们的 要求既是前缀又是后缀显然如果可以匹配同时加一个字符也是满足条件的。
因为我们每跳一次 至少向前移动 ,而我们最多向后移动 次,所以复杂度就是 的。
4.2 算法应用:
4.2.1 字符串匹配
对于 KMP 一个经典的应用就是以 是时间进行字符串匹配。
也就是求解较短串的 数组,用较短串与较长串以类似 KMP 的形式进行匹配。
4.2.2 周期
对于 KMP 还有一个很好用的性质就是求解周期:对于一个长度为 的字符串,它的最短周期就是 ,这里的周期并不意味着一定恰好完全覆盖,就是例如: 的周期就是 。
证明可以类似上文哈希求解循环节的证明,大体思路一致。
4.2.3 经典应用
CF526D Om Nom and Necklace 如果搞懂了这个题应该对 KMP 的理解就会更深一点。
显然令 ,那么 一定占据整数个周期,而且 肯定是尽可能多地分这些周期,所以我们直接求出来周期数就可以算出来 的大小,那么剩余的字符的个数就是 的大小,判断一下是否有 就好了
4.3 模板实现:
点击查看代码
nxt[1] = 0;
for(int i=2,j=0; i<=n; i++){
while(j && s[j+1] != s[i]) j = nxt[j];
if(s[j + 1] == s[i]) j++;
nxt[i] = j;
}
5 exKMP(Z-function)
5.1 算法基础:
其实我感觉这个东西叫 exManacher 还差不多,因为求解方法很像。
这个东西可能别名也叫做 ,具体就是求解一个 数组。
其中 代表 这个后缀与整个字符串的最长公共前缀,例如 其中 。
在求解过程中我们会从前到后扫一遍,并且动态维护 ,其中 代表 , 就是这个式子对应的 。
具体如何求解我们可以结合下图来考虑:
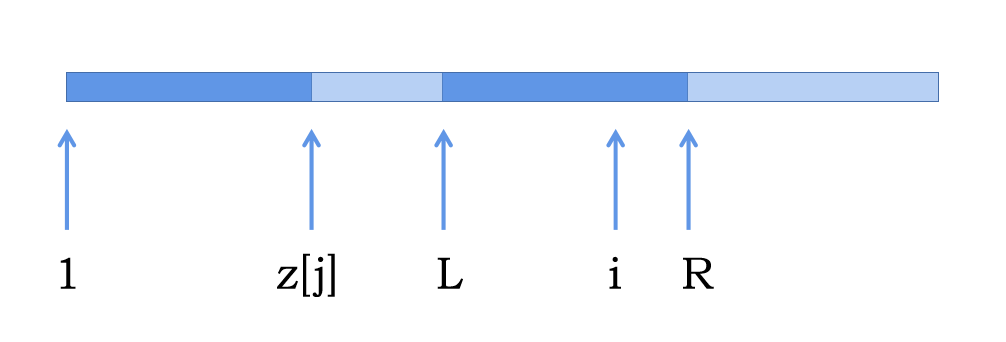
我们设 ,这里的 也就是上文的 , 也是上文的 。
我们知道两段深蓝色的是完全相同的部分。
而对于 我们其实可以在 中找到一个与之对应的点,也就是 ,可以理解为将 平移了 ,所以 就平移到了 。
那么显然 ,但是依旧因为我们的这一部分只保证了对于 这一段是相同的,所以应该取 ,也就是最终的式子就是:
5.2 算法应用:
5.2.1 周期
它也可以用来解决周期类的问题,而且有的时候更加方便,因为我们可以限制周期出现多少次。
对于判断周期,我们就可以枚举周期长度,设为 ,然后理解为每 个设置一个点,判断这些点与整个串的最长公共前缀的长度是否大于等于 ,就可以得到是否是周期。
可以结合下图理解:

5.2.2 经典应用
感觉比较有启发式的应用也就是 [NOIP2020] 字符串匹配 了。
显然可以类比于周期,因为我们如果令 那么 就是 的周期。
那么直接枚举 长度然后直接枚举周期个数,然后一个个递推判断,复杂度 可以通过这个题。
5.3 模板实现:
点击查看代码
z[0] = 0,z[1] = n;
int l = 0,r = 0;
for(int i=2; i<=n; i++){
if(i <= r) z[i] = min(r - i,z[i - l + 1]);
while(i + z[i] <= n && s[i + z[i]] == s[z[i] + 1]) z[i]++;
if(i + z[i] - 1 > r) r = i + z[i] - 1,l = i;
}
6 AC自动机(ACAM)
6.1 算法基础:
AC 自动机其实就是 Trie 树上多了一个 树。
对于 它代表的是 这个状态的最长的后缀所代表的状态且满足这个后缀在 AC 自动机里出现。
看上去很绕口,其实就是在它前面删除一些字符,使得删的字符数最少,并且删完之后的状态在 AC 自动机里出现。
对于 树的构建可以类比 KMP 算法,也就是 ,我们构建的过程一般是使用 BFS 来完成。
但是我们也会发现(至少在我的代码里),我们也会连一些奇奇怪怪的 ,以及一些节点的儿子会指向一些奇怪的节点,因为我们 AC 自动机的 Trie 树大概率是用来字符串匹配的,所以我们这里其实是提前为失配做好了准备,可以使得失配之后匹配的更快一点。
6.2 算法应用:
6.2.1 基本性质
AC 自动机最重要的就是他的 树的性质(因为 Trie 树大家肯定都会)
做 AC 自动机的题一定要牢记一点:不大用考虑失配,相信自己,失配之后跳 一定没错。
毕竟这个东西不记住到时候现推比较麻烦。
对于 AC 自动机它的状态也就是节点是一个非常好的量,是很适合放到 的状态里的,所以 AC 自动机常常会与 一起考察。
AC 自动机和 SAM 最大的区别就是:SAM 大部分是对于一个字符串的操作,而 AC 自动机大多数是多个字符串之间的匹配等等。
便于应用的性质:
- 对于 AC 自动机上的每一个节点,它在 fail 树上的所有父亲,就是出现过的它的所有后缀。
- 跳 fail 相当于跳 border,而因为 border 的 border 也是它的 border,所以其实我们不断跳 相当于取得所有的 border
6.2.2 经典应用
一个非常经典的应用就是 [NOI2011] 阿狸的打字机,也就是给定几个字符串,多次询问一个字符串在另一个字符串中的出现次数。
这一类题都非常典型,就以这个题为例来看看转化过程。
首先我们要知道一个很关键的性质:若字符串 在字符串 出现,也就意味着 可以表示为 的某一个前缀的后缀。
其实这个东西在 AC 自动机上很好体现,就是对于 我们先在 Trie 树上跑也就是求每一个前缀,然后再对于每一个跑到的位置将它在 树上到根的路径上经过的点的权值和都加一,也就是找到这个前缀出现过的所有的后缀,这样我们只需要将 在 Trie 树上跑一遍最后跑到的位置的权值就是答案。
可以显然使用树剖维护,但是这样不是很优,因为存在路径修改所以复杂度是 。
我们可以考虑对于 的每一个前缀我们只将这个前缀的节点权值加一,这样将 在 Trie 树上跑一遍之后就直接查询子树和就好了。
这样就不需要树剖了,只需要维护一下 序,就可以转化为单点修改、区间查询了。
当然对于这个题可能需要离线一下操作,不然直接暴力搞复杂度有点高。
6.3 模板实现:
点击查看代码
void insert(char *s){ //Trie 树插入 s 这个字符串
int n = strlen(s + 1);
int now = rt;
for(int i=1; i<=n; i++){
if(!ch[now][s[i] - 'A']) ch[now][s[i] - 'A'] = ++tot;
now = ch[now][s[i] - 'A'];
}
flag[now] = true;
}
void build(){ //构造 fail 数组
queue<int> q;
for(int i=0; i<ALP; i++){
if(ch[rt][i]){
fail[ch[rt][i]] = rt;
q.push(ch[rt][i]);
}
else ch[rt][i] = rt; //方便失配的时候用
}
while(!q.empty()){
int now = q.front();q.pop();
for(int i=0; i<ALP; i++){
if(ch[now][i]){
fail[ch[now][i]] = ch[fail[now]][i]; //类似 KMP
q.push(ch[now][i]);
}
else ch[now][i] = ch[fail[now]][i]; //方便失配的时候用
}
}
}
SA
算法简介
SA 会维护两个数组 与 。
其中 表示排名为 的后缀的第一个元素的下标, 表示后缀 的排名。
以 banana 为例来理解这两个数组的含义:
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| b | a | n | a | n | a | |
| 6 | 4 | 2 | 1 | 5 | 3 | |
| 4 | 3 | 6 | 2 | 5 | 1 |
算法流程
常用算法
考虑如何求解这两个数组:
朴素算法:对所有的后缀排序, 比较两个字符串的字典序,时间复杂度
优化算法:对于比较字典序我们使用二分与哈希来做到 ,这样总复杂度就降到了
倍增算法:使用倍增在 的时间内求解。
倍增算法
下面就着重考虑倍增算法:
我们的思想就是用桶排来得到后缀的排名,也就是说我们会进行 次桶排,其中第 次的桶排维护的就是长度为 的子串的 ,并用当前轮的 更新下一轮的 ,并用下一轮的 ,得到下一轮的 。
那么我们来考虑如何通过当前轮的 来获取下一轮的 值,假设我们当前处理的是长度为 的子串的 ,那么对于两个数
- 若 显然,的字典序在下一轮依旧小于
- 若 ,那么此时我们就比较 和 ,因为我们的前缀相等,那么就只能比后缀了。
那么显然这就是一个双关键字的排序,排序关键字分别为 ,那么排完序后就可以得到下一轮的 数组。
我们可以直接 sort 排序,但是这样的复杂度是 ,不过码量比较小。
当然我们也可以选择桶排,将总的复杂度优化为 。
这样求出来的是 数组,那么我们考虑如何通过 数组求出 数组,显然我们不可以直接 ,因为会出现相同,那也很好办就直接判断 与 所代表的二元组是否相等就好了。
下面就是关于桶排的过程:
因为我们这是双关键字排序,所以我们采取先排序第二关键字,然后用第二关键字的排序结果去用第一关键字更新。显然这样做是正确的。
H 数组
当然后缀数组的精髓不在 与 ,而是在于 数组。
我们定义 表示 与 的最长公共前缀(LCP)的长度,定义 表示后缀 与排名在其前面的后缀的 的长度。显然
下面依旧是以 banana 的例子来理解这两个数组。
| i | ||||||
|---|---|---|---|---|---|---|
| banana | 1 | 6 | 4 | 0 | 0 | a |
| anana | 2 | 4 | 3 | 1 | 3 | ana |
| nana | 3 | 2 | 6 | 3 | 2 | anana |
| ana | 4 | 1 | 2 | 0 | 1 | banana |
| na | 5 | 5 | 5 | 0 | 0 | na |
| a | 6 | 3 | 1 | 2 | 0 | nana |
| 即排序后的 的后缀。 |
类似于 Manacher 与 函数, 也可以考虑继承 的信息,可以感性理解为将最前的一个字符砍掉,也就是 ,然后确定了下界就暴力判就好了。
套路用法
求两个后缀的 LCP
设我们要求的两个后缀分别的是 ,不妨假设 ,那么我们的答案就是
7 后缀自动机(SAM)
7.1 算法基础:
SAM 是一个有限状态自动机,其可以接受字符串的所有子串。
具体 SAM 的板子就是背了,这里放一下我常用的板子,以及我记忆的方式。
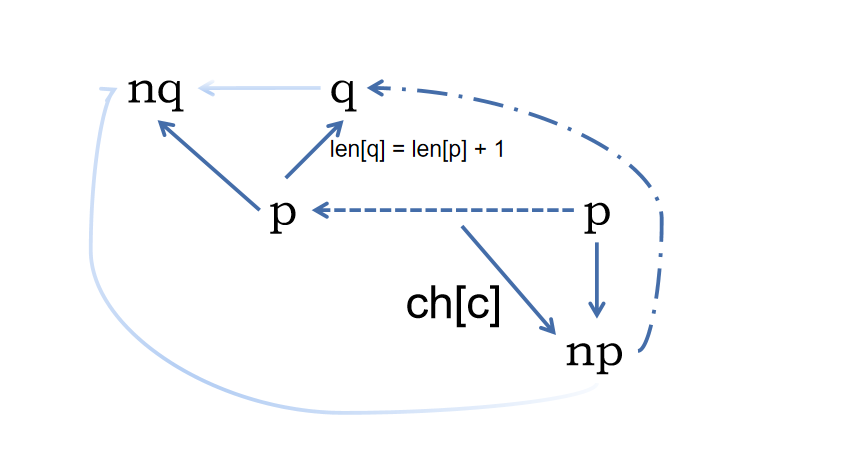
具体的话就是结合这个图来记忆,不然那些 这些很晕。
7.2 算法应用:
对于自动机也就是那些很奇妙的性质很有用了。
7.2.1
我们定义 表示字符串 在原串 中的所有出现位置的结束位置的集合。
对于一个 SAM 上的状态,其代表的就是 集合相同的子串,所以说 SAM 的每一个状态代表的是多个字符串。
那么也就是说对于两个不同的状态,其代表的子串一定不交。
而且对于一个状态其代表的字符串的长度一定是满的,也就是长度排序后一定是
对于 有几条很好用的性质:
- 若字符串 是字符串 的后缀,那么意味着 ,反之依然成立
- 对于任意两个没有后缀关系的字符串 ,必然有 ,反之依然成立
这样就意味着对于任意两个字符串 ,他们的 集合要么是包含关系,要么不交。
7.2.2 树
在 SAM 上也有一个树的结构,有人叫它 树,我这里就叫做 树了。
对于点 , 连接的点是 代表的最长的子串的一个后缀,满足这个后缀的 集合与 的 集合不同。
因为这个后缀可能会在其他的当前串没有出现的地方出现。
所以对于一个子串我们在 树上跳就相当于对这个子串的后缀进行划分,具体可以理解为下图的样子:

所以说我们设 表示 这个状态的最长子串,那么 这个状态代表的子串数量就是 。
7.2.3 其他性质
由以上的性质其实我们可以发现:对于状态 的 集合就应该等于他在 树上的儿子的 集合的并。
因为其实我们发现沿着 树上跳就是删除前面的字符,而沿着 树下跳,就应该是在前面加入字符,所以其实上面这种少了一个情况:当前节点代表的子串中存在原串的前缀,那么这个时候 集合应该新加入这个前缀的结束位置。
我们显然在前缀的前面添加字符是没啥用的,所以这个信息没办法传递给儿子。
大多数情况下我们只需要维护 集合的大小,那么直接加就好了,但是有的时候我们也需要维护具体是什么,那么就直接上一个线段树合并就好了。
对于 树还有一个性质:对于两个前缀 ,他们最长公共后缀,就是他们在 树上的 代表的最长子串。
关于后缀数组(SA),因为后缀数组的题 SAM 基本都可以做,就暂时不提后缀数组了。
对于 SAM 还有一个应用就是广义 SAM,也就是支持插入多个串,也与 SAM 非常类似就不说了。
便于应用的性质:
- 若 为 在 parent 树中的对应的子孙节点,那么必然有 代表的所有的串是 代表的所有的串的后缀
7.3 模板实现:
SAM 的构造是在线的,也就是每次新插入一个字符。
点击查看代码
void extend(int c,int pos){
int p = last,np = last = ++tot;sz[tot] = 1;val[tot] = a[pos];
mx[tot][0] = mn[tot][0] = val[tot];
len[np] = len[p] + 1;
for(;p && !ch[p][c]; p = fa[p]) ch[p][c] = np; //类似图上一直向右走 np
if(!p) fa[np] = 1;
else{
int q = ch[p][c]; //图中的 q
if(len[q] == len[p] + 1) fa[np] = q; //满足条件
else{
int nq = ++tot;
cop(nq,q);len[nq] = len[p] + 1; //新建节点
fa[q] = fa[np] = nq; //新建 fa 和 ch
for(;p && ch[p][c] == q; p = fa[p]) ch[p][c] = nq;
}
}
}





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 无需6万激活码!GitHub神秘组织3小时极速复刻Manus,手把手教你使用OpenManus搭建本
· C#/.NET/.NET Core优秀项目和框架2025年2月简报
· Manus爆火,是硬核还是营销?
· 一文读懂知识蒸馏
· 终于写完轮子一部分:tcp代理 了,记录一下