【题解】网络流 24 题

因为我比较菜，所以暂时 \(24\) 题并不全，只有一部分
题目做法中只讲解这个题目如何去做，具体证明见本文的末尾。

题目做法：

飞行员配对方案问题

题目分析：

显然这是一个二分图最大匹配问题。
对于这类问题我们一般会建立源点 \(s\) 和汇点 \(t\)，从 \(s\) 向二分图的一个点集连边，边的容量为 \(1\)，从 \(t\) 向二分图的另一个点集连边，边的容量为 \(1\)，而对于一个可行的匹配，就相当于二分图上的一条边，边的容量为 \(1\)。
那么我们的最大的匹配数量，也就是这个网络上的最大可行流的流量。

我们考虑我们的任意一个可行流是否可以对应着一种匹配的方案。显然可以，在残量网络中若边 \((u,v)\) 的剩余流量为 \(0\)，则意味着 \(u\) 与 \(v\) 匹配，这样我们就将一个可行流转化为了一种匹配的方案。
我们考虑任意一种匹配方案是否对应一个可行流。若 \(u,v\) 匹配，则意味着边 \((u,v)\) 流过了一点的流量，因为每个点只有可能与一个点匹配，所以满足容量限制，也显然满足流量守恒。

考虑这两者的大小关系：显然最大流的大小就是匹配的数量。

代码：

点击查看代码 
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1005;
const int MAXM = 20005;
const int INF = 1e8+5; 
struct edge{
	int nxt,to,val;
	edge(){}
	edge(int _nxt,int _to,int _val){
		nxt = _nxt,to = _to,val = _val; 
	}
}e[MAXM];
int n,m,s,t,cnt = 1,head[MAXN],cur[MAXN],dis[MAXN];
bool vis[MAXN][MAXN];
void add_edge(int from,int to,int val){
	e[++cnt] = edge(head[from],to,val);
	head[from] = cnt;
	e[++cnt] = edge(head[to],from,0);
	head[to] = cnt;
}
bool bfs(){
	memset(dis,-1,sizeof(dis));
	queue<int> q;
	q.push(s);dis[s] = 1;cur[s] = head[s];
	while(!q.empty()){
		int now = q.front();q.pop();
		for(int i=head[now]; i; i = e[i].nxt){
			int to = e[i].to;
			if(e[i].val && dis[to] == -1){
				dis[to] = dis[now] + 1;
				cur[to] = head[to];
				if(to == t)	return true;
				q.push(to);
			}
		}
	}
	return false;
}
int dfs(int now,int limit){
	if(now == t)	return limit;
	int flow = 0;
	for(int i = cur[now]; i && flow < limit ; i = e[i].nxt){  //注意当前弧优化 
		cur[now] = i;
		int to = e[i].to;
		if(e[i].val && dis[to] == dis[now] + 1){  //注意加分层图 
			int h = dfs(to,min(e[i].val,limit - flow));
			if(!h)	dis[to] = -1;
			e[i].val -= h;e[i^1].val += h;flow += h;
		}
	}
	return flow;
}
int dinic(){
	int ans = 0 ,flow;
	while(bfs())	while(flow = dfs(s,INF))	ans += flow;
	return ans;
}
int main(){
	int m,n;
	scanf("%d%d",&m,&n);
	s = n + 1,t = n+2;
	while(1){
		int from,to;
		scanf("%d%d",&from,&to);
		if(from == -1 && to == -1)	break;
		if(!vis[from][to])
			add_edge(from,to,1);
		vis[from][to] = true;
	}
	for(int i=1; i<=m; i++){
		add_edge(s,i,1); 
	}
	for(int i = m+1; i<=n; i++){
		add_edge(i,t,1);
	}
	printf("%d\n",dinic());
	for(int i=1; i<=m; i++){
		for(int j=head[i]; j; j = e[j].nxt){
			if(e[j].val == 0 && e[j].to != s && e[j].to != t){
				printf("%d %d\n",i,e[j].to);
				break; 
			}
		}
	}
	return 0;
}

试题库问题

题目分析：

我们考虑将原图分为两个点集：试题、类型。
有一个显然的建图：
从源点 \(s\) 向每一个试题连边，边的容量为 \(1\)，表示这种试题只可以选择一个。每一个试题向它所属的类型连边，边的容量为 \(1\)，表示这种试题只能选择一种类型。每一种类型向汇点 \(t\) 连边，边的容量为这种类型的需求量。
显然如果可以保证在汇点处满流，即流量大小为连向汇点的边的容量的和的话，即有解，否则就无解。

我们考虑对于任意一个可行流，其肯定对应着一种选择试题的方案，若试题 \(i\) 与类型 \(j\) 之间的边剩余流量为 \(0\)，即试题 \(i\) 选择作为类型为 \(j\) 的试题。
我们考虑对于任意一种选择试题的方案，也对应着一个可行流，因为每种试题只有一个且只会选择一个类型，所以满足容量限制与流量守恒。

代码：

点击查看代码 
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
const int M = 2e6+5;
const int INF = 1e9+5;
struct edge{
	int nxt,to,val;
	edge(){}
	edge(int _nxt,int _to,int _val){
		nxt = _nxt,to = _to,val = _val;
	}
}e[M];
int cnt = 1,S,T,head[N],cur[N],dis[N];
vector<int> v[N];
void add_edge(int from,int to,int val){
	e[++cnt] = edge(head[from],to,val);
	head[from] = cnt;
	e[++cnt] = edge(head[to],from,0);
	head[to] = cnt;
}
bool bfs(){
	memset(dis,-1,sizeof(dis));memcpy(cur,head,sizeof(head));
	queue<int> q;q.push(S);dis[S] = 1;
	while(!q.empty()){
		int now = q.front();q.pop();
		for(int i = head[now]; i; i = e[i].nxt){
			int to = e[i].to;
			if(dis[to] == - 1 && e[i].val){
				dis[to] = dis[now] + 1;
				q.push(to);
			}
		}
	}
	return dis[T] != -1;
}
int dfs(int now,int limit){
	if(now == T)	return limit;
	int flow = 0;
	for(int i = cur[now]; i && flow < limit;i = e[i].nxt){
		cur[now] = i;
		int to = e[i].to;
		if(dis[to] == dis[now] + 1 && e[i].val){
			int h = dfs(to,min(limit - flow,e[i].val));
			e[i].val -= h;e[i^1].val += h;flow += h;
			if(!h)	dis[to] = -1;
		}
	}
	return flow;
}
int dinic(){
	int ans = 0,flow;
	while(bfs()){
		while(flow = dfs(S,INF)){
			ans += flow;
		}
	}
	return ans;
}
int main(){
//	freopen("in.txt","r",stdin);
//	freopen("out.txt","w",stdout);
	int k,n;
	scanf("%d%d",&k,&n);
	S = k + n + 1,T = S + 1;
	int sum = 0;
	for(int i=1; i<=k; i++){
		int h;scanf("%d",&h);sum += h;
		add_edge(i+n,T,h);
	}
	for(int i=1; i<=n; i++){
		int sz;scanf("%d",&sz);
		for(int j=1; j<=sz; j++){
			int h;scanf("%d",&h);
			add_edge(i,h+n,1);
		}
		add_edge(S,i,1);
	}
	int ans = dinic();
	if(ans < sum){
		printf("No Solution!");
	}
	else{
		for(int i=2; i<=cnt; i+=2){
			int from = e[i^1].to,to = e[i].to;
			if(e[i].val == 0 && from != S && to != T){
				v[to-n].push_back(from);
			}
		}
		for(int i=1; i<=k; i++){
			printf("%d:",i);
			for(int j : v[i]){
				printf(" %d",j);
			}
			printf("\n");
		}
	}
	return 0;
}

圆桌问题

题目分析：

显然我们可以划分出两个点集：单位、餐桌。
因为每个单位的代表不希望在同一张餐桌，所以也就是每个单位向每个餐桌连边，容量为 \(1\)。因为每个单位与每张餐桌有人数限制，所以从源点 \(s\) 向每个单位连边，容量为该单位的人数，从每张餐桌向汇点 \(t\) 连边，容量为这张餐桌的人数限制。
显然最后若没有做到从 \(s\) 出发的边满流，即无解。

考虑任意一个可行流是否可以对应着一个选座的方案。若单位 \(i\) 与餐桌 \(j\) 之间的边有流量也就是意味着 \(i\) 单位有人坐在餐桌 \(j\)。
考虑一个选座方案是否对应一个可行流，显然以上面的方法也可以对应，也肯定会满足容量限制与流量守恒。

代码：

点击查看代码 
#include<bits/stdc++.h>
using namespace std;
const int INF = 1e8+5;
const int MAXN = 600;
const int MAXM = 1e5+5;
struct edge{
	int nxt,to,val;
	edge(){}
	edge(int _nxt,int _to,int _val){
		nxt = _nxt,to = _to,val = _val;
	}
}e[2 * MAXM];
int m,n,s,t,cnt = 1,head[MAXN],cur[MAXN],dis[MAXN];
void add_edge(int from,int to,int val){
	e[++cnt] = edge(head[from],to,val);
	head[from] = cnt;
	e[++cnt] = edge(head[to],from,0);
	head[to] = cnt;
}
bool bfs(){
	memset(dis,-1,sizeof(dis));
	queue<int> q;
	q.push(s);dis[s] = 1;cur[s] = head[s];
	while(!q.empty()){
		int now = q.front();q.pop();
		for(int i=head[now]; i; i = e[i].nxt){
			int to = e[i].to;
			if(e[i].val && dis[to] == -1){
				dis[to] = dis[now] + 1;
				cur[to] = head[to];
				if(to == t)	return true;
				q.push(to);
			}
		}
	}
	return false;
}
int dfs(int now,int limit){
	if(now == t)	return limit;
	int flow = 0;
	for(int i=cur[now];i && flow < limit;i = e[i].nxt){
		int to = e[i].to;
		cur[now] = i;
		if(dis[to] == dis[now] + 1 && e[i].val){
			int h = dfs(to,min(e[i].val,limit - flow));
			if(!h)	dis[to] = -1;
			e[i].val -= h;e[i ^ 1].val += h;flow += h;
		}
	}
	return flow;
}
int dinic(){
	int ans = 0,flow;
	while(bfs())	while(flow = dfs(s,INF))	ans += flow;
	return ans;
}
int main(){
//	freopen("in.txt","r",stdin);
//	freopen("out.txt","w",stdout); 
	int sum = 0;
	scanf("%d%d",&m,&n);
	s = n + m + 1,t = s + 1;
	for(int i=1; i<=m; i++){
		int r;
		cin>>r;
		sum += r;
		add_edge(s,i,r);
	}
	for(int i=1; i<=n; i++){
		int c;
		cin>>c;
		add_edge(i + m,t,c);
	}
	for(int i=1; i<=m; i++){
		for(int j=1; j<=n; j++){
			add_edge(i,j+m,1);
		} 
	}
	int ans = dinic();
	if(ans == sum){
		printf("1\n");
		for(int i=1; i<=m; i++){
			for(int j = head[i]; j; j = e[j].nxt){
				int to = e[j].to;
				if(e[j].val == 0){
					printf("%d ",to - m);
				}
			}
			printf("\n");
		}
	}
	else{
		printf("0\n");
	}
	return 0;
}

太空飞行计划问题

题目分析：

发现本题就是一个最大权闭合子图问题。
对于闭合图的定义：给定一个点集 \(V\)，若满足 \(V\) 中点的所有出边指向的点都在 \(V\) 中，那么就将点集 \(V\) 以及其中的所有出边称为一个闭合子图。
最大权闭合子图：所有的闭合图中，点权和最大的闭合图。

我们先将原图转化为流网络：
原图中的边正常连，容量为正无穷，从源点 \(s\) 向正权点连边，容量为这个点的权值，从负权点向汇点 \(t\) 连边，容量为这个点权值的相反数。
结论：最大权闭合子图的大小等于所有点权为正的点的点权和减去最小割的大小。

代码：

点击查看代码 
#include<bits/stdc++.h>
using namespace std;
const int MAXM = 1e6+5;
const int MAXN = 105;
const int INF = 1e9+5;
struct edge{
	int nxt,to,val;
	edge(){}
	edge(int _nxt,int _to,int _val){
		nxt = _nxt,to = _to,val = _val;
	}
}e[MAXM];
int cnt=1,s,t,head[MAXN],dis[MAXN],cur[MAXN];
bool bfs(){
	memset(dis,-1,sizeof(dis));memcpy(cur,head,sizeof(head));
	queue<int> q;
	q.push(s);dis[s] = 1;
	while(!q.empty()){
		int now = q.front();q.pop();
		for(int i = head[now]; i; i = e[i].nxt){
			int to = e[i].to;
			if(dis[to] == - 1 && e[i].val){
				dis[to] = dis[now] + 1;
				q.push(to);
			}
		}
	}
	return dis[t] != -1;
}
int dfs(int now,int limit){
	if(now == t)	return limit;
	int flow = 0;
	for(int i = cur[now]; i && flow < limit; i = e[i].nxt){
		int to = e[i].to;
		if(dis[to] == dis[now] + 1 && e[i].val){
			int h = dfs(to,min(limit - flow,e[i].val));
			e[i].val -= h;e[i^1].val += h;flow += h;
			if(!h)	dis[to] = -1;
		}
	}
	return flow;
}
int dinic(){
	int ans = 0,flow;
	while(bfs()){
		while(flow = dfs(s,INF)){
			ans += flow;
		}
	}
	return ans;
}
void add_edge(int from,int to,int val){
	e[++cnt] = edge(head[from],to,val);
	head[from] = cnt;
	e[++cnt] = edge(head[to],from,0);
	head[to] = cnt;
}
int main(){
	//freopen("in.txt","r",stdin);
	//freopen("out.txt","w",stdout);
	int n,m,k;
	int ans = 0;
	cin>>n>>m;  //太恶心了，读入是 m,n 
	s = n + m + 2,t = s + 1;
	for(int i=1; i<=n; i++){
		cin>>k;
		ans += k;
		add_edge(s,i + m,k);
		char tools[10000];
		memset(tools,0,sizeof tools);
		cin.getline(tools,10000);
		int ulen=0,tool;
		while (sscanf(tools+ulen,"%d",&tool)==1)//之前已经用scanf读完了赞助商同意支付该实验的费用
		{//tool是该实验所需仪器的其中一个      
		    add_edge(i + m,tool,INF);
		    if (tool==0) 
		        ulen++;
		    else {
		        while (tool) {
		            tool/=10;
		            ulen++;
		        }
		    }
		    ulen++;
		}
	}
	for(int i=1; i<=m; i++){
		cin>>k;
		add_edge(i,t,k);
	}
	ans = ans - dinic();
	for(int i=1; i<=n; i++){
		if(dis[i + m] != -1)
			printf("%d ",i);
	}
	puts("");
	for(int i=1; i<=m; i++){
		if(dis[i] != -1)
			printf("%d ",i);
	}
	puts("");
	printf("%d\n",ans);
	return 0;
}

分配问题

题目分析：

这其实就是二分图的最优匹配，可以考虑使用费用流来解决。
考虑分成两个点集工人、工作。
工人向工作连边，流量为 \(1\) 费用为收益；源点向工人连边，流量为 \(1\) 费用为 \(0\)；工作向汇点连边，流量为 \(1\) 费用为 \(0\)。
最后求一边最大费用最大流就是答案。

正确性可以参考二分图最大匹配，也相当显然。

代码：

点击查看代码 
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
const int M = 2e6+5;
const int INF = 1e9+5;
struct edge{
	int nxt,to,val,cost;
	edge(){}
	edge(int _nxt,int _to,int _val,int _cost){
		nxt = _nxt,to = _to,val = _val,cost = _cost;
	}
}e[M];
int cnt=1,S,T,head[N],cur[N],dis[N];
bool vis[N],in_que[N];
void add_edge(int from,int to,int val,int cost){
	e[++cnt] = edge(head[from],to,val,cost);
	head[from] = cnt;
	e[++cnt] = edge(head[to],from,0,-cost);
	head[to] = cnt;
}
bool spfa(int opt){
	if(opt)	memset(dis,0x3f,sizeof(dis));
	else	memset(dis,-0x3f,sizeof(dis));
	memset(vis,false,sizeof(vis));memcpy(cur,head,sizeof(head));
	queue<int> q;q.push(S);dis[S] = 0;in_que[S] = true;
	while(!q.empty()){
		int now = q.front();q.pop();in_que[now] = false;
		for(int i = head[now]; i; i = e[i].nxt){
			int to = e[i].to;
			if(opt){
				if(dis[to] > dis[now] + e[i].cost && e[i].val){
					dis[to] = dis[now] + e[i].cost;
					if(!in_que[to]){
						q.push(to);
						in_que[to] = true;
					}
				}
			}
			else{
				if(dis[to] < dis[now] + e[i].cost && e[i].val){
					dis[to] = dis[now] + e[i].cost;
					if(!in_que[to]){
						q.push(to);
						in_que[to] = true;
					}
				}
			}
		}
	}
	return abs(dis[T]) < 100000000;
}
int dfs(int now,int limit){
	if(now == T)	return limit;
	int flow = 0;vis[now] = true;
	for(int i = cur[now];i && flow < limit;i = e[i].nxt){
		cur[now] = i;
		int to = e[i].to;
		if(dis[to] == dis[now] + e[i].cost && e[i].val && !vis[to]){
			int h = dfs(to,min(limit-flow,e[i].val));
			if(!h)	dis[h] = -1;
			e[i].val -= h;e[i^1].val += h;flow += h;
		}
	}
	return flow;
}
void dinic(){
	int ans = 0,flow;
	while(spfa(1)){
		while(flow = dfs(S,INF)){
			ans += flow * dis[T];
		}
	}
	printf("%d\n",ans);
	for(int i=2; i<=cnt; i+=2){
		e[i].val += e[i^1].val;
		e[i^1].val = 0;
	}
	ans = 0;
	while(spfa(0)){
		while(flow = dfs(S,INF)){
			ans += flow * dis[T];
		}
	}
	printf("%d\n",ans);
}
int main(){
//	freopen("in.txt","r",stdin);
//	freopen("out.txt","w",stdout);
	int n;
	scanf("%d",&n);
	S = n * n + 1,T = S + 1;
	for(int i=1; i<=n; i++){
		add_edge(S,i,1,0);
		add_edge(i+n,T,1,0);
		for(int j=1; j<=n; j++){
			int v;scanf("%d",&v);
			add_edge(i,j+n,1,v);
		}
	}
	dinic();
	return 0;
}

方格取数问题

题目分析：

显然可以转化为最大权独立集问题。
而且可以发现一个性质我们如果将 \(x + y\) 为偶数的点称为黑点，将 \(x + y\) 为奇数的点称为白点，那么我们的边都是在黑点与白点之间的，所以也就是一个二分图问题。

一个结论：最大权独立集 = 总点权和 - 最小权点覆盖
对于最小权点覆盖问题：
源点向一个点集连边，流量为贡献的大小；汇点向另一个点集连边，流量为贡献的大小；两个点集原有的边保留，流量为 \(+\infty\)。
我们最后的最大可行流的大小就是答案。

代码：

点击查看代码 
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
const int M = 2e6+5;
const int INF = 1e9+5;
struct edge{
	int nxt,to,val;
	edge(){}
	edge(int _nxt,int _to,int _val){
		nxt = _nxt,to = _to,val = _val;
	}
}e[M];
int cnt = 1,n,m,S,T,head[N],cur[N],dis[N];
void add_edge(int from,int to,int val){
	e[++cnt] = edge(head[from],to,val);
	head[from] = cnt;
	e[++cnt] = edge(head[to],from,0);
	head[to] = cnt; 
}
bool bfs(){
	memset(dis,-1,sizeof(dis));memcpy(cur,head,sizeof(head));
	queue<int> q;q.push(S);dis[S] = 1;
	while(!q.empty()){
		int now = q.front();q.pop();
		for(int i = head[now]; i; i = e[i].nxt){
			int to = e[i].to;
			if(dis[to] == -1 && e[i].val){
				dis[to] = dis[now] + 1;
				q.push(to);
			}
		}
	}
	return dis[T] != -1;
}
int dfs(int now,int limit){
	if(now == T)	return limit;
	int flow = 0;
	for(int i = cur[now]; i && flow < limit; i = e[i].nxt){
		cur[now] = i;
		int to = e[i].to;
		if(dis[to] == dis[now] + 1 && e[i].val){
			int h = dfs(to,min(limit - flow,e[i].val));
			e[i].val -= h;e[i^1].val += h;flow += h;
			if(!h)	dis[to] = -1;
		}
	}
	return flow;
}
int dinic(){
	int ans = 0,flow;
	while(bfs()){
		while(flow = dfs(S,INF)){
			ans += flow;
		}
	}
	return ans;
}
int num(int i,int j){
	return (i-1) * m + j;
}
int main(){
//	freopen("in.txt","r",stdin);
//	freopen("out.txt","w",stdout);
	scanf("%d%d",&n,&m);
	S = n * m + 1,T = S + 1;
	int sum = 0;
	for(int i=1; i<=n; i++){
		for(int j=1; j<=m; j++){
			int v;scanf("%d",&v);
			if((i + j) & 1)	add_edge(S,num(i,j),v);
			else	add_edge(num(i,j),T,v);
			sum += v;
		}
	}
	for(int i=1; i<=n; i++){
		for(int j=1; j<=m; j++){
			if(i != n){
				if((i + j) & 1)	add_edge(num(i,j),num(i+1,j),INF);
				else	add_edge(num(i+1,j),num(i,j),INF);
			}
			if(j != m){
				if((i + j) & 1)	add_edge(num(i,j),num(i,j+1),INF);
				else	add_edge(num(i,j+1),num(i,j),INF);
			}
		}
	}
	printf("%d\n",sum - dinic());
	return 0;
}

运输问题

题目分析：

我们可以考虑使用费用流模型建边。
源点向仓库连边，流量为容量，费用为 \(0\)；仓库向零售商店连边，流量为 \(+\infty\)，费用为花费的大小；零售商店向汇点连边，流量为容量，费用为 \(0\)。
最后求一遍最小费用最大流就是答案。

代码：

点击查看代码 
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
const int M = 2e6+5;
const int INF = 1e9+5;
struct edge{
	int nxt,to,val,cost;
	edge(){}
	edge(int _nxt,int _to,int _val,int _cost){
		nxt = _nxt,to = _to,val = _val,cost = _cost;
	}
}e[M];
int cnt=1,S,T,head[N],cur[N],dis[N];
bool vis[N],in_que[N];
void add_edge(int from,int to,int val,int cost){
	e[++cnt] = edge(head[from],to,val,cost);
	head[from] = cnt;
	e[++cnt] = edge(head[to],from,0,-cost);
	head[to] = cnt;
}
bool spfa(int opt){
	if(opt)	memset(dis,0x3f,sizeof(dis));
	else	memset(dis,-0x3f,sizeof(dis));
	memset(vis,false,sizeof(vis));memcpy(cur,head,sizeof(head));
	queue<int> q;q.push(S);dis[S] = 0;in_que[S] = true;
	while(!q.empty()){
		int now = q.front();q.pop();in_que[now] = false;
		for(int i = head[now]; i; i = e[i].nxt){
			int to = e[i].to;
			if(opt){
				if(dis[to] > dis[now] + e[i].cost && e[i].val){
					dis[to] = dis[now] + e[i].cost;
					if(!in_que[to]){
						q.push(to);
						in_que[to] = true;
					}
				}
			}
			else{
				if(dis[to] < dis[now] + e[i].cost && e[i].val){
					dis[to] = dis[now] + e[i].cost;
					if(!in_que[to]){
						q.push(to);
						in_que[to] = true;
					}
				}
			}
		}
	}
	return abs(dis[T]) < 100000000;
}
int dfs(int now,int limit){
	if(now == T)	return limit;
	int flow = 0;vis[now] = true;
	for(int i = cur[now];i && flow < limit;i = e[i].nxt){
		cur[now] = i;
		int to = e[i].to;
		if(dis[to] == dis[now] + e[i].cost && e[i].val && !vis[to]){
			int h = dfs(to,min(limit-flow,e[i].val));
			if(!h)	dis[h] = -1;
			e[i].val -= h;e[i^1].val += h;flow += h;
		}
	}
	return flow;
}
void dinic(){
	int ans = 0,flow;
	while(spfa(1)){
		while(flow = dfs(S,INF)){
			ans += flow * dis[T];
		}
	}
	printf("%d\n",ans);
	for(int i=2; i<=cnt; i+=2){
		e[i].val += e[i^1].val;
		e[i^1].val = 0;
	}
	ans = 0;
	while(spfa(0)){
		while(flow = dfs(S,INF)){
			ans += flow * dis[T];
		}
	}
	printf("%d\n",ans);
}
int main(){
//	freopen("in.txt","r",stdin);
//	freopen("out.txt","w",stdout);
	int n,m;
	scanf("%d%d",&n,&m);
	S = n + m + 1,T = S + 1;
	for(int i=1; i<=n; i++){
		int a;scanf("%d",&a);
		add_edge(S,i,a,0);
	}
	for(int i=1; i<=m; i++){
		int b;scanf("%d",&b);
		add_edge(i+n,T,b,0);
	}
	for(int i=1; i<=n; i++){
		for(int j=1; j<=m; j++){
			int v;scanf("%d",&v);
			add_edge(i,j+n,INF,v);
		}
	}
	dinic();
	return 0;
}

餐巾计划问题

题目分析：

可以使用费用流模型来解决这个问题。

我们可以考虑将毛巾拆点分为旧毛巾和新毛巾分别考虑。
考虑旧毛巾的来源：

  • 今天用完的毛巾，所以从源点连向这个点流量为 \(r_i\)，费用为 \(0\)
  • 上一天的旧毛巾，所以从上一天的旧毛巾连向当前点，流量为 \(+\infty\)，费用为 \(0\)

考虑新毛巾的来源：

  • 直接买的毛巾，所以从源点向这个点连边流量为 \(+\infty\)，费用为花费
  • 从慢洗部洗来，那么就从对应时间的旧毛巾连向当前点，流量为 \(+\infty\)，费用为花费
  • 从快洗部洗来，那么就从对应时间的旧毛巾连向当前点，流量为 \(+\infty\)，费用为花费

我们还需要考虑使用毛巾，那么也就是从新毛巾的点连向汇点，流量为 \(r_i\)，费用为 \(0\)。

然后跑一边最小费用最大流，如果最后流量可以使得汇点满流即有解，最优解就是我们求出来的值。

代码：

点击查看代码 
#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e5+5;
const int M = 2e6+5;
const int INF = 1e13+5;
struct edge{
	int nxt,to,val,cost;
	edge(){}
	edge(int _nxt,int _to,int _val,int _cost){
		nxt = _nxt,to = _to,val = _val,cost = _cost;
	}
}e[M];
int cnt=1,S,T,cur[N],head[N],dis[N],r[N];
bool vis[N],in_que[N];
void add_edge(int from,int to,int val,int cost){
	e[++cnt] = edge(head[from],to,val,cost);
	head[from] = cnt;
	e[++cnt] = edge(head[to],from,0,-cost);
	head[to] = cnt;
}
bool spfa(){
	memset(dis,0x3f,sizeof(dis));memset(vis,false,sizeof(vis));memcpy(cur,head,sizeof(head));
	queue<int> q;q.push(S);dis[S] = 0;in_que[S] = true;
	while(!q.empty()){
		int now = q.front();q.pop();in_que[now] = false;
		for(int i = head[now]; i;i = e[i].nxt){
			int to = e[i].to;
			if(dis[to] > dis[now] + e[i].cost && e[i].val){
				dis[to] = dis[now] + e[i].cost;
				if(!in_que[to]){
					q.push(to);
					in_que[to] = true;
				}
			}
		}
	}
	return dis[T] < 100000000;
}
int dfs(int now,int limit){
	if(now == T)	return limit;
	int flow = 0;vis[now] = true;
	for(int i = cur[now]; i && flow < limit; i = e[i].nxt){
		cur[now] = i;
		int to = e[i].to;
		if(dis[to] == dis[now] + e[i].cost && e[i].val && !vis[to]){
			int h = dfs(to,min(limit-flow,e[i].val));
			e[i].val -= h;e[i^1].val += h;flow += h;
		}
	}
	return flow;
}
int dinic(){
	int ans = 0,flow;
	while(spfa()){
		while(flow = dfs(S,INF)){
			ans += flow * dis[T];
		}
	}
	return ans;
}
signed main(){
//	freopen("in.txt","r",stdin);
//	freopen("out.txt","w",stdout);
	int n;
	scanf("%lld",&n);
	S = n * 2 + 1,T = S + 1;
	for(int i=1; i<=n; i++){
		scanf("%lld",&r[i]);
	}
	int a,b,c,d,e;
	scanf("%lld%lld%lld%lld%lld",&a,&b,&c,&d,&e);
	for(int i=1; i<=n; i++){
		//考虑新毛巾的来源 
		add_edge(S,i+n,INF,a);
		if(i > b)	add_edge(i-b,i+n,INF,c);
		if(i > d)	add_edge(i-d,i+n,INF,e);
		//考虑旧毛巾的来源 
		add_edge(S,i,r[i],0);
		if(i > 1)	add_edge(i-1,i,INF,0);
		//使用毛巾 
		add_edge(i+n,T,r[i],0);
	}
	printf("%lld\n",dinic());
	return 0;
}

骑士共存问题

题目分析：

显然是最大权独立集问题。

我们将每个点向从这个点的骑士能到达的且有用的点连边，这个问题里可以将权值理解为 \(1\)。
我们发现可以按 \(x + y\) 的奇偶分类，也就是可以转化为二分图的问题，也就可以做了。

结论：最大权独立集 = 总权值和 - 最小权点覆盖

注意这里的总权值和是去掉不可用的点之后的。

代码：

点击查看代码 
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
const int M = 2e6+5;
const int INF = 1e9+5;
struct edge{
	int nxt,to,val;
	edge(){}
	edge(int _nxt,int _to,int _val){
		nxt = _nxt,to = _to,val = _val;
	}
}e[M];
int cnt=1,S,T,n,m,head[N],dis[N],cur[N];
int dx[] = {0,1,1,-1,-1,2,2,-2,-2};
int dy[] = {0,2,-2,2,-2,1,-1,1,-1};
bool vis[1000][1000];
void add_edge(int from,int to,int val){
	e[++cnt] = edge(head[from],to,val);
	head[from] = cnt;
	e[++cnt] = edge(head[to],from,0);
	head[to] = cnt;
}
bool bfs(){
	memset(dis,-1,sizeof(dis));memcpy(cur,head,sizeof(head));
	queue<int> q;q.push(S);dis[S] = 1;
	while(!q.empty()){
		int now = q.front();q.pop();
		for(int i = head[now]; i; i = e[i].nxt){
			int to = e[i].to;
			if(dis[to] == - 1 && e[i].val){
				dis[to] = dis[now] + 1;
				q.push(to);
			}
		}
	}
	return dis[T] != -1;
}
int dfs(int now,int limit){
	if(now == T)	return limit;
	int flow = 0;
	for(int i = cur[now]; i && flow < limit; i = e[i].nxt){
		cur[now] = i;
		int to = e[i].to;
		if(dis[to] == dis[now] + 1 && e[i].val){
			int h = dfs(to,min(limit - flow,e[i].val));
			e[i].val -= h;e[i^1].val += h;flow += h;
			if(!h)	dis[to] = -1;
		}
	}
	return flow;
}
int dinic(){
	int ans = 0,flow;
	while(bfs()){
		while(flow = dfs(S,INF)){
			ans += flow;
		}
	}
	return ans;
}
int num(int i,int j){
	return (i-1)*n + j;
}
int main(){
//	freopen("in.txt","r",stdin);
//	freopen("out.txt","w",stdout);
	scanf("%d%d",&n,&m);
	S = n * n + 1,T = S + 1;
	for(int i=1; i<=m; i++){
		int x,y;scanf("%d%d",&x,&y);
		vis[x][y] = true;
	}
	int sum = 0;
	for(int i=1; i<=n; i++){
		for(int j=1; j<=n; j++){
			if(vis[i][j])	continue;
			if((i + j) & 1)	add_edge(S,num(i,j),1);
			else	add_edge(num(i,j),T,1);
			for(int k=1; k<=8; k++){
				int x = i + dx[k];
				int y = j + dy[k];
				if(x >= 1 && x <= n && y >= 1 && y <= n && !vis[x][y]){
					if((i + j) & 1)	add_edge(num(i,j),num(x,y),INF);
					else	add_edge(num(x,y),num(i,j),INF);
//					printf("(%d,%d) (%d,%d) INF\n",i,j,x,y);
				}
			}
			++sum;
		}
	}
	printf("%d\n",sum - dinic());
	return 0;
}

数字梯形问题

题目分析：

显然可以使用费用流模型求解。

对于第一问：
因为我们需要限制每个点最多走一次所以拆点，流量为 \(1\)，费用为点权。因为我们需要限制每一条边最多走一次，所以边的流量为 \(1\)，费用为 \(0\)。
那么显然的建图：从源点向最顶部的点连边，流量为 \(1\)，费用为 \(0\)。从每个点向它可以到达的点连边，流量为 \(1\)，费用为 \(0\)。从最底层的点向汇点连边，流量为 \(1\)，费用为 \(0\)。
那么求一次最大费用最大流就是答案。

对于第二问：
就是将对于点的限制解开了，那么我们就将点内部的边的流量改为 \(+\infty\) 就好了。

对于第三问：
就是将对于边的限制解开了，那么就将各个边的流量设为 \(+\infty\) 就好了。注意这里不能将源点连向最顶层的点的流量设为 \(+\infty\)，因为是从这些数开始，不可能从某一个数开始多次。我们向汇点的边需要设为 \(+\infty\)，因为这样保证了最后的点可以走多次。

代码：

点击查看代码 
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
const int M = 2e6+5;
const int INF = 1e9+5;
struct edge{
	int nxt,to,val,cost;
	edge(){}
	edge(int _nxt,int _to,int _val,int _cost){
		nxt = _nxt,to = _to,val = _val,cost = _cost;
	}
}e[M];
int n,m,tot,S,T,cnt=1,dis[N],cur[N],head[N],id[50][50],v[50][50];
bool vis[N],in_que[N];
void add_edge(int from,int to,int val,int cost){
	e[++cnt] = edge(head[from],to,val,cost);
	head[from] = cnt;
	e[++cnt] = edge(head[to],from,0,-cost);
	head[to] = cnt;
}
bool spfa(){
	memset(dis,-0x3f,sizeof(dis));memcpy(cur,head,sizeof(head));
	memset(vis,false,sizeof(vis));
	queue<int> q;q.push(S);dis[S] = 0;in_que[S] = true;
	while(!q.empty()){
		int now = q.front();q.pop();in_que[now] = false;
		for(int i = head[now]; i; i = e[i].nxt){
			int to = e[i].to;
			if(dis[to] < dis[now] + e[i].cost && e[i].val){
				dis[to] = dis[now] + e[i].cost;
				if(!in_que[to]){
					q.push(to);
					in_que[to] = true;
				}
			}
		}
	}
	return abs(dis[T]) < 100000000;
}
int dfs(int now,int limit){
	if(now == T)	return limit;
	int flow = 0;vis[now] = true;
	for(int i = cur[now]; i && flow < limit; i = e[i].nxt){
		cur[now] = i;
		int to = e[i].to;
		if(dis[to] == dis[now] + e[i].cost && e[i].val && !vis[to]){
			int h = dfs(to,min(limit-flow,e[i].val));
			e[i].val -= h;e[i^1].val += h;flow += h;
			if(!h)	dis[to] = -1;
		}
	}
	return flow;
}
int dinic(){
	int ans = 0,flow;
	while(spfa())
		while(flow = dfs(S,INF))
			ans += flow * dis[T];
	return ans;
}
int main(){
//	freopen("in.txt","r",stdin);
//	freopen("out.txt","w",stdout);
	scanf("%d%d",&m,&n);
	S = ++tot,T = ++tot;
	for(int i=1; i<=n; i++){
		for(int j=1; j<=m+i-1; j++){
			id[i][j] = ++tot;
			scanf("%d",&v[i][j]);
		}
	}
	//规则1
	memset(head,0,sizeof(head));cnt = 1;
	for(int i=1; i<=n; i++){
		for(int j=1; j<=m+i-1; j++){
			add_edge(id[i][j],id[i][j]+tot,1,v[i][j]);
			if(i < n){
				add_edge(id[i][j]+tot,id[i+1][j],1,0);
				add_edge(id[i][j]+tot,id[i+1][j+1],1,0);
			}
			if(i == 1)	add_edge(S,id[i][j],1,0);
			if(i == n)	add_edge(id[i][j]+tot,T,1,0);
		}
	} 
	printf("%d\n",dinic());
	
	//规则2 
	memset(head,0,sizeof(head));cnt = 1;
	for(int i=1; i<=n; i++){
		for(int j=1; j<=m+i-1; j++){
			add_edge(id[i][j],id[i][j]+tot,INF,v[i][j]);
			if(i < n){
				add_edge(id[i][j]+tot,id[i+1][j],1,0);
				add_edge(id[i][j]+tot,id[i+1][j+1],1,0);
			}
			if(i == 1)	add_edge(S,id[i][j],1,0);  //只有 m 条路径，所以必须流量为 1 
			if(i == n)	add_edge(id[i][j]+tot,T,INF,0);  //可以从任意一个点结束，所以任意一个点的流量无限制 
		}
	} 
	printf("%d\n",dinic());
	
	//规则 3
	 memset(head,0,sizeof(head));cnt = 1;
	for(int i=1; i<=n; i++){
		for(int j=1; j<=m+i-1; j++){
			add_edge(id[i][j],id[i][j]+tot,INF,v[i][j]);
			if(i < n){
				add_edge(id[i][j]+tot,id[i+1][j],INF,0);
				add_edge(id[i][j]+tot,id[i+1][j+1],INF,0);
			}
			if(i == 1)	add_edge(S,id[i][j],1,0);
			if(i == n)	add_edge(id[i][j]+tot,T,INF,0);
		}
	} 
	printf("%d\n",dinic());
	return 0;
}

负载平衡问题

题目分析：

可以考虑使用费用流模型。
我们显然有用的流量就是从有多余库存的点流向库存不够的点。
那么我们就考虑从源点向多余库存的点连边，流量为多余的库存，费用为 \(0\)；从库存呢不够的点向汇点连边，流量为不够的库存；相邻的仓库之间建边，流量为 \(+\infty\)，费用为 \(1\)。
那么跑一边最小费用最大流就是答案。

代码：

点击查看代码 
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
const int M = 2e6+5;
const int INF = 1e9+5;
struct edge{
	int nxt,to,val,cost;
	edge(){}
	edge(int _nxt,int _to,int _val,int _cost){
		nxt = _nxt,to = _to,val = _val,cost = _cost;
	}
}e[M];
int cnt=1,S,T,head[N],cur[N],dis[N],v[N];
bool vis[N],in_que[N];
void add_edge(int from,int to,int val,int cost){
	e[++cnt] = edge(head[from],to,val,cost);
	head[from] = cnt;
	e[++cnt] = edge(head[to],from,0,-cost);
	head[to] = cnt;
}
bool spfa(){
	memset(dis,0x3f,sizeof(dis));memcpy(cur,head,sizeof(head));
	memset(vis,false,sizeof(vis));
	queue<int> q;q.push(S);dis[S] = 0;in_que[S] = true;
	while(!q.empty()){
		int now = q.front();q.pop();in_que[now] = false;
		for(int i = head[now]; i;i = e[i].nxt){
			int to = e[i].to;
			if(dis[to] > dis[now] + e[i].cost && e[i].val){
				dis[to] = dis[now] + e[i].cost;
				if(!in_que[to]){
					q.push(to);
					in_que[to] = true;
				}
			}
		}
	}
	return dis[T] < 100000000;
}
int dfs(int now,int limit){
	if(now == T)	return limit;
	int flow = 0;vis[now] = true;
	for(int i = cur[now]; i && flow < limit; i = e[i].nxt){
		cur[now] = i;
		int to = e[i].to;
		if(dis[to] == dis[now] + e[i].cost && e[i].val && !vis[to]){
			int h = dfs(to,min(limit-flow,e[i].val));
			e[i].val -= h;e[i^1].val += h;flow += h;
			if(!h)	dis[to] = -1;
		}
	}
	return flow;
}
int dinic(){
	int ans = 0,flow;
	while(spfa()){
		while(flow = dfs(S,INF)){
			ans += flow * dis[T];
		}
	}
	return ans;
}
int main(){
//	freopen("in.txt","r",stdin);
//	freopen("out.txt","w",stdout);
	int n;
	scanf("%d",&n);
	S = n + 1,T = S + 1;
	int sum = 0;
	for(int i=1; i<=n; i++){
		scanf("%d",&v[i]);
		sum += v[i];
	}
	sum /= n;
	for(int i=1; i<=n; i++){
		if(v[i] > sum)	add_edge(S,i,v[i]-sum,0);
		else	if(v[i] < sum)	add_edge(i,T,sum-v[i],0);
		if(i != 1)	add_edge(i,i-1,INF,1);
		else	add_edge(i,n,INF,1);
		if(i != n)	add_edge(i,i+1,INF,1);
		else	add_edge(n,1,INF,1);
	}
	printf("%d\n",dinic());
	return 0;
}

深海机器人问题

题目分析：

可以使用费用流模型。
因为权值在边上所以并不需要拆点。
因为每个边的贡献只可以被算一次，所以可以考虑在两个点之间建两种边：

  1. 容量为 \(1\)，费用为该边的贡献
  2. 容量为 \(+\infty\)，费用为 \(0\)

这样最大费用最大流即答案。

代码：

点击查看代码 
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
const int M = 2e6+5;
const int INF = 1e9+5;
struct edge{
	int nxt,to,val,cost;
	edge(){}
	edge(int _nxt,int _to,int _val,int _cost){
		nxt = _nxt,to = _to,val = _val,cost = _cost;
	}
}e[M];
int cnt=1,S,T,p,q,cur[N],head[N],dis[N];
bool vis[N],in_que[N];
void add_edge(int from,int to,int val,int cost){
	e[++cnt] = edge(head[from],to,val,cost);
	head[from] = cnt;
	e[++cnt] = edge(head[to],from,0,-cost);
	head[to] = cnt;
}
bool spfa(){
	memset(dis,-0x3f,sizeof(dis));memset(vis,false,sizeof(vis));memcpy(cur,head,sizeof(head));
	queue<int> q;q.push(S);dis[S] = 0;in_que[S] = true;
	while(!q.empty()){
		int now = q.front();q.pop();in_que[now] = false;
		for(int i = head[now]; i;i = e[i].nxt){
			int to = e[i].to;
			if(dis[to] < dis[now] + e[i].cost && e[i].val){
				dis[to] = dis[now] + e[i].cost;
				if(!in_que[to]){
					q.push(to);
					in_que[to] = true;
				}
			}
		}
	}
	return dis[T] > -100000000;
}
int dfs(int now,int limit){
	if(now == T)	return limit;
	int flow = 0;vis[now] = true;
	for(int i = cur[now]; i && flow < limit;i = e[i].nxt){
		cur[now] = i;
		int to = e[i].to;
		if(dis[to] == dis[now] + e[i].cost && e[i].val && !vis[to]){
			int h = dfs(to,min(limit-flow,e[i].val));
			e[i].val -= h;e[i^1].val += h;flow += h;
			if(!h)	dis[to] = -1;
		}
	}
	return flow;
}
int dinic(){
	int ans = 0,flow;
	while(spfa()){
		while(flow = dfs(S,INF)){
			ans += flow * dis[T];
		}
	}
	return ans;
}
int id(int i,int j){
	return (i-1) * q + j;
}
int main(){
//	freopen("in.txt","r",stdin);
//	freopen("out.txt","w",stdout);
	int a,b;
	scanf("%d%d",&a,&b);
	scanf("%d%d",&p,&q);
	p++;q++;
	S = p * q + 1,T = S + 1;
	for(int i=1; i<=p; i++){
		for(int j=1; j<q; j++){
			int v;scanf("%d",&v);
			//从(i,j) 到 (i,j+1)
			add_edge(id(i,j),id(i,j+1),1,v);
			add_edge(id(i,j),id(i,j+1),INF,0);
//			printf("(%d,%d) (%d,%d)\n",i,j,i,j+1);
		}
	}
	for(int i=1; i<=q; i++){
		for(int j=1; j<p; j++){
			int v;scanf("%d",&v);
			add_edge(id(j,i),id(j+1,i),1,v);
			add_edge(id(j,i),id(j+1,i),INF,0);
//			printf("(%d,%d) (%d,%d)\n",j,i,j+1,i);
		}
	}
	for(int i=1; i<=a; i++){
		int k,x,y;
		scanf("%d%d%d",&k,&x,&y);x++;y++;
		add_edge(S,id(x,y),k,0);
//		printf("S (%d,%d)\n",x,y);
	}
	for(int i=1; i<=b; i++){
		int k,x,y;
		scanf("%d%d%d",&k,&x,&y);x++;y++;
		add_edge(id(x,y),T,k,0);
//		printf("(%d,%d) T\n",x,y);
	}
	printf("%d\n",dinic());
	return 0;
}

最长不下降子序列问题

题目分析：

考虑对于第一问，我们显然可以通过 \(DP\) 求解，即设 \(dp[i]\) 表示以 \(i\) 个点为结尾的最长的不降子序列的长度。
这样转移就显然是：

\[dp[i] = \max_{j < i \and x[j] \le x[i]} dp[j] + 1 \]

对于第二问，我们考虑网络流的建模：
对于 \(i\)，将满足 \(dp[j] + 1 = dp[i]\) 的 \(j\) 与 \(i\) 连边，因为每个点只能选择一次，所以流量为 \(1\)。
但是我们发现这样仍然无法限制住每个点只能选一次的条件，所以考虑拆点，将两个点之间连接边流量 \(1\)。

我们设第一问的答案为 \(s\)。
则将满足 \(dp[i] = 1\) 的 \(i\) 与 \(S\) 连边，将满足 \(dp[i] = s\) 的 \(i\) 与 \(T\) 连边，流量均为 \(1\)。
可以发现，我们的每一点流量一定是对应着一条不同的长度为 \(s\) 的不降子序列，所以跑一遍最大流就好了。
对于第三问，我们发现就是去掉了对 \(1\) 和 \(n\) 的限制，所以他们的流量限制放开就好了。

注意：如果 \(n\) 与 \(T\) 之间没有边，那么不能强行加边，如果有边才能设为 \(+\infty\)，此处就需要好好理解题意，就能明白了。

代码：

点击查看代码 
#include<bits/stdc++.h>
using namespace std;
const int N = 1e5+5;
const int M = 2e6+5;
const int INF = 1e9+5;
struct edge{
	int nxt,to,val;
	edge(){}
	edge(int _nxt,int _to,int _val){
		nxt = _nxt,to = _to,val = _val;
	}
}e[M];
int cnt = 1,S,T,head[N],dis[N],a[N],cur[N],f[N];
void add(int from,int to,int val){
	e[++cnt] = edge(head[from],to,val);
	head[from] = cnt;
	e[++cnt] = edge(head[to],from,0);
	head[to] = cnt;
}
bool bfs(){
	memset(dis,-1,sizeof(dis));memcpy(cur,head,sizeof(head));
	queue<int> q;
	q.push(S);dis[S] = 1;
	while(!q.empty()){
		int now = q.front();q.pop();
		for(int i = head[now]; i; i =e[i].nxt){
			int to = e[i].to;
			if(e[i].val && dis[to] == -1){
				dis[to] = dis[now] + 1;
				q.push(to);
			}
		}
	} 
	return dis[T] != -1;
}
int dfs(int now,int limit){
	if(now == T)	return limit;
	int flow = 0;
	for(int i = cur[now]; i && flow < limit; i = e[i].nxt){
		cur[now] = i;
		int to = e[i].to;
		if(dis[to] == dis[now] + 1 && e[i].val){
			int h = dfs(to,min(limit - flow,e[i].val));
			if(!h)	dis[to] = INF;
			e[i].val -= h;e[i^1].val += h;flow += h;
		}
	}
	return flow;
}
int dinic(){
	int ans = 0,flow;
	while(bfs()){
		while(flow = dfs(S,INF)){
			ans += flow;
		}
	}
	return ans;
}
int main(){
//	freopen("in.txt","r",stdin);
//	freopen("out.txt","w",stdout);
	int n;
	scanf("%d",&n);
	S = n + n + 1,T = S + 1;
	for(int i=1; i<=n; i++){
		scanf("%d",&a[i]);
	}
	int s = -INF;
	for(int i=1; i<=n; i++){
		add(i,i+n,1);f[i] = 1;
		for(int j=1; j<i; j++){
			if(a[j] <= a[i])
				f[i] = max(f[i],f[j] + 1);
		}
		for(int j=1; j<i; j++){
			if(a[j] <= a[i] && f[i] == f[j] + 1){
				add(j+n,i,1);
			}
		}
		s = max(s,f[i]);
	}
	for(int i=1; i<=n; i++){
		if(f[i] == 1)	add(S,i,1);
		else if(f[i] == s)	add(i+n,T,1);
	}
	printf("%d\n",s);
	if(s == 1){  //一会看看需不需要特判 
		printf("%d\n%d\n",n,n); 
		return 0;
	}
	int ans = dinic();
	printf("%d\n",ans);
	for(int i=2; i<=cnt; i++){
		int from = e[i^1].to,to = e[i].to;
		if(from == S && to == 1)	e[i].val = INF;  //容量 -> INF 然后增广 
		if(from == 1 && to == 1 + n)	e[i].val = INF;
		if(from == n && to == n + n)	e[i].val = INF;
		if(from == n + n && to == T)	e[i].val = INF;
	}
	ans = ans + dinic();
	printf("%d\n",ans);
	return 0;
}

最小路径覆盖问题

题目分析：

（路径覆盖指的是DAG 顶点覆盖）
我们认为一开始 DAG 被 \(n\) 条路径覆盖，也就是每条路径只包含一个点。
我们考虑每一次合并两个路径，也就是下面这种做法。
拆点，一个点 \(i\) 拆为 \((x_i,y_i)\)，连边 \((S,x_i)(y_i,T)\)，对于原图中的一条边 \((a,b)\) 则连边 \((x_a,y_b)\)。
此时的最大流就是最大的可合并的路径数。

代码：

点击查看代码 
#include<bits/stdc++.h>
const int N = 1e5+5;
const int M = 2e6+5;
const int INF = 1e9+5;
using namespace std;
struct edge{
	int nxt,to,val;
	edge(){}
	edge(int _nxt,int _to,int _val){
		nxt = _nxt,to = _to,val = _val;
	}
}e[M];
int cnt=1,S,T,n,head[N],cur[N],dis[N],nxt[N];
bool flag[N];
void add_edge(int from,int to,int val){
	e[++cnt] = edge(head[from],to,val);
	head[from] = cnt;
	e[++cnt] = edge(head[to],from,0);
	head[to] = cnt;
}
bool bfs(){
	memset(dis,-1,sizeof(dis));memcpy(cur,head,sizeof(head));
	queue<int> q;q.push(S);dis[S] = 1;
	while(!q.empty()){
		int now = q.front();q.pop();
		for(int i = head[now]; i; i = e[i].nxt){
			int to = e[i].to;
			if(dis[to] == -1 && e[i].val){
				dis[to] = dis[now] + 1;
				q.push(to);
			}
		}
	}
	return dis[T] != -1;
}
int dfs(int now,int limit){
	if(now == T)	return limit;
	int flow = 0;
	for(int i = head[now]; i; i = e[i].nxt){
		int to = e[i].to;
		if(dis[to] == dis[now] + 1 && e[i].val){
			int h = dfs(to,min(limit - flow,e[i].val));
			if(h){
				nxt[now] = to;
				if(now != S && to > n)	flag[to-n] = true;
				e[i].val -= h;e[i^1].val += h;flow += h;
			}
			else	dis[to] = -1;
		}
	}
	return flow;
}
int dinic(){
	int ans = 0,flow;
	while(bfs()){
		while(flow = dfs(S,INF)){
			ans += flow;
		}
	}
	return ans;
}
int main(){
//	freopen("in.txt","r",stdin);
//	freopen("out.txt","w",stdout);
	int m;
	scanf("%d%d",&n,&m);
	S = n * 2 + 1,T = S + 1;
	for(int i=1; i<=m; i++){
		int from,to;
		scanf("%d%d",&from,&to);
		add_edge(from,to+n,INF);
//		printf("%d+n %d INF\n",from,to);
	}
	for(int i=1; i<=n; i++){
		add_edge(S,i,1);add_edge(i+n,T,1);
//		printf("S %d 1\n",i);
//		printf("%d+n T 1\n",i);
	}
	int ans = n - dinic();
	for(int i=1; i<=n; i++){
		if(!flag[i]){
			int now = i;
			printf("%d ",i);
			while(nxt[now] != T && nxt[now]){
				printf("%d ",nxt[now] - n);
				now = nxt[now] - n;
			}
			printf("\n");
		}
	}
	printf("%d\n",ans);
	return 0;
}

证明：

最大流最小割定理

相信大家都知道：最大流等于最小割，但是如果不会证明的话对我们解决网络流的题是有很大的阻碍的。
分两个部分来证明：

（一）最大流小于等于最小割
我们考虑任意一个割集 \(c[S,T]\)，因为我们从 \(S\) 到 \(T\) 必定经过割集上的边，所以我们流量的大小不可能超过这个割集的容量的大小，即任意一个可行流的流量小于任意一个割的大小。
由此可以导出：最大流小于等于最小割。
画个图理解一下：

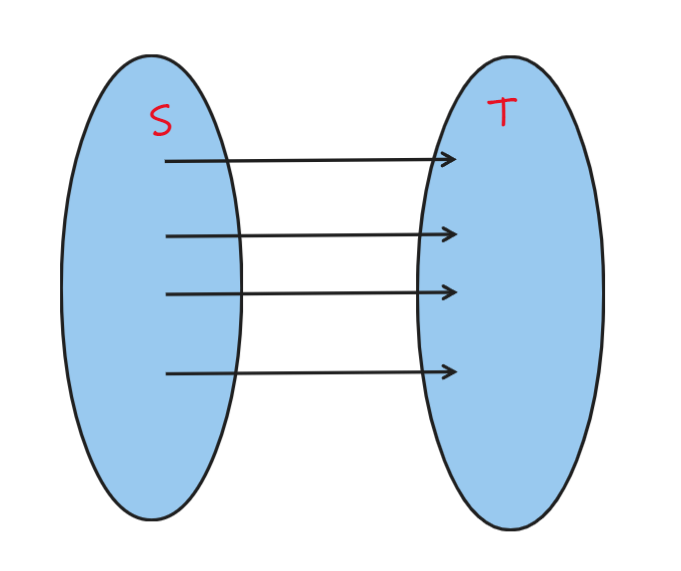
（二）最大流大于等于最小割
考虑一个最大流 \(f\)，在他的残量网络 \(G_f\) 里，在 \(s \to t\) 的每一条路径上，我们都将第一个剩余流量为 \(0\) 的边割掉，显然这些边构成一个割集。
而最大流的大小显然要大于等于这些割边的容量的大小，所以即最大流大于等于这个割的大小，而这个割的大小又大于等于最小割的大小，所以最大流大于等于最小割。
画个图理解一下：

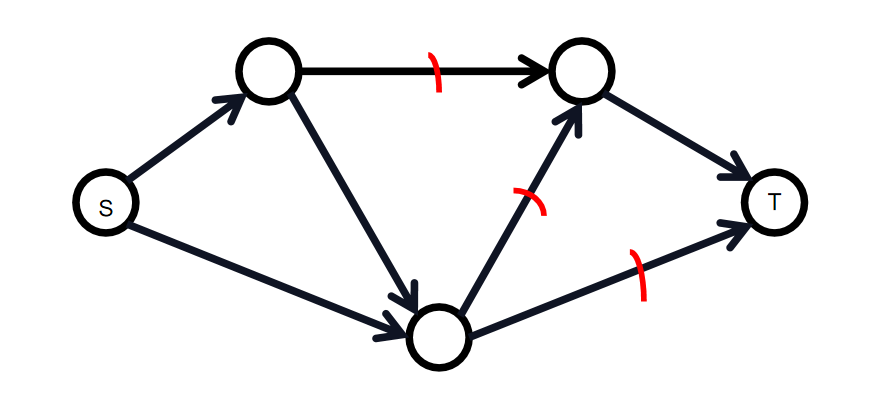
综上：最大流等于最小割

最小点权覆盖集 和 最大权独立集

最小点权覆盖集：

覆盖集：对于一个点集 \(V\)，若对于原图中的每一条边 \((u,v)\) 都存在 \(u \in V\) 或 \(v \in V\)，那么 \(V\) 就是原图的一个覆盖集
最小点权覆盖集：对于所有的覆盖集，点权和最小的覆盖集称为最小点权覆盖集
对于任意图的最小点权覆盖集是 \(NPC\) 问题，但是对于二分图却有一个漂亮的解法。

考虑如下的建边方式：
\(S\) 向其中一个点集连边，流量为该点的权值；点与点之间的边保留，流量为 \(+\infty\)；另一个点集向 \(T\) 连边，流量为该点的权值。
我们的答案即最小割的大小。

若我们定义：割边都是与 \(S\) 或 \(T\) 相连的边的割为简单割。
显然可以发现：最小割一定是一个简单割。

所以我们只需证明每一种覆盖集与一个简单割一一对应即可。

考虑每一个简单割都可以对应一个覆盖集：
我们将割边理解为选择这个点，因为这是一个简单割，所以对于任意一条边 \((u,v)\) 必然存在割掉 \(u\) 或 \(v\) 对应的边，转化到原图上也就是一定会选择 \(u\) 或 \(v\)，也就是一定是一个覆盖集。

考虑每一个覆盖集都可以对应一个简单割：
考虑使用反证法，如果对于某个覆盖集没有办法对应一个简单割，那么就意味着必然存在 \(S \to u \to v \to T\) 的路径，此时 \(u,v\) 都没被割掉，也就是 \((u,v)\) 没有点可以覆盖，与我们的假设是一个覆盖集冲突。

考虑证明简单割与其对应的覆盖集的大小关系：
考虑一个简单割 \(c[S,T]\)，设 \(V_1 = S - \{s\}\)，\(V_2 = V - V_1\)，那么就有 \(c[S,T] = \sum_{u\in V_1} w_{s,u} + \sum_{u \in V_2} w_{u,t}\)
这也就对应着我们选择的点的权值，所以任意一个简单割的大小就等于其对应的覆盖集的大小。
所以对于一个最小点权覆盖集也就是对应着最小割。

最大权独立集：

独立集：对于一个点集 \(V\)，若对于任意 \(u,v \in V\)，都不存在 \((u,v)\) 是原图中的边，那么 \(V\) 就称为一个独立集
最大权独立集：所有的独立集中，点权和最大的独立集称为最大权独立集。

结论：最大权独立集 = 所有点的总权值和 - 最小权点覆盖

下面我们证明：独立集与点覆盖集互为补集。
独立集的补集是点覆盖集：若补集不是一个覆盖集，即存在一条边 \((u,v)\) 使得 \(u,v\) 都未选择，考虑求补集之后，\(u,v\) 都被选择，也就是 \((u,v)\) 这条边的两个端点都被选择，与是独立集的假设冲突。
点覆盖集的补集是独立集：若补集不是一个独立集，即存在一条边 \((u,v)\) 使得 \(u,v\) 都被选择，考虑求补集之后，\(u,v\) 都没有被选择，也就是 \((u,v)\) 这条边的两个端点都没有被选择，与点覆盖集的假设相冲突。

即：独立集 = 总点权和 - 对应的点覆盖集的大小。
那么最大独立集对应的覆盖集也就是最小点覆盖集。
所以结论的证。

最大权闭合子图

基本定义：

闭合子图：给定一个有向图 \(G = (V,E)\)，给定一个点集 \(V'\)，若满足该点集内部的点的所有连边都不会从点集内指向点集外，那么这个点集和点集内部的所有边称为一个闭合子图
最大权闭合子图：所有闭合子图中点权和最大的一个。

求解方法：

最大权闭合子图是最小割模型的一个应用。
我们设原图为 \(G = (V,E)\)，构造出来的流网络为 \(G_N = (V_N,E_N)\)
我们新建一个源点 \(s\)，连向所有权值为正数的点，容量为该点的权值；新建一个汇点 \(t\)，从所有权值为负数的点连向它，容量为该点的权值的绝对值；将原图上的边保留，容量为 \(+\infty\)。
我们最后的答案就是所有权值为正数点的权值和减去这个图的最小割的大小

证明：

我们定义简单割为割边均为与 \(s\) 或 \(t\) 相连的边。
可以证明：最小割一定是一个简单割。
根据最大流最小割定理：最小割等于最大流。因为从源点连出去的边与连向汇点的边的容量有限制，所以最大流有限制，所以也就是最小割有限制，而如果割掉内部的边显然就是最小割没有了限制，所以最小割一定是一个简单割。

我们考虑证明闭合子图与简单割是一一对应的。
我们假定有一个闭合子图 \((V',E')\)，我们构造一个割 \(c[S,T]\)，使得 \(S = V' + \{s\}\) 和 \(T = V_N - S\)。那么就考虑证明这个割是一个简单割。因为 \(V'\) 是一个闭合子图，所以其内部肯定没有连向点集外部的点，所以不可能存在我们割掉各个点之间的连边，所以只可以割掉与 \(s\) 或 \(t\) 相连的边，也就是一定是一个简单割。

考虑证明简单割与闭合子图是一一对应的。
考虑我们有了一个简单割 \(c[S,T]\) 我们构造一个闭合子图 \(G'\)，我们设 \(V_1 = S - \{s\},V_2 = V_N - V_1\)，因为是简单割所以也就是 \(V_1,V_2\) 之间不存在连边，所以从 \(S\) 出发必然回到 \(S\)，所以 \(V_1\) 就是一个闭合点集，也就是 \(G'\) 一定是一个闭合子图。

下面我们就要证明简单割与闭合子图的大小关系。
我们假设有一个简单割 \([S,T]\) 其对应的闭合点集就是 \(V' = S - \{s\}\)，我们规定原图为 \(G = (V,E)\)，设 \(V'' = V - V'\)，我们定义左边的点为 \(V',\{s\}\)，右边的点为 \(V'',\{t\}\)，那么我们可以发现割边一定是左右两边之间的点。而 \(V'\) 与 \(V''\) 之间没有割边，\(\{s\}\) 和 \(\{t\}\) 之间没有割边，所以割边一定是 \(V',\{t\}\) 或 \(V'',\{s\}\)，我们这个割的大小即 \(c[S,T] = \sum c[\{s\},V''] + \sum c[V',\{t\}] = \sum_{u \in V''} w_v + \sum_{u \in V'} -w_u\)
我们定义 \(V^+\) 为 \(V\) 中所有的正权点，\(V^-\) 为所有的负权点。
所以这个割的大小可以写为 \(c[S,T] = \sum_{u \in V''^+} w_u + \sum_{u \in V'^-} (-w_u)\)。
我们同理也可以将闭合子图的权值和写出来 \(w(V') = \sum_{u \in V'^+} w_u - \sum_{u \in V'^-} (-w_u)\)。
可以发现 \(w(V^+) = w(V') + c[S,T]\)，转化一下即：\(w(V') = w(V^+) - c[S,T]\)。
为了使得 \(w(V')\) 最大即让 \(c[S,T]\) 最小，所以所有正权点的点权和减去最小割的大小就是最大权闭合子图的点权和。

posted @ 2022-09-06 14:58  linyihdfj  阅读(59)  评论(0)  编辑  收藏  举报