【学习笔记】CDQ分治（等待填坑）

因为我对CDQ分治理解不深，所以这篇博客只是我现在的浅显理解有任何不对的，希望大佬指出。

---

首先就是CDQ分治适用的题型：
（1）带修改，但修改互相独立
（2）必须允许离线
（3）解决数据结构的题，能把在线的数据结构吊打

---

CDQ分治更多的是一种思想，所以就更加没有模板了，只有一个大体的构造在那里。
下面就说一下CDQ分治的基本思想（我的认为）：
CDQ分治本质上就是按时间分治，即把各个操作按时间排序然后进行处理。

---

其实把这个思想说出来真的不好弄，就看一道经典例题来观察一下什么是CDQ分治

题目描述：

基本思路：

这道题就是CDQ分治的必做题，三维偏序，一句话题解就是：CDQ分治第一维，归并排序第二维，数据结构第三维。即CDQ分治保证第一维有序，在这个前提下对这个序列进行归并排序，这样能保证第二维有序，在归并排序加入的过程中用数据结构存储第三维的信息，这样查找数据结构上的信息也就使得第三维有序。

代码实现：

（不确定这个代码会成为我的最终版代码）



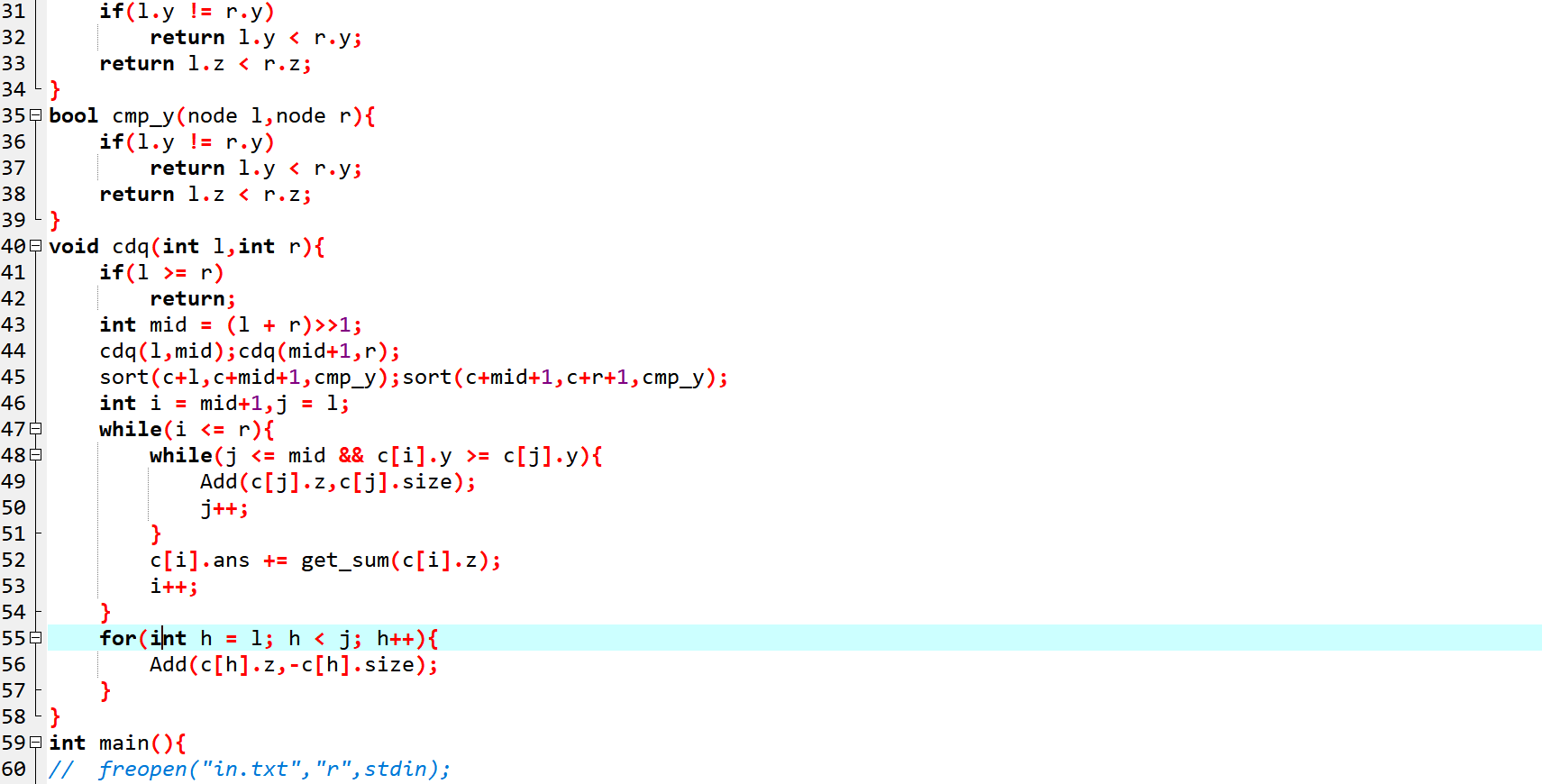
文本版：

#include<bits/stdc++.h>
using namespace std;
const int MAXN = 2e5+5;
struct node{
	int x,y,z,size,ans;
	node(int _x = 0,int _y = 0,int _z = 0,int _size = 1,int _ans = 0){
		x = _x, y = _y,z = _z,size = _size,ans = _ans;
	}
}a[MAXN],c[MAXN];
int cnt,n,k,tree[MAXN],ans[MAXN];
int lowbit(int x){
	return x & (-x);
}
void Add(int x,int y){
	while(x <= k){
		tree[x] += y;
		x += lowbit(x);
	}
}
int get_sum(int x){
	int res = 0;
	while(x){
		res += tree[x];
		x -= lowbit(x);
	}
	return res;
}
bool cmp_x(node l,node r){  //因为我们会进行去重，所以这里应该按顺序一个个全排 
	if(l.x != r.x)
		return l.x < r.x;
	if(l.y != r.y)
		return l.y < r.y;
	return l.z < r.z;
}
bool cmp_y(node l,node r){
	if(l.y != r.y)
		return l.y < r.y;
	return l.z < r.z;
}
void cdq(int l,int r){
	if(l >= r)
		return;
	int mid = (l + r)>>1;
	cdq(l,mid);cdq(mid+1,r);
	sort(c+l,c+mid+1,cmp_y);sort(c+mid+1,c+r+1,cmp_y);
	int i = mid+1,j = l;
	while(i <= r){
		while(j <= mid && c[i].y >= c[j].y){
			Add(c[j].z,c[j].size);
			j++;
		}
		c[i].ans += get_sum(c[i].z);
		i++;
	}
	for(int h = l; h < j; h++){
		Add(c[h].z,-c[h].size);
	}
}
int main(){
//	freopen("in.txt","r",stdin);
//	freopen("out.txt","w",stdout);
	cin>>n>>k;
	for(int i=1; i<=n; i++){
		cin>>a[i].x>>a[i].y>>a[i].z;
	}
	sort(a+1,a+n+1,cmp_x);
	c[++cnt] = a[1];
	c[cnt].size = 1;
	for(int i=2; i<=n; i++){
		if(a[i].x != a[i-1].x || a[i].y != a[i-1].y || a[i].z != a[i-1].z){
			c[++cnt] = a[i];
			c[cnt].size = 1;
		}
		else{
			c[cnt].size++;
		}
	}
	cdq(1,cnt);
	for(int i=1; i<=cnt; i++){
		ans[c[i].ans + c[i].size - 1]+=c[i].size;
	}
	for(int i=0; i<n; i++){
		printf("%d\n",ans[i]);
	}
	return 0;
}