【学习笔记】莫队
本篇主要是我学习了莫队算法之后的一些感受，仅包含普通莫队与普通带修改莫队相关知识，望各位大佬指点一二
首先就是非常经典的莫队适用的题型：
（1）区间询问问题，且区间信息不可高效合并，即传统数据结构难以维护
（2）必须可以离线
（3）不带修改（或带简单修改）
（4）（这一条可以自动忽略）若已知区间 \([L_1,R_1]\) 的答案，我们可以花费 \(O(|L_1 - L_2|)\) 的时间将左端点移到 \(L_2\)，花费 \(O(|R_1 - R_2|)\) 的时间将右端点移到 \(R_2\) 的位置，从而得到区间 \([L_2,R_2]\) 的答案，即我们区间左右端点移动 \(1\) 的复杂度是 \(O(1)\) 的
下面就来说一下莫队的基本思想：
在我们可以 \(O(1)\) 地移动区间左右端点地前提下，莫队就是将所有的询问区间按照一定顺序排好，然后从第一个区间开始进行区间的移动，每次移动完一个区间就进行答案的统计，每一个区间的答案从上一个移动好的区间移动过去，而非从头开始重新移动，我们一开始认为已知 \([0,0]\) 的答案
对于莫队分块的大小：
普通莫队：\(\sqrt n\)
带修莫队：\(n^{\frac{2}{3}}\)
四指针莫队：\(n^{\frac{3}{4}}\)
普通莫队
看思想肯定是啥都不会的，下面就通过一道题具体来看一下什么是莫队（相信我莫队真的不难）
题目描述：
基本思路：
我们在本题中维护数组 \(tmp[i]\) 表示数 \(i\) 出现的次数，在移动区间的过程中对这个数组进行操作，若 \(tmp[i]\) 在加入了一次 \(i\) 之后为 \(1\) 则为出现了一个新数，同理若 \(tmp[i]\) 在删去了一个 \(i\) 之后为 \(0\) 则为消失了一个数，然后按照莫队的基本写法写就好了
代码实现：
文本版：
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 5e4+5;
const int MAXM = 2e5+5;
const int MAX_VAL = 1e6+5;
struct node{
int l,r,pos,id;
}q[MAXM];
int a[MAXN],ans[MAXM],tmp[MAX_VAL],n,S,m,res;
int bl(int x){
return (x - 1) / S + 1;
}
bool cmp(node l,node r){
if(bl(l.l) != bl(r.l))
return bl(l.l) < bl(r.l);
return l.r < r.r;
}
void Dele(int val){
if((--tmp[val]) == 0)
res--;
}
void Add(int val){
if((++tmp[val]) == 1)
res++;
}
int main(){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
cin>>n;
S = sqrt(n);
for(int i=1; i<=n; i++){
cin>>a[i];
}
cin>>m;
for(int i=1; i<=m; i++){
cin>>q[i].l>>q[i].r;
q[i].pos = i;
}
sort(q+1,q+m+1,cmp); //按照第一关键字块内顺序，第二关键字大小顺序排序
int now_l = 0,now_r = 0;
for(int i=1; i<=m; i++){
while(now_l > q[i].l) Add(a[--now_l]); //因为这个数我们加过了，所以加减过后的
while(now_r < q[i].r) Add(a[++now_r]);
while(now_l < q[i].l) Dele(a[now_l++]); //因为这个数我们也要删除，所以先删再加
while(now_r > q[i].r) Dele(a[now_r--]);
ans[q[i].pos] = res;
}
for(int i=1; i<=m; i++){
cout<<ans[i]<<endl;
}
return 0;
}
代码部分说明：
\(bl(i)\) 返回的是分块之后 \(i\) 所在块的编号
这也就是普通莫队的写法，对于不同的题目唯一需要修改的也就是 \(Add\) 函数和 \(Dele\) 函数而已。
需要注意的一点（也是我之前不知道的一点）：在莫队的扩展区间要先进行 \(l--\),\(r++\) 然后再进行 \(l++\),\(r--\)，为了避免出现比如 \([5,3]\) 这种的恶心情况
带修改莫队
带修改莫队与普通莫队基本是一致的，推荐理解了普通莫队之后再进行观看。
带修莫队会比普通莫队多维护一个值：时间戳，说白了就是这个询问在第几次修改后，那么在我们进行区间移动的时候，只需要在移动完区间之后，再移动一下时间戳，使得时间戳也符合当前询问的条件就好了。
下面依旧是通过一道题来具体的看看带修莫队：
题目描述：
基本思路：
使用带修莫队，与普通莫队一样维护一个 \(tmp\) 数组， \(tmp[i]\) 表示数 \(i\) 出现的次数，然后按上一道题的写法写就好了，就是移动区间的时候需要移动时间戳
代码实现：
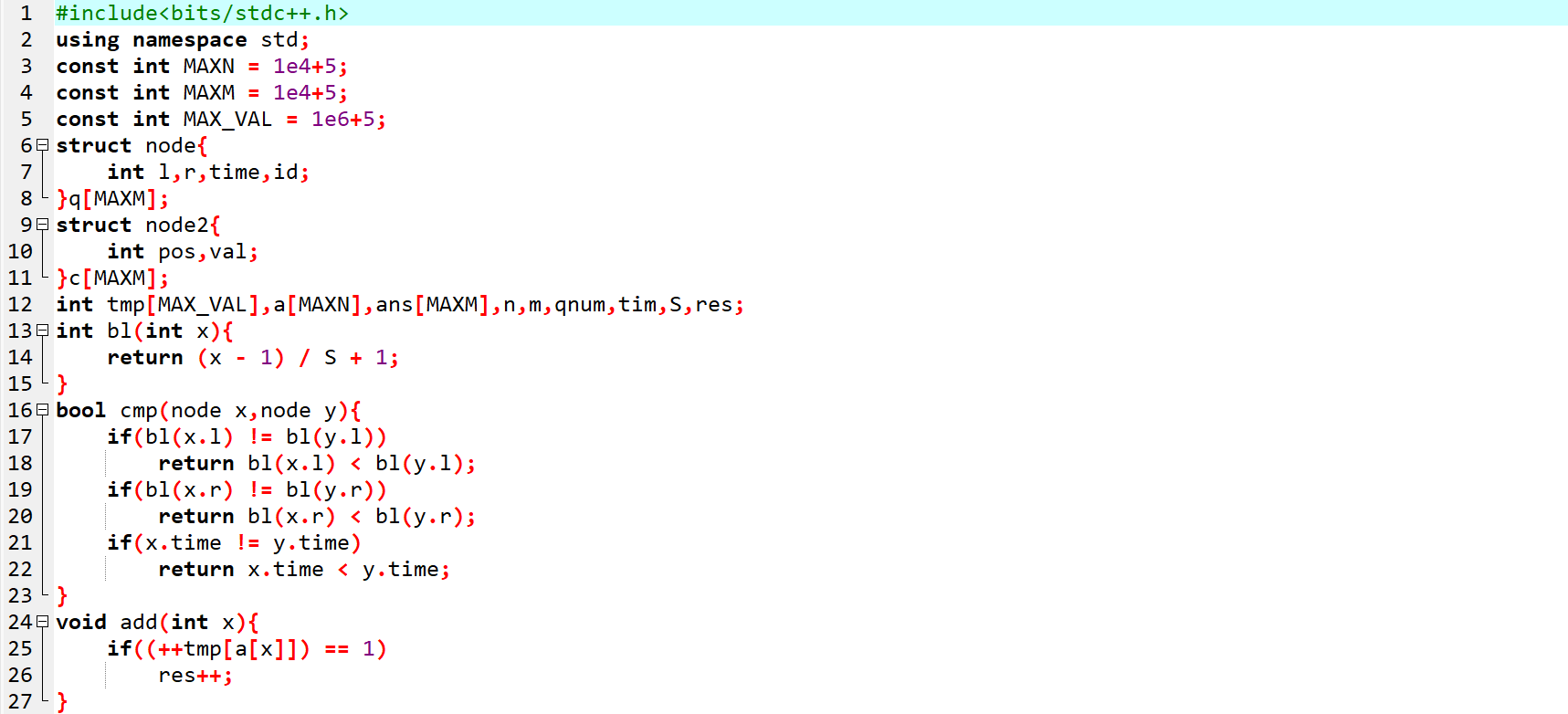
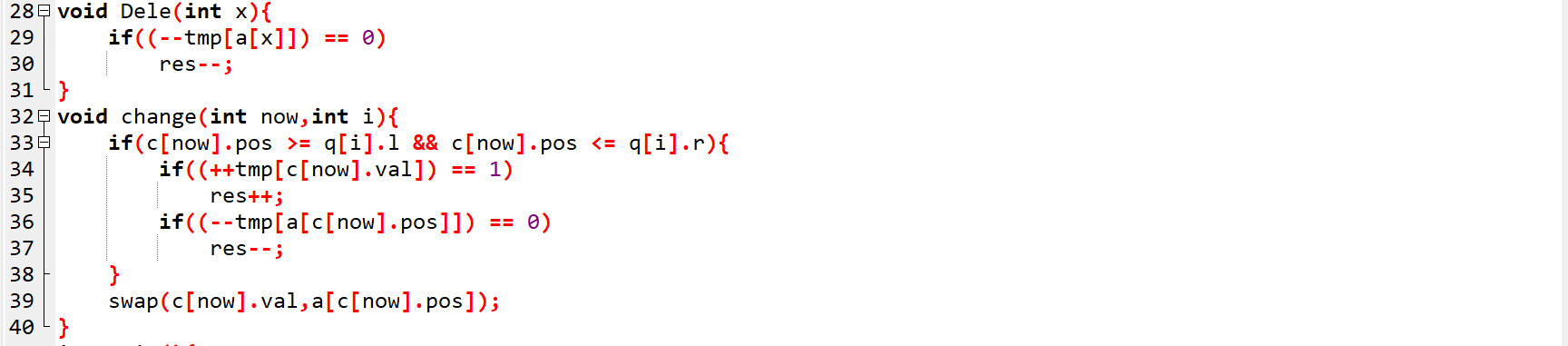
文本版：
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e4+5;
const int MAXM = 1e4+5;
const int MAX_VAL = 1e6+5;
struct node{
int l,r,time,id;
}q[MAXM];
struct node2{
int pos,val;
}c[MAXM];
int tmp[MAX_VAL],a[MAXN],ans[MAXM],n,m,qnum,tim,S,res;
int bl(int x){
return (x - 1) / S + 1;
}
bool cmp(node x,node y){
if(bl(x.l) != bl(y.l))
return bl(x.l) < bl(y.l);
if(bl(x.r) != bl(y.r))
return bl(x.r) < bl(y.r);
if(x.time != y.time)
return x.time < y.time;
}
void add(int x){
if((++tmp[a[x]]) == 1)
res++;
}
void Dele(int x){
if((--tmp[a[x]]) == 0)
res--;
}
void change(int now,int i){
if(c[now].pos >= q[i].l && c[now].pos <= q[i].r){
if((++tmp[c[now].val]) == 1)
res++;
if((--tmp[a[c[now].pos]]) == 0)
res--;
}
swap(c[now].val,a[c[now].pos]);
}
int main(){
// freopen("in.txt","r",stdin);
// freopen("out.txt","w",stdout);
cin>>n>>m;
S = int(pow(n,0.66));
for(int i=1; i<=n; i++){
cin>>a[i];
}
for(int i=1; i<=m; i++){
char opt;
int x,y;
cin>>opt>>x>>y;
if(opt == 'Q'){
q[++qnum].l = x;
q[qnum].r = y;
q[qnum].time = tim;
q[qnum].id = qnum;
}
else if(opt == 'R'){
c[++tim].pos = x;
c[tim].val = y;
}
}
sort(q+1,q+qnum+1,cmp);
int now = 0,now_l = 0,now_r = 0;
for(int i=1; i<=qnum; i++){
while(q[i].l < now_l) add(--now_l);
while(q[i].r > now_r) add(++now_r);
while(q[i].l > now_l) Dele(now_l++);
while(q[i].r < now_r) Dele(now_r--);
while(q[i].time < now) change(now--,i); //非常好的一句话：改多了，改回去，所以 now 点也要改回去
while(q[i].time > now) change(++now,i); //改少了，改过来，now 点已经改过了，所以不用了
ans[q[i].id] = res;
}
for(int i=1; i<=qnum; i++){
cout<<ans[i]<<endl;
}
return 0;
}
代码部分说明：
其他的我就不多说了，我们仔细读读代码就明白了，关于 \(change\) 函数最后的 \(swap\) 操作的说明，我们在移动时间戳的时候第一次处理这个修改即会将 \(a\) 中对应的值改为 \(c\) 中对应的值，而当我们第二次要处理这个修改就是相当于我们搞回去了，也就是这个修改不要了，所以对于第二次就是将 \(a\) 中对应的值改回去，也就是改成交换后 \(c\) 里的值，交换之后再次修改就可以实现这个功能
