【学习笔记】分块
蒟蒻最近几天搞了一下分块算法，有一些感受，就在这里一起说了。
首先就是十分经典的分块与传统数据结构的对比：
（1）传统数据结构的复杂度：\(O(log_{2}n)\) 而分块复杂度：\(O(\sqrt n)\)
（2）传统数据结构维护的区间要求维护的信息可以高效合并，分块可以维护不可以高效合并的信息
分块因为不像数据结构可以非常模板化的一个东西，虽然也比较模板，但是格式上也比较随意，下面也就来稍微说说分块的思想
分块就是按照一定的大小（一般是 \(\sqrt n\)），将原序列分成一个个块，然后以块为单位处理与我们维护的信息有关的部分信息，然后对于查询操作就是将这个区间里整块的信息，也就是我们之前处理过的东西直接拿来用，然后没有处理过的，也就是这个区间的边角部分暴力进行求解。
考虑复杂度的证明：因为我们最多有 \(\sqrt n\) 个块，对于每一个我们询问的区间，其边角的部分，也就是不属于整块的部分最多 \(2 \times \sqrt n\) 个，所以我们询问一次的复杂度最多也就是 \(3 \times \sqrt n\) (当然不可能是这个数，肯定会小)，我们的复杂度也是 \(O(\sqrt n)\) 级
相信大家肯定看的不是很明白，不大会实现，其实分块就跟暴力是差不多的，那么下面就通过一道例题来具体看看分块的写法
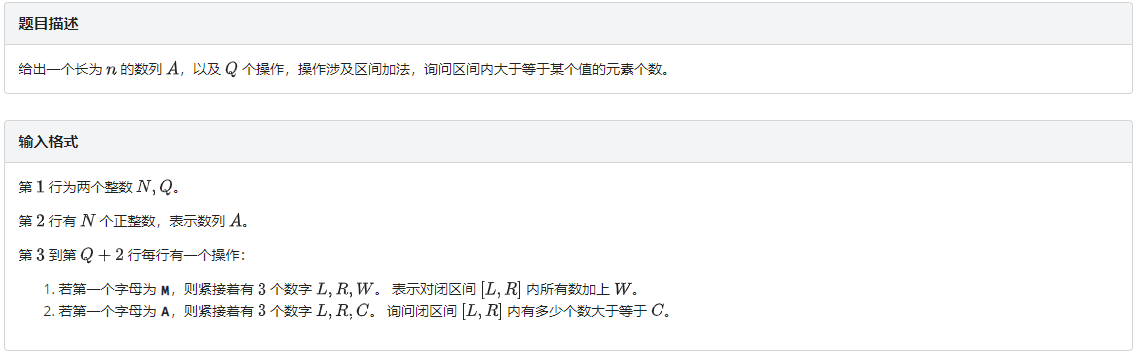
基本思路：
对于查询操作：每一个块都维护另一个数组，这个数组是一个排好序的数组，就是这个块内元素按顺序排列，对于整块直接二分查找有多少数大于等于 \(C\)，这样我们最多 \(\sqrt n\) 个块，每个块二分的复杂度为 \(\log_{2}n\) ，剩下的不属于整块的部分暴力找就好，所以单次查询的复杂度为 \(O(\sqrt n · \log_{2}n)\)
对于修改操作：每个整块我们都采取打标记的方式，表示这一个整块被加了多少，然后对于边角的部分我们就暴力加，注意暴力加完了之后还需要维护好我们的排序后的数组，这样单次修改的复杂度就是 \(O(\sqrt n)\)
所以整体 \(q\) 次查询的复杂度就是：\(O(q·\sqrt n·\log_{2}n)\)
看思路肯定是打不出代码的，下面来放一下代码：
方便直接复制下面放文本版：
#include<bits/stdc++.h>
using namespace std;
const int MAXN = 1e6+5;
int n,q,S,tot,bl[MAXN],br[MAXN],sa[MAXN],a[MAXN],tag[MAXN];
void sort_block(int x){
for(int i=bl[x]; i<=br[x]; i++)
sa[i] = a[i];
sort(sa+bl[x],sa+br[x]+1);
}
void prework(){
for(int i=1; i<=n; i++){
if(i % S == 1){
br[tot] = i-1;
bl[++tot] = i;
}
}
br[tot] = n;
br[tot+1] = bl[tot+1] = n+1;
for(int i=1; i<=tot; i++)
sort_block(i);
}
void add_val(int l,int r,int val){
int L = (l-1) / S + 1,R = (r-1) / S + 1;
if(r - l + 1 <= 2 * S){
for(int i=l; i<=r; i++){
a[i]+=val;
}
for(int i=L; i<=R; i++)
sort_block(i);
}
else{
bool tagl = true,tagr = true;
if(l == bl[L]){
tagl = false;
L--;
}
if(r == br[R]){
tagr = false;
R++;
}
for(int i = L+1; i<=R-1; i++){
tag[i]+=val;
}
for(int i=l; i<=br[L]; i++){
a[i]+=val;
}
if(tagl) sort_block(L);
for(int i=bl[R]; i<=R; i++){
a[i]+=val;
}
if(tagr) sort_block(R);
}
}
int find(int x,int val){
int l = bl[x],r = br[x],ans = br[x] + 1,mid = (l+r)>>1;
while(l <= r){
mid = (l+r)>>1;
if(sa[mid] >= val){
ans = mid;
r = mid-1;
}
else{
l = mid+1;
}
}
return br[x] - ans + 1;
}
int query(int l,int r,int val){
int L = (l - 1) / S + 1,R = (r - 1) / S + 1,ans = 0;
if(r - l + 1 <= 2 * S){
for(int i=l; i<=r; i++){
if(a[i] + tag[(i-1) / S + 1] >= val)
ans++;
}
return ans;
}
else{
if(l == bl[L]) L--;
if(r == br[R]) R++;
for(int i=L+1; i<=R-1; i++){
ans += find(i,val - tag[i]);
}
for(int i=l; i<=br[L]; i++){
if(a[i] + tag[L] >= val)
ans++;
}
for(int i = bl[R]; i<=r; i++){
if(a[i] + tag[R] >= val){
ans++;
}
}
return ans;
}
}
int main(){
cin>>n>>q;
for(int i=1; i<=n; i++){
cin>>a[i];
}
S = sqrt(n);
prework();
while(q--){
char opt;
int l,r,x;
cin>>opt>>l>>r>>x;
if(opt == 'M'){
add_val(l,r,x);
}
else if(opt == 'A'){
printf("%d\n",query(l,r,x));
}
}
return 0;
}
其实分块的代码也不用我多说，咱们仔细地看一看也就能看懂了，因为分块的思路就相当于暴力
