【题解】金牌导航 启发式合并-连通性询问

题面：

---

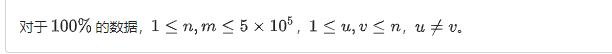
注意本题强制在线

做法详解：

---

一看到每一次加一条边，询问某两个点的联通的就自然而然地能想到使用并查集。
我们考虑最暴力的做法：
每一次从第一条边开始依次加边，直到某次加边之后 \(u,v\) 联通
显然这样做是不可以的，很明显我们不可能每一次都从头加一遍边，所以就考虑这样直接来一条边加一条然后维护一个其他的信息。
我们考虑并查集使用按秩合并，对于一个合并 \(y\) 合并到 \(x\) 里，我们考虑维护一个数组 val[y] 代表直接合并 \(y\) 地这一个合并是第几次合并，也就是第几条加入的边，因为我们的每一个点会且仅会被当作子树直接合并一次，所以这个数组的值也是确定的。这样就考虑对于每一组询问该如何去回答.
我们能发现一个很奇妙的性质，对于使 \(u,v\) 联通有贡献的边,一定在且仅在并查集中它们之间的唯一路径上，就是只有这些边对他们的联通有帮助，其他的边无论存在与否都是无用的(仔细思考一下,最重要的一点)，那么答案也就是这些对它们的联通有帮助的这些边的编号的最大值，因为只有这些边都被选择 \(u,v\) 才联通，所以答案也就是这些边中最后一个被加入的边
现在的问题就是如何去找它们在并查集上的唯一路径，这个时候其实我们的按秩合并的作用就体现出来了,我们能发现按秩合并的并查集，任何一条从根出发的链的长度都不会超过 \(log_{2}n\) ，所以我们可以直接从这两个点暴力向上跳，然后将经过的边取最大值就好了，暴力向上跳还是有一些细节的,具体见代码.
时间复杂度: \(O(mlog_{2}n)\)

AC代码:（是不是看着舒服多了）

---