14 深度学习-卷积

1.简述人工智能、机器学习和深度学习三者的联系与区别。

	人工智能	机器学习	深度学习
联系	人工智能是最早出现的，也是最大、最外侧的同心圆；其次是机器学习，稍晚一点；最内侧，是深度学习，也是当今人工智能大爆炸的核心驱动。 人工智能>机器学习>深度学习
区别	为机器赋予人的智能，是目的，是结果，适用图像分类、人脸识别	一种实现人工智能的方法，应用领域是计算机视觉	一种实现机器学习的技术，适合处理大数据

 

2. 全连接神经网络与卷积神经网络的联系与区别。

	全连接神经网络	卷积神经网络
含义	全连接神经网络(DNN)是最朴素的神经网络，它的网络参数最多，计算量最大。	卷积神经网络是一种深度前馈人工神经网络，已成功地应用于图像识别。
联系	结构相似，输入输出以及训练的流程也基本一致。
区别	每层隐藏层的每个神经元都和相邻隐藏层的所有神经元相连接。	不是全连接的，隐藏层的每个神经元只是和上一个隐藏层某一小片相连。 卷积神经网络可以更好的处理图像数据。

 

 3.理解卷积计算。

以digit0为例，进行手工演算。

from sklearn.datasets import load_digits #小数据集8*8

digits = load_digits()

0	0	5	13	9	1	0	0
0	0	13	15	10	15	5	0
0	3	15	2	0	11	8	0
0	4	12	0	0	8	8	0
0	5	8	0	0	9	8	0
0	4	11	0	1	12	7	0
0	2	14	5	10	12	0	0
0	0	6	13	10	0	0	0

（参考：https://blog.csdn.net/leviopku/article/details/80327478）

通常用外部api进行卷积的时候，会面临mode选择，full、same、valid，这三种不同模式是对卷积核移动范围的不同限制。

扫描图片时划过像素的个数影响卷积后长度，默认1个像素。

公式：新图片尺寸=[(原图片尺寸-卷积核尺寸+2*像素数)/步长]+1（先取整数再+1）

可以指定步长（精细度） 

已知原图片尺寸为8*8，设卷积核尺寸是3x3，步长是1。

卷积核为：

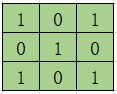
（1）Full

 

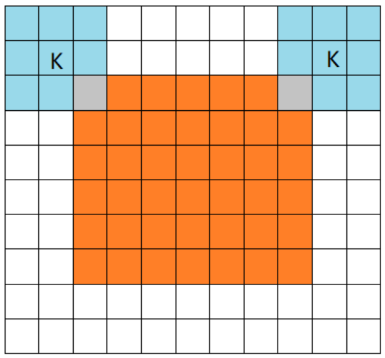
橙色部分为image， 蓝色部分为filter。full模式的意思是，从filter和image刚相交开始做卷积，白色部分为填0。

结果：8*8->10*10 变大

（2）Same：保留边界处的卷积结果

 

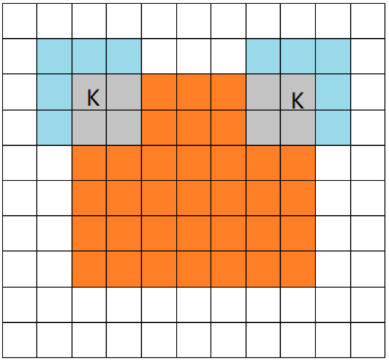
当filter的中心(K)与image的边角重合时，开始做卷积运算，可见filter的运动范围比full模式小了一圈。

注意：这里的same还有一个意思，卷积之后输出的feature map尺寸保持不变(相对于输入图片)。当然，same模式不代表完全输入输出尺寸一样，也跟卷积核的步长有关系。

same模式也是最常见的模式，因为这种模式可以在前向传播的过程中让特征图的大小保持不变，调参师不需要精准计算其尺寸变化(因为尺寸根本就没变化)。
结果：8*8->8*8 不变

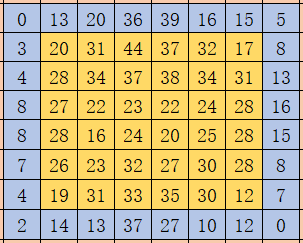
（3）Valid：只进行有效的卷积，对边界数据不处理

 

 当filter全部在image里面的时候，进行卷积运算，可见filter的移动范围较same更小了。

结果：8*8->6*6 变小

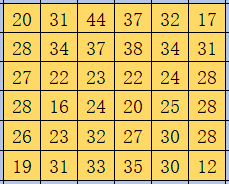
4.理解卷积如何提取图像特征。

读取一个图像；

以下矩阵为卷积核进行卷积操作；

显示卷积之后的图像，观察提取到什么特征。

卷积API

scipy.signal.convolve2d

tf.keras.layers.Conv2D

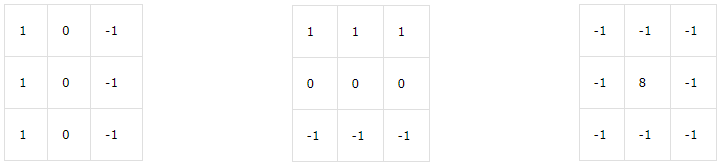
from PIL import Image
import numpy as np
from scipy.signal import convolve2d
import matplotlib.pyplot as plt

# 读取一个图像
I = Image.open(r'C:\Users\lenovo\Pictures\Saved Pictures\3.jpg')
L = I.convert('L')

img=np.array(I)  # img原图 
imgg=np.array(L) # imgg灰度图

# 以下矩阵为卷积核进行卷积操作
k1=np.array([[1,0,-1],[1,0,-1],[1,0,-1]])       # 垂直边缘检测
k2=np.array([[1,1,1],[0,0,0],[-1,-1,-1]])       # 水平边缘检测
k3=np.array([[-1,-1,-1],[-1,8,-1],[-1,-1,-1]])  # 检测中间

# imgg：二维数组，k1：卷积核，boundary：边界填充方式，mode卷积类型
img1 = convolve2d(imgg,k1,boundary='symm',mode='same')
img2 = convolve2d(imgg,k2,boundary='symm',mode='same')
img3 = convolve2d(imgg,k3,boundary='symm',mode='same')

# 显示卷积之后的图像
plt.matshow(img)   
plt.matshow(imgg)  
plt.matshow(img1)  
plt.matshow(img2)  
plt.matshow(img3)  

原图

灰度图

垂直边缘检测                                       水平边缘检测                                        中心边缘检测

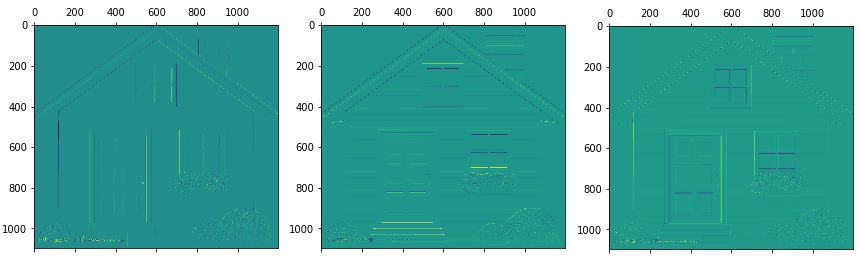
垂直边缘检测：可以看出图片中物体的垂直方向边界特征被提取出来，而其他的特征被弱化了。

水平边缘检测：可以看出图片中物体的水平方向边界特征被提取出来，而其他的特征被弱化了。

中心边缘检测：可以看出图片中物体的中心边界特征被提取出来，而四周边界的特征被弱化了。

 

5. 安装Tensorflow,keras

参考：https://blog.csdn.net/u011119817/article/details/88309256

用conda安装可以判断所有安装包的版本间的兼容性。

 

6. 设计手写数字识别模型结构，注意数据维度的变化。

from tensorflow.keras.models import Sequential

from tensorflow.keras.layers import Dense， Flatten, Conv2D, MaxPool2D

model = tf.keras.Sequential()

model.add(Conv2D(…))

model.add(MaxPool2D(…))

...

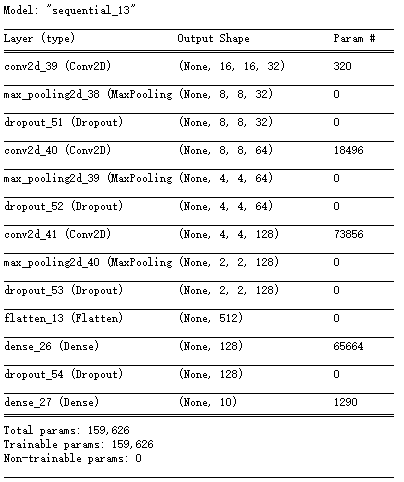
#可以上传手动演算的每层数据结构的变化过程。model.summary() 

 

# 导入相关包
# sequential设计层数
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense,Dropout,Flatten,Conv2D,MaxPool2D

#建立模型
model=Sequential()

ks=(3,3)   # 卷积核大小
ips=(16,16,1)

#一层卷积
model.add(
    Conv2D(filters=32,          # 卷积核的个数
           kernel_size=ks,     # 卷积核大小
           padding='same',     # 保证卷积核大小，不够不算
           input_shape=ips,    
           activation='relu')) # activation: 激活函数，'relu','sigmoid'等

#池化层1
model.add(MaxPool2D(pool_size=(2,2)))
model.add(Dropout(0.25))

#二层卷积
model.add(
    Conv2D(filters=64,kernel_size=ks,padding='same',activation='relu'))
#池化层2
model.add(MaxPool2D(pool_size=(2,2)))
model.add(Dropout(0.25))

#三层卷积
model.add(
    Conv2D(filters=128,kernel_size=ks,padding='same',activation='relu'))
#池化层3
model.add(MaxPool2D(pool_size=(2,2)))
model.add(Dropout(0.25))


model.add(Flatten()) #平坦层
model.add(Dense(128,activation='relu')) #dense全连接层
model.add(Dropout(0.25))
model.add(Dense(10,activation='softmax')) #激活函数  softmax分类

model.summary()

 

参考：

https://www.jianshu.com/p/afe485aa08ce

https://blog.csdn.net/junjun150013652/article/details/82217571