5 线性回归算法
1.本节重点知识点用自己的话总结出来,可以配上图片,以及说明该知识点的重要性
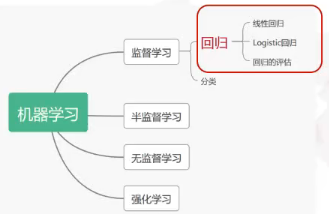
回归问题的判定:

回归和分类的区别:

应用:房价预测、销售额预测、贷款额度的预测等。
单因素影响的一元线性模型例子:房价预测。
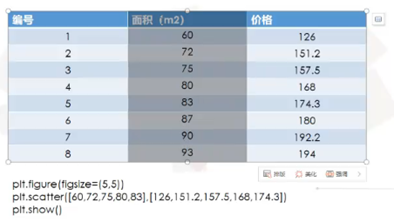
横坐标为房子面积,纵坐标为价格。

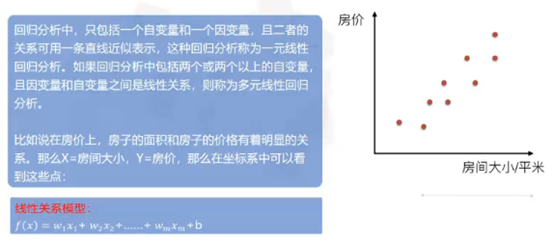
线性回归的定义:通过一个或多个自变量与因变量之间进行建模的回归方法,其中一个可以为一个或者多个自变量之间的线性组合。


数组(numpy:ndarray)分为:加汰,乘汰。
0维 1, 2, 3
1维 [ 1, 2, 3 ]
2维 [ [ 1, 2, 3 ], [1 ,2 ,3 ] ]
3维 [ [ [ 1, 2, 3 ], [1, 2, 3 ] ],
[ [ 1, 2, 3 ], [1, 2, 3 ] ] ]
矩阵
(1)矩阵必须是2维的。
(2)矩阵满足了特殊的运算要求:
矩阵的乘法:(m行,h列)*(h行,n列)=(m,n)
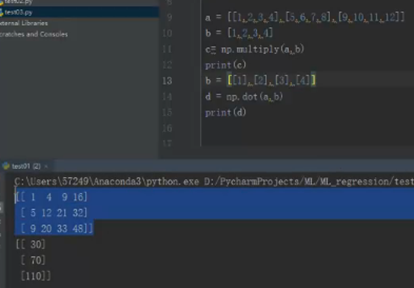
c是a和b的数组乘积,结果是3行4列
d是a和b的矩阵乘积,结果是3行1列
30 = 1*1+2*2+3*3+4*4
= 1+4+9+16
70 = 1*5+2*6+3*7+4*8
= 5+12+21+32
110 = 1*9+2*10+3*11+4*12
=9+20+33+48
满足线性回归的要求。
y =w*x+b(w权重,x为特征--房子面积)
机器预测值和真实值也是存在一定误差的。
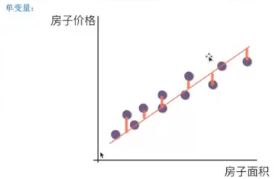
有误差需要迭代算法减小误差。





代码实现梯度下降例子:
1 import matplotlib.pyplot as plt
2 import random
3
4 _xs = [0.1*x for x in range(0, 10)]
5 _ys = [12*i+4 for i in _xs]
6 print(_xs)
7 print(_ys)
8
9 w = random.random() # 权重
10 b = random.random() # 间距
11 a1 = []
12 b1 = []
13 for i in range(100): # 训练次数
14 for x, y in zip(_xs, _ys): # 让分别遍历上面的数据
15 o = w*x+b # o代表预测值
16 e = (o-y) # 误差 预测值减去标签 有+-
17 loss = e**2 # 误差平方等于损失
18 dw = 2*e*x # 对w求导
19 db = 2*e*1 # 对b求导
20 w = w - 0.1*dw # 梯度下降
21 b = b - 0.1*db # 学习率为0.1
22 print('loss={0},w={1},b={2}'.format(loss, w, b))
23 a1.append(i)
24 b1.append(loss)
25 plt.plot(a1, b1)
26 plt.pause(0.1)
27 plt.show()
数据:
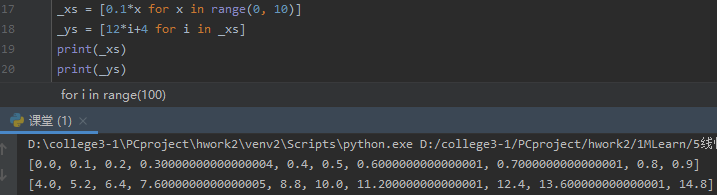
10次

50次

100次

10次 50次
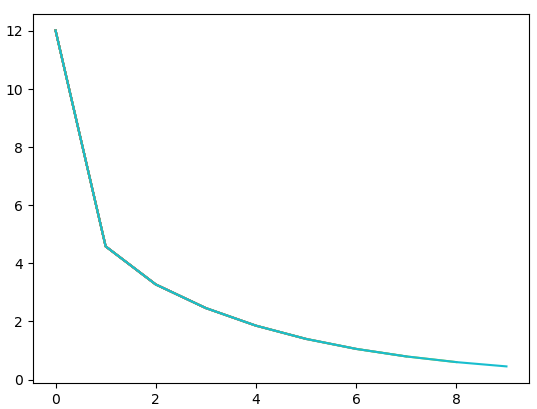
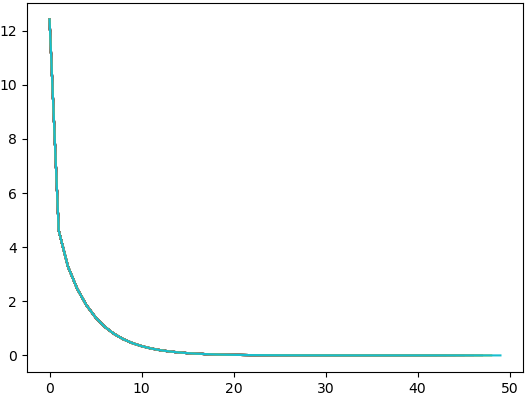
100次
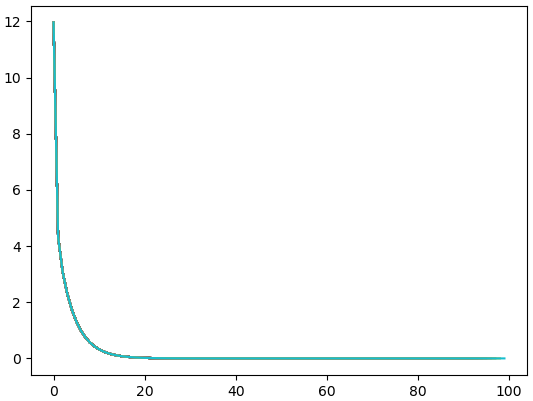
迭代算法减少损失,减小误差。
线性回归可以找到规律,预测趋势,或者说是对数据找一个合适的表达式来表达某一个趋势。对于我们的生活,在预测房价,预测投资风险,预测空气质量等多领域有重要的意义。
2.思考线性回归算法可以用来做什么?(大家尽量不要写重复)
预测身高体重,预测空气质量,预测投资风险,预测票房,预测产品销售量等。
3.自主编写线性回归算法 ,数据可以自己造,或者从网上获取。(加分题)
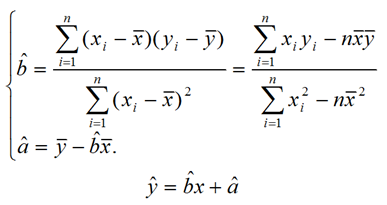

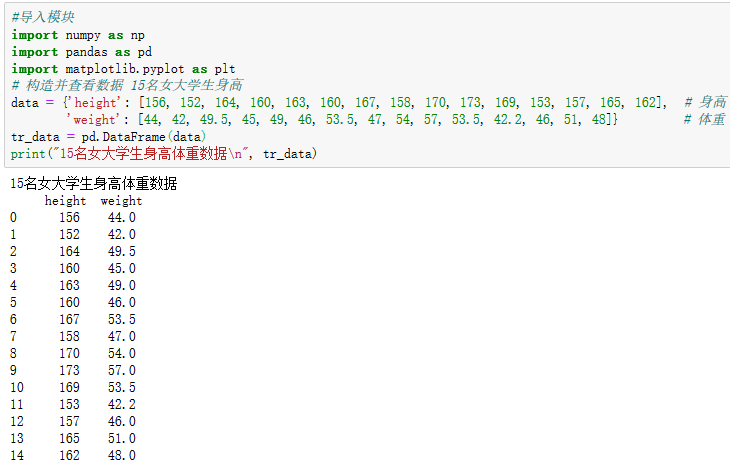
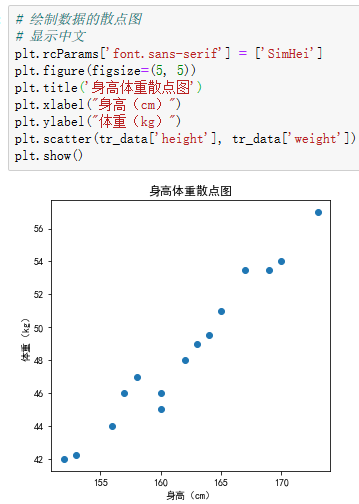

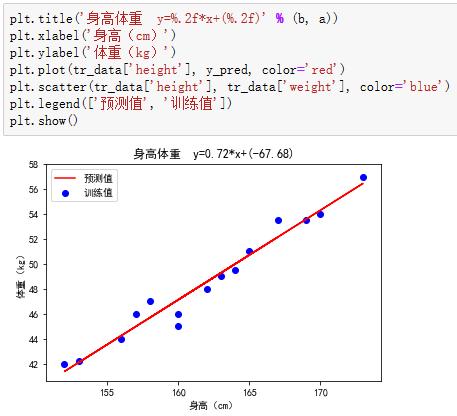
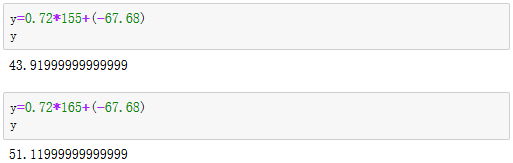
算出女大学生根据身高猜测体重的函数y=0.72*x+(-67.68)。
若以此为标准,猜测身高为155或165女大学生的体重为: