Python数据结构——二叉树的实现

1. 二叉树

二叉树(binary tree)中的每个节点都不能有多于两个的儿子。

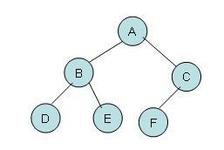
1.1 二叉树列表实现

如上图的二叉树可用列表表示：

tree=['A',  #root
      ['B',    #左子树
       ['D',[],[]],
       ['E',[],[]]],
      ['C',     #右子树
       ['F',[],[]],
       []]
      ]

实现：

def BinaryTree(item):
    return [item,[],[]]
def insertLeft(tree,item):
    leftSubtree=tree.pop(1)
    if leftSubtree:
        tree.insert(1,[item,leftSubtree,[]])
    else:
        tree.insert(1,[item,[],[]])
    return tree
def insertRight(tree,item):
    rightSubtree=tree.pop(2)
    if rightSubtree:
        tree.insert(2,[item,[],rightSubtree])
    else:
        tree.insert(2,[item,[],[]])
    return tree
def getLeftChild(tree):
    return tree[1]
def getRightChild(tree):
    return tree[2]

要实现下图的树：

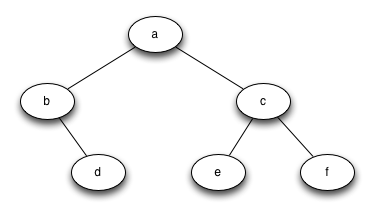
tree=BinaryTree('a')
insertLeft(tree,'b')
insertRight(tree,'c')
insertRight((getLeftChild(tree)),'d')
insertLeft((getRightChild(tree)),'e')
insertRight((getRightChild(tree)),'f')

1.2 二叉树的类实现

class BinaryTree(object):
    def __init__(self,item):
        self.key=item
        self.leftChild=None
        self.rightChild=None
    def insertLeft(self,item):
        if self.leftChild==None:
            self.leftChild=BinaryTree(item)
        else:
            t=BinaryTree(item)
            t.leftChild=self.leftChild
            self.leftChild=t
    def insertRight(self,item):
        if self.rightChild==None:
            self.rightChild=BinaryTree(item)
        else:
            t=BinaryTree(item)
            t.rightChild=self.rightChild
            self.rightChild=t

2. 表达式树

表达式树(expression tree)的树叶是操作数，其他节点为操作符。

图 ((7+3)*(5-2))的表达式树表示

2.1 根据中缀表达式构造表达式树：

遍历表达式：

1.建立一个空树

2.遇到'('，为当前的Node添加一个left child，并将left child当做当前Node。

3.遇到数字，赋值给当前的Node，并返回parent作为当前Node。

4.遇到('+-*/')，赋值给当前Node，并添加一个Node作为right child，将right child当做当前的Node。

5.遇到')',返回当前Node的parent。

def buildexpressionTree(exp):
    tree=BinaryTree('')
    stack=[]
    stack.append(tree)
    currentTree=tree
    for i in exp:
        if i=='(':
            currentTree.insertLeft('')
            stack.append(currentTree)
            currentTree=currentTree.leftChild
        elif i not in '+-*/()':
            currentTree.key=int(i)
            parent=stack.pop()
            currentTree=parent
        elif i in '+-*/':
            currentTree.key=i
            currentTree.insertRight('')
            stack.append(currentTree)
            currentTree=currentTree.rightChild
        elif i==')':
            currentTree=stack.pop()
        else:
            raise ValueError
    return tree

上述算法对中缀表达式的写法要求比较繁琐，小括号应用太多，例如要写成(a+(b*c))的形式。

用后缀表达式构建表达式树会方便一点:如果符号是操作数，建立一个单节点并将一个指向它的指针推入栈中。如果符号是一个操作符，从栈中弹出指向两棵树T1和T2的指针并形成一棵新的树，树的根为此操作符，左右儿子分别指向T2和T1.

def build_tree_with_post(exp):
    stack=[]
    oper='+-*/'
    for i in exp:
        if i not in oper:
            tree=BinaryTree(int(i))
            stack.append(tree)
        else:
            righttree=stack.pop()
            lefttree=stack.pop()
            tree=BinaryTree(i)
            tree.leftChild=lefttree
            tree.rightChild=righttree
            stack.append(tree)
    return stack.pop()

3.树的遍历

3.1 先序遍历(preorder travelsal)

先打印出根，然后递归的打印出左子树、右子树，对应先缀表达式

def preorder(tree,nodelist=None):
    if nodelist is None:
        nodelist=[]
    if tree:
        nodelist.append(tree.key)
        preorder(tree.leftChild,nodelist)
        preorder(tree.rightChild,nodelist)
    return nodelist

3.2 中序遍历(inorder travelsal)

先递归的打印左子树，然后打印根，最后递归的打印右子树，对应中缀表达式

def inorder(tree):
    if tree:
        inorder(tree.leftChild)
        print tree.key
        inorder(tree.rightChild)

3.3 后序遍历(postorder travelsal)

递归的打印出左子树、右子树，然后打印根，对应后缀表达式

def postorder(tree):
    if tree:
        for key in postorder(tree.leftChild):
            yield key
        for key in postorder(tree.rightChild):
            yield key
        yield tree.key

3.4 表达式树的求值

def postordereval(tree):
    operators={'+':operator.add,'-':operator.sub,'*':operator.mul,'/':operator.truediv}
    leftvalue=None
    rightvalue=None
    if tree:
        leftvalue=postordereval(tree.leftChild)
        rightvalue=postordereval(tree.rightChild)
        if leftvalue and rightvalue:
            return operators[tree.key](leftvalue,rightvalue)
        else:
            return tree.key