先序中序求解二叉树（使用二叉查找树原理）

　　　 二叉树的先序中序序列确定，二叉树也就确认了，但还原二叉树确实有点麻烦，要不断的遍历中序序列。后来学习了二叉查找树，发现了一个很巧的办法。

　　　 二叉查找树的特性是每个节点都有权值，其规律为左子节点小于父节点，右子节点大于父节点，其中序序列是有序的。如果我们把二叉树变成二叉查找树，就是要给每个子节点赋值，最简单的根据中序序列从0->赋值，现在我们来看看二叉查找树先序序列和二叉查找树的关系。以下树的中序序列为DBEGACF,附上权值为（D:0,B:1,E:2,G:3,A:4,C:5,F:6 ）

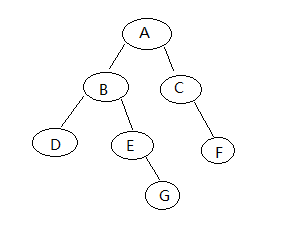
　　关于这个2插树先序为ABDEGCF,先序序列是先本身节点->左节点->有节点。细心发现二叉查找树的先序序列可以作为节点进入树的先后顺序（节点进入树的先后顺序可以有多个，不一定是先序序列），根据中序的赋值先序可以为4102356（与ABDEGCF相对应）也就是用这个序列来创建二叉查找树。接下来就不用我多说了。附上C#实现代码（PS:写算法不要用C#，坑）

namespace Test
{
    class Program
    {
        static void Main(string[] args)
        {
            string first = "ABDEGCF";           //先序
            string mid = "DBEGACF";             //中序
            DouBleTree doubletree = new DouBleTree(first,mid);
            Console.WriteLine(doubletree.FirstOrder());     //先序
            Console.WriteLine(doubletree.MidOrder());       //中序
            Console.WriteLine(doubletree.AfterOrder());     //后序
            Console.ReadLine();
        }
    }
    public class DouBleTree
    {
        /// <summary>
        /// 
        /// </summary>
        /// <param name="first">先序</param>
        /// <param name="mid">中序</param>
        public DouBleTree(string first, string mid)
        {
            tlist = new List<T>();
            for (int i = 0; i < mid.Length; i++)        //  附加权值
            {
                T t = new T
                {
                    data = mid[i],
                    WeigthValue = i,
                };
                tlist.Add(t);
            }
            doubleTreeRoot = new DoubleTreePoint        //创建根节点
            {
                data = first[0],
                WeightValue = tlist.FirstOrDefault(n => n.data == first[0]).WeigthValue,
            };
            for (int i = 1; i < first.Length; i++)      //创建二叉树
            {
                T t = tlist.FirstOrDefault(n => n.data == first[i]);
                doubleTreeRoot = InsertPoint(doubleTreeRoot, t);
            }
        }
        private DoubleTreePoint doubleTreeRoot;                                     //二叉树根节点
        private List<T> tlist;                                                      //给中序队列附权值
        private DoubleTreePoint InsertPoint(DoubleTreePoint point  ,T t)            //插入节点
        {
            if (point == null)
            {
                point = new DoubleTreePoint
                {
                    data = t.data,
                    WeightValue = t.WeigthValue,
                };
                return point;
            }
            if (point.WeightValue > t.WeigthValue)
            {
                 point.left = InsertPoint(point.left, t);
            }
            else
            {
                 point.right = InsertPoint(point.right, t);
            }
            return point;

        }
        public string FirstOrder()                      //返回先序队列
        {
            string str = "";
            First(doubleTreeRoot,ref str);
            return str;
        }
        private void First(DoubleTreePoint doubleTreePoint,ref string str)
        {
            if (doubleTreePoint == null) return;
            str += doubleTreePoint.data;
            First(doubleTreePoint.left,ref str);
            First(doubleTreePoint.right,ref str);
        }
        public string MidOrder()
        {
            string str = "";
            Mid(doubleTreeRoot, ref str);
            return str;
        }
        private void Mid(DoubleTreePoint doubleTreePoint,ref string str)
        {
            if (doubleTreePoint == null) return;
            Mid(doubleTreePoint.left,ref str);
            str += doubleTreePoint.data;
            Mid(doubleTreePoint.right,ref str);
        }
        public string AfterOrder()
        {
            string str = "";
            After(doubleTreeRoot,ref str);
            return str;
        }
        private void After(DoubleTreePoint doubleTreePoint,ref string str)
        {
            if (doubleTreePoint == null) return;
            After(doubleTreePoint.left,ref str);
            After(doubleTreePoint.right,ref str);
            str += doubleTreePoint.data;
        }
    }
    public class DoubleTreePoint
    {
        public char data { get; set; }          //数据
        public DoubleTreePoint left { get; set; }
        public DoubleTreePoint right { get; set; }
        public int WeightValue { get; set; }    //权值
    }
    public class T
    {
        public char data { get; set; }
        public int WeigthValue { get; set; } 
    }
}