C++ 算法竞赛、08 周赛篇 | AcWing 第94场周赛 ⭐

AcWing 第94场周赛

4870. 装物品 - AcWing题库

4870 装物品

4870. 装物品 - AcWing题库

巨简单题

#include <bits/stdc++.h>

using namespace std;

int main() {
    int n;
    cin >> n;
    if (n % 5 == 0)
        cout << (n / 5) << endl;
    else
        cout << (n / 5) + 1 << endl;

    return 0;
}

4871⭐⭐最早时刻

4871. 最早时刻 - AcWing题库

考查堆优化版迪杰斯特拉变形

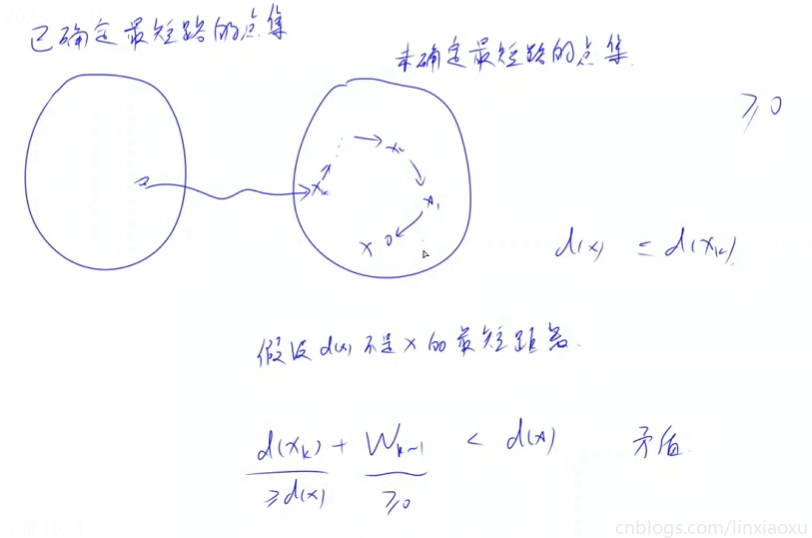
• 越早到达，越早离开 => 每个点维护一个最早到达时刻
• 如果 delay 小于 0，就不能用迪杰斯特拉算法

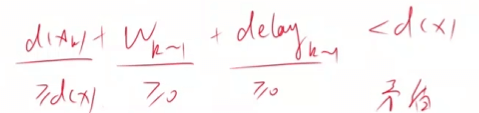
#include <bits/stdc++.h>
#define x first
#define y second

using namespace std;

int const N = 1e5 + 10, M = N << 1;
int const INF = 0x3f3f3f3f;
int h[N], e[M], ne[M], idx, w[M];
int dist[N];
bool st[N];
int n, m;
unordered_set<int> stop[N];
void add(int a, int b, int c) {
    e[idx] = b, ne[idx] = h[a], w[idx] = c, h[a] = idx++;
}

// 返回需要等待的时间
int next(int u, int t) {
    int cnt = 0;
    while (stop[u].count(t)) t++, cnt++;
    return cnt;
}

// 堆优化版迪杰斯特拉
typedef pair<int, int> PII;
int dijkstra() {
    priority_queue<PII, vector<PII>, greater<PII>> heap;
    memset(dist, 0x3f, sizeof dist);
    dist[1] = 0;
    heap.push({0, 1});
    while (heap.size()) {
        // 取最短路径
        auto t = heap.top();
        heap.pop();
        int u = t.y;
        // ^ 当前点是否已经走过
        if (st[u]) continue;
        // 记录当前点已经走过
        st[u] = true;
        // 更新其他路径
        int nw = next(u, dist[u]);
        for (int i = h[u]; ~i; i = ne[i]) {
            int j = e[i];
            if (dist[j] > dist[u] + w[i] + nw) {
                dist[j] = dist[u] + w[i] + nw;
                heap.push({dist[j], j});
            }
        }
    }
    if (dist[n] == INF)
        return INF;
    else
        return dist[n];
}

int main() {
    memset(h, -1, sizeof h);
    cin >> n >> m;
    for (int i = 0; i < m; i++) {
        int a, b, c;
        cin >> a >> b >> c;
        add(a, b, c);
        add(b, a, c);
    }
    for (int i = 1; i <= n; i++) {
        int k;
        cin >> k;
        while (k--) {
            int t;
            cin >> t;
            stop[i].insert(t);
        }
    }
    // 判断
    int ans = dijkstra();
    if (ans == INF) ans = -1;
    cout << ans << endl;

    return 0;
}

4872⭐⭐最短路之和

4872. 最短路之和 - AcWing题库

• 最终结果可能是 \(500^2 * 10^5\) 可能会爆int，需要用 long long 存
• 求任意 u，v 间的最短路径，需要用 Floyed 算法

• 每次删一个点，直到点删完
• 每次删一个点不太好做，可以倒过来，每次加一个点

弗洛伊德算法状态表示\(d(k,i,j\)) 是 所有从 i 出发，最终走到 j，且中间只经过节点编号不超过 k 的所有路径

外层循环按照加点的顺序循环，每次加点之后统计一下任意两点距离之和

#include <bits/stdc++.h>

using namespace std;

typedef long long LL;
int const N = 5e2 + 10;

int n;
int d[N][N];
int p[N];
LL ans[N];
bool st[N];
int main() {
    cin >> n;
    for (int i = 1; i <= n; i++)
        for (int j = 1; j <= n; j++) cin >> d[i][j];

    for (int i = 1; i <= n; i++) cin >> p[i];

    for (int u = n; u; u--) {
        int k = p[u];
        st[k] = true;
        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                d[i][j] = min(d[i][j], d[i][k] + d[k][j]);

        for (int i = 1; i <= n; i++)
            for (int j = 1; j <= n; j++)
                if (st[i] && st[j]) ans[u] += d[i][j];
    }
    for (int i = 1; i <= n; i++) cout << ans[i] << " ";
    return 0;
}