C++ 算法竞赛、04 周赛篇 | AcWing 第5场周赛

AcWing 第5场周赛

竞赛 - AcWing

3726 调整数组

3726. 调整数组 - AcWing题库

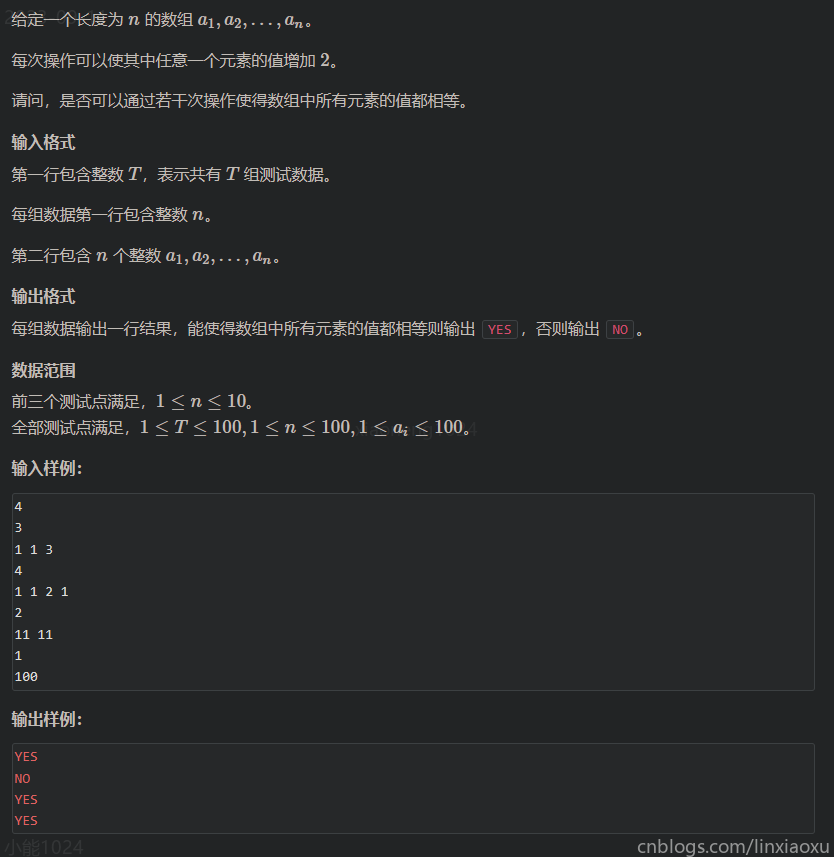
简单题，判断奇偶数是否同时存在

#include <bits/stdc++.h>

using namespace std;

int t, m;

int main() {
    cin >> t;
    while (t--) {
        cin >> m;
        bool f1 = false, f2 = false;
        for (int i = 0; i < m; i++) {
            int x;
            cin >> x;
            if (x & 1)
                f1 = true;
            else
                f2 = true;
        }
        if (f1 == f2)
            puts("NO");
        else
            puts("YES");
    }
    return 0;
}

3727⭐乘方相加

3727. 乘方相加 - AcWing题库

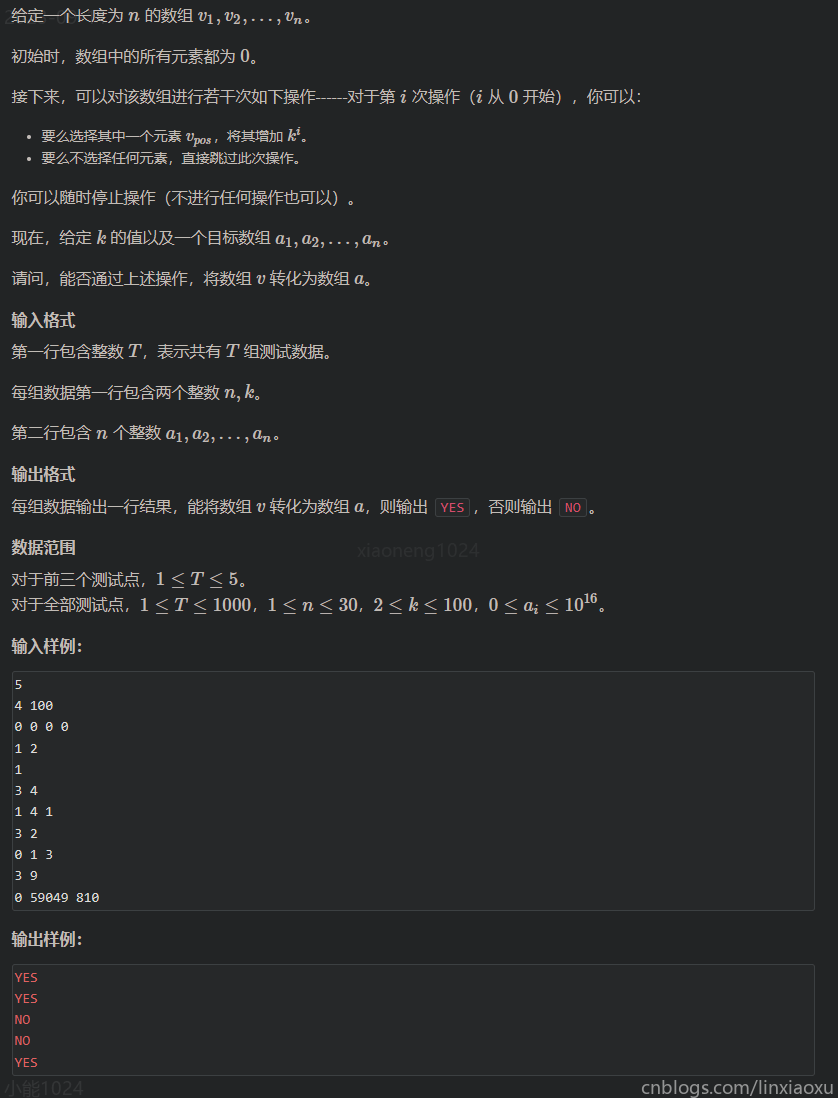
记录每个数据的 k 进制各个位数的值保存到数组，题目要求每位最多为 1，超过 1 则无法达到

#include <bits/stdc++.h>

using namespace std;

int const N = 1e2;
int t, m, k;
int s[N];

int main() {
    cin >> t;
    while (t--) {
        cin >> m >> k;
        memset(s, 0, sizeof s);  // 每组测试点初始化
        for (int i = 0; i < m; i++) {
            long long x;
            cin >> x;
            for (int j = 0; x; j++, x /= k) {
                s[j] += x % k;
            }
        }
        bool flag = true;
        for (int i = 0; i < N; i++) {
            if (s[i] > 1) flag = false;
        }

        if (flag)
            puts("YES");
        else
            puts("NO");
    }

    return 0;
}

3728⭐城市通电

3728. 城市通电 - AcWing题库

图是稠密图，用朴素版Prim求，\(O(n^2)\)

每点建立发电站的费用转化成：有一个超级原点，每个城市点连向超级原点的边的距离就是建立发电站的费用，如果该点连向该边，就是建立了发电站

用两个 Vector 分别存建立发电站的点 和 接电线的点，distp 用于获取每个点连向连通块的哪个点

#include <bits/stdc++.h>
#define y second
#define x first

using namespace std;

typedef long long LL;
typedef pair<int, int> PII;

int const N = 2e3 + 10;
PII q[N];
int c[N], k[N];
LL dist[N], distp[N];  // distp是每个点连向连通块的边对应的是连通块哪个点
bool st[N];
vector<int> ans1;  // 存建发电站
vector<PII> ans2;  // 存村庄和村庄之间的边
int n;

inline LL get_dist(int a, int b) {
    int dx = q[a].x - q[b].x;
    int dy = q[a].y - q[b].y;
    return (LL)(abs(dx) + abs(dy)) * (k[a] + k[b]);
}

LL prim() {
    // memset(dist, 0x3f, sizeof dist);
    LL res = 0;
    dist[0] = 0, st[0] = true;
    for (int i = 1; i <= n; i++) dist[i] = c[i];
    for (int i = 0; i < n; i++) {
        int t = -1;
        for (int j = 1; j <= n; j++)
            if (!st[j] && (t == -1 || dist[t] > dist[j])) t = j;
        st[t] = true;
        res += dist[t];
        if (!distp[t])
            ans1.push_back(t);
        else
            ans2.push_back({distp[t], t});
        for (int j = 1; j <= n; j++)
            if (!st[j] && dist[j] > get_dist(t, j)) {
                dist[j] = get_dist(t, j);
                distp[j] = t;
            }
    }
    return res;
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) cin >> q[i].x >> q[i].y;
    for (int i = 1; i <= n; i++) cin >> c[i];
    for (int i = 1; i <= n; i++) cin >> k[i];

    LL res = prim();
    cout << res << endl;
    cout << ans1.size() << endl;
    for (auto x : ans1) cout << x << " ";
    cout << endl;
    cout << ans2.size() << endl;
    for (auto &t : ans2) cout << t.x << " " << t.y << endl;

    return 0;
}