DS博客作业04--图
0.PTA得分截图

1.本周学习总结(0-5分)
1.1 总结图内容
图存储结构
比较常见和重要的图的存储结构:邻接矩阵和邻接表。
邻接矩阵:
内容:
邻接矩阵,顾名思义,是一个矩阵,一个存储着边的信息的矩阵,而顶点则用矩阵的下标表示。对于一个邻接矩阵M,如果M(i,j)=1,则说明顶点i和顶点j之间存在一条边,对于无向图而言,M(i,j)=M(j,i),所以其邻接矩阵是一个对称的矩阵;对于有向图而言,则未必是一个对称的矩阵。邻接矩阵的对角线元素都为0.如下图是一个无向图与其对应的邻接矩阵:
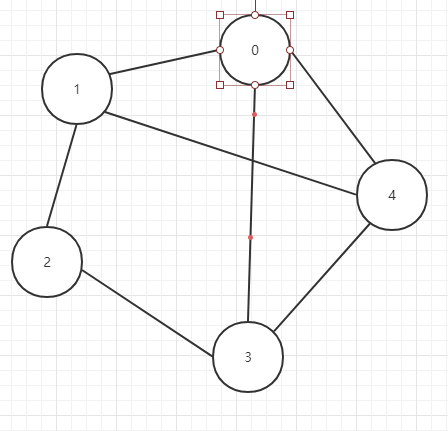
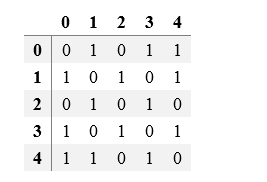
注意点:
图的邻接矩阵存储方式,结构由顶点数量、边数量、顶点集合和边集合组成。
其中顶点集合一维数组,根据顶点的数量动态分配数组大小。
边集合是二维数组,根据顶点的数量来动态分配数组大小,对于无向图来说,该邻接矩阵是对称矩阵。
邻接矩阵比较适用于稠密图。
结构体定义:
#define MAXV <最大顶点个数>
typedef struct
{ int no; //顶点编号
InfoType info; //顶点其他信息
} VertexType;
typedef struct //图的定义
{ int edges[MAXV][MAXV]; //邻接矩阵
int n,e; //顶点数,边数
VertexType vexs[MAXV]; //存放顶点信息
} MatGraph;
MatGraph g;//声明邻接矩阵存储的图
应用:
6-1 jmu-ds-邻接矩阵实现图的操作集
邻接表:
对于顶点数很多但是边数很少的图来说,用邻接矩阵显得略为“奢侈”,因为矩阵元素为1的很少,即其中的有用信息很少,但却占了很大的空间。所以邻接表的存在就很有必要了。
内容:
邻接表,存储方法跟树的孩子链表示法相类似,是一种顺序分配和链式分配相结合的存储结构。如这个表头结点所对应的顶点存在相邻顶点,则把相邻顶点依次存放于表头结点所指向的单向链表中。
对于无向图来说,使用邻接表进行存储也会出现数据冗余,表头结点A所指链表中存在一个指向C的表结点的同时,表头结点C所指链表也会存在一个指向A的表结点。
沿用上面邻接矩阵的无向图来构建邻接表,如下图所示:
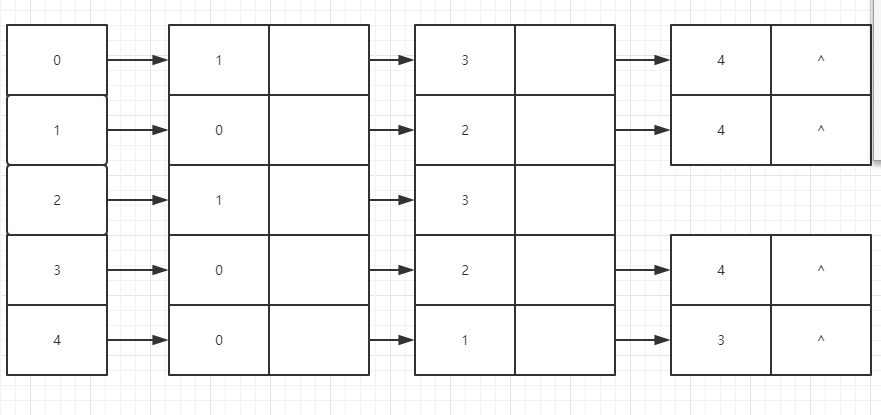
作为顶点0,它的邻接顶点有1,3,4,形成的边有(0,1),(0,3)和(0,4),所以顶点0将其指出来了;
对于顶点1,它的邻接顶点有0,2,4,所以顶点1将其指出来了,以此类推。
他们的边没有先后顺序之分。
左边的节点称为顶点节点,其结构体包含顶点元素和指向第一条边的指针;
右边的为边节点,结构体包含边的顶点对应的下标,和指向下一个边节点的指针。
对于有权值的网图,只需要在边节点增加一个权值的成员变量即可。
结构体定义:
typedef struct Vnode
{ Vertex data; //顶点信息
ArcNode *firstarc; //指向第一条边
} VNode;
typedef struct ANode
{ int adjvex; //该边的终点编号
struct ANode *nextarc; //指向下一条边的指针
InfoType info; //该边的权值等信息
} ArcNode;
typedef struct
{ VNode adjlist[MAXV] ; //邻接表
int n,e; //图中顶点数n和边数e
} AdjGraph;
AdjGraph *G;//声明一个邻接表存储的图G
应用:
6-2 jmu-ds-图邻接表操作
图遍历及应用。
图的遍历算法有两种:深度优先搜索和广度优先搜索
深度优先搜索:
内容:
深度优先搜索算法所遵循的策略是尽可能“深”地搜索一个图,它的基本思想是首先访问图中某一个起始定点v,然后由v出发,访问与v邻接且为被访问的任一个顶点w,再访问与w邻接且未被访问的任一顶点...重复上述过程,当不能再继续向下访问时,一次退回到最近被访问的顶点,若它还有邻接顶点未被访问,则从该点开始继续上述搜索过程,直到图中所有顶点均被访问过为止
算法实现:
void DFS(ALGraph *G,int v)
{ ArcNode *p;
visited[v]=1; //置已访问标记
printf("%d ",v);
p=G->adjlist[v].firstarc;
while (p!=NULL)
{
if (visited[p->adjvex]==0)
DFS(G,p->adjvex);
p=p->nextarc;
}
}
时间复杂度:
邻接表:O(n+e)
邻接矩阵:O(n2)
应用:
7-1 图着色问题
7-2 六度空间
判断图是否连通:
思想:
采用某种遍历方式来判断无向图G是否连通。先给visited[]数组(为全局变量)置初值0,然后从0顶点开始遍历该图。
在一次遍历之后,若所有顶点i的visited[i]均为1,则该图是连通的;否则不连通。
代码实现:
int visited[MAXV];
bool Connect(AdjGraph *G) //判断无向图G的连通性
{ int i;
bool flag=true;
for (i=0;i<G->n;i++) //visited数组置初值
visited[i]=0;
DFS(G,0); //调用前面的中DSF算法,从顶点0开始深度优先遍历
for (i=0;i<G->n;i++)
if (visited[i]==0)
{ flag=false;
break;
}
return flag;
}
应用:
7-5 通信网络设计 (10分)
查找图路径
如图
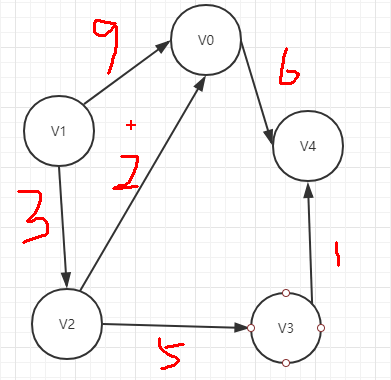
从图中的v1找到到v4的所有路径:
1.从v1出发,将v1标记,并将其入栈。
2.找到v0,将其标记,将其入栈。
3.找到v4,将其标记,入栈。v4是终点,将栈中的元素从栈底往栈顶输出,即为一条路径。v4出栈,并取消标记,回溯到v0。
4.v0除v4外无其它出度,将v0出栈,并取消标记,回溯到v1。
5.找到v2,将其标记并入栈。
6.找到v0,将其标记并入栈。
7.找到v4,将其标记,入栈。v4是终点,将栈中的元素从栈底往栈顶输出,即为一条路径。v4出栈,并取消标记,回溯到v0。
8.v0除v4外无其它出度,将v0出栈,并取消标记,回溯到v2。
9.找到v3,将其标记并入栈。
10.找到v4,将其标记,入栈。v4是终点,将栈中的元素从栈底往栈顶输出,即为一条路径。v4出栈,并取消标记,回溯到v3。
11.v3除v4外无其它出度,将v3出栈,并取消标记,回溯到v2。
12.v2除v0,v3外无其它出度,将v2出栈,并取消标记,回溯到v1。
13.v1除v0,v2外无其它出度,将v1出栈,栈空,结束遍历。
代码实现
void DFS(int start,int end)//深搜入栈查询所有路径
{
visited[start] = true;//visited数组存储各定点的遍历情况,true为已遍历(标记)
stack.Push(某个顶点);//入栈
for (int j = 0; j < list.Size(); j++) {
if (start== end) {//找到终点
for (int i=0; i < stack.Size()-1; i++) {
//输出从栈底到栈顶的元素,即为一条路径
}
stack.Pop();//出栈
visited[start] = false;
break;
}
if (!visited[j]) {//该顶点未被访问过
DFS(j,end);
}
if (j == list.Size() - 1 ) {//如果该顶点无其它出度
stack.Pop();
visited[start] = false;
}
}
}
广度优先搜索:
宽度优先搜索算法(又称广度优先搜索)是最简便的图的搜索算法之一,这一算法也是很多重要的图的算法的原型。Dijkstra单源最短路径算法和Prim最小生成树算法都采用了和宽度优先搜索类似的思想。其别名又叫BFS,属于一种盲目搜寻法,目的是系统地展开并检查图中的所有节点,以找寻结果。换句话说,它并不考虑结果的可能位置,彻底地搜索整张图,直到找到结果为止。
通俗来说,从某点开始,走四面可以走的路,然后在从这些路,在找可以走的路,直到最先找到符合条件的,这个运用需要用到队列。
代码实现:
邻接矩阵:
void BFS(AMGraph &G,char v0)
{
int u,i,v,w;
v = LocateVex(G,v0); //找到v0对应的下标
printf("%c ", v0); //打印v0
visited[v] = 1; //顶点v0已被访问
q.push(v0); //将v0入队
while (!q.empty())
{
u = q.front(); //将队头元素u出队,开始访问u的所有邻接点
v = LocateVex(G, u); //得到顶点u的对应下标
q.pop(); //将顶点u出队
for (i = 0; i < G.vexnum; i++)
{
w = G.vexs[i];
if (G.arcs[v][i] && !visited[i])//顶点u和w间有边,且顶点w未被访问
{
printf("%c ", w); //打印顶点w
q.push(w); //将顶点w入队
visited[i] = 1; //顶点w已被访问
}
}
}
}
邻接表:
void BFS(ALGraph &G, char v0)
{
int u,w,v;
ArcNode *p;
printf("%c ", v0); //打印顶点v0
v = LocateVex(G, v0); //找到v0对应的下标
visited[v] = 1; //顶点v0已被访问
q.push(v0); //将顶点v0入队
while (!q.empty())
{
u = q.front(); //将顶点元素u出队,开始访问u的所有邻接点
v = LocateVex(G, u); //得到顶点u的对应下标
q.pop(); //将顶点u出队
for (p = G.vertices[v].firstarc; p; p = p->nextarc) //遍历顶点u的邻接点
{
w = p->adjvex;
if (!visited[w]) //顶点p未被访问
{
printf("%c ", G.vertices[w].data); //打印顶点p
visited[w] = 1; //顶点p已被访问
q.push(G.vertices[w].data); //将顶点p入队
}
}
}
}
查找最短路径
有Dijkstra(迪杰斯特拉)算法和用Floyd(弗洛伊德)算法
Dijkstra(迪杰斯特拉)算法:
迪杰斯特拉(Dijkstra)算法主要是针对没有负值的有向图,求解其中的单一起点到其他顶点的最短路径算法。
算法思想:
设G=(V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的顶点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径 , 就将加入到集合S中,直到全部顶点都加入到S中,算法就结束了),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中,总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度。此外,每个顶点对应一个距离,S中的顶点的距离就是从v到此顶点的最短路径长度,U中的顶点的距离,是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。
具体操作
1.初始时,S只包含源点,即S={v},v的距离为0。U包含除v外的其他顶点,即:U={其余顶点},若v与U中顶点u有边,则<u,v>正常有权值,若u不是v的出边邻接点,则<u,v>权值为∞。
2.从U中选取一个距离v最小的顶点k,把k,加入S中(该选定的距离就是v到k的最短路径长度)。
3.以k为新考虑的中间点,修改U中各顶点的距离;若从源点v到顶点u的距离(经过顶点k)比原来距离(不经过顶点k)短,则修改顶点u的距离值,修改后的距离值的顶点k的距离加上边上的权。
4.重复步骤b和c直到所有顶点都包含在S中。
代码实现(仅仅只是思路,未进行测试)
const int MAXINT = 32767;
const int MAXNUM = 10;
int dist[MAXNUM];
int prev[MAXNUM];
int A[MAXUNM][MAXNUM];
void Dijkstra(int v0)
{
bool S[MAXNUM]; // 判断是否已存入该点到S集合中
int n=MAXNUM;
for(int i=1; i<=n; ++i)
{
dist[i] = A[v0][i];
S[i] = false; // 初始都未用过该点
if(dist[i] == MAXINT)
prev[i] = -1;
else
prev[i] = v0;
}
dist[v0] = 0;
S[v0] = true;
for(int i=2; i<=n; i++)
{
int mindist = MAXINT;
int u = v0; // 找出当前未使用的点j的dist[j]最小值
for(int j=1; j<=n; ++j)
if((!S[j]) && dist[j]<mindist)
{
u = j; // u保存当前邻接点中距离最小的点的号码
mindist = dist[j];
}
S[u] = true;
for(int j=1; j<=n; j++)
if((!S[j]) && A[u][j]<MAXINT)
{
if(dist[u] + A[u][j] < dist[j]) //在通过新加入的u点路径找到离v0点更短的路径
{
dist[j] = dist[u] + A[u][j]; //更新dist
prev[j] = u; //记录前驱顶点
}
}
}
}
Floyd(弗洛伊德)算法:
是解决任意两点间的最短路径的一种算法,可以正确处理有向图或负权的最短路径问题。时间复杂度为O(N3),空间复杂度为O(N2)。
算法思想:
从任意节点i到任意节点j的最短路径不外乎2种可能,1是直接从i到j,2是从i经过若干个节点k到j。所以,假设Dis(i,j)为节点u到节点v的最短路径的距离,对于每一个节点k,检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立,如果成立,证明从i到k再到j的路径比i直接到j的路径短,便设置Dis(i,j) = Dis(i,k) + Dis(k,j),这样一来,当遍历完所有节点k,Dis(i,j)中记录的便是i到j的最短路径的距离。
具体操作:
1.从任意一条单边路径开始。所有两点之间的距离是边的权,如果两点之间没有边相连,则权为无穷大。
2.对于每一对顶点 u 和 v,看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是更新它。
代码实现:
typedef struct
{
char vertex[VertexNum]; //顶点表
int edges[VertexNum][VertexNum]; //邻接矩阵,可看做边表
int n,e; //图中当前的顶点数和边数
}MGraph;
void Floyd(MGraph g)
{
int A[MAXV][MAXV];
int path[MAXV][MAXV];
int i,j,k,n=g.n;
for(i=0;i<n;i++)
for(j=0;j<n;j++)
{
A[i][j]=g.edges[i][j];
path[i][j]=-1;
}
for(k=0;k<n;k++)
{
for(i=0;i<n;i++)
for(j=0;j<n;j++)
if(A[i][j]>(A[i][k]+A[k][j]))
{ A[i][j]=A[i][k]+A[k][j];
path[i][j]=k;
}
}
}
应用:
7-6 旅游规划
6-4 jmu-ds-最短路径
最小生成树:
prim算法:
普里姆算法(Prim算法),图论中的一种算法,可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中,不但包括了连通图里的所有顶点,且其所有边的权值之和亦为最小。
具体操作:
输入:一个加权连通图,其中顶点集合为V,边集合为E;
初始化:Vnew = {x},其中x为集合V中的任一节点(起始点),Enew = {},为空;
重复下列操作,直到Vnew = V:
在集合E中选取权值最小的边<u, v>,其中u为集合Vnew中的元素,而v不在Vnew集合当中,并且v∈V(如果存在有多条满足前述条件即具有相同权值的边,则可任意选取其中之一);
将v加入集合Vnew中,将<u, v>边加入集合Enew中;
输出:使用集合Vnew和Enew来描述所得到的最小生成树。
代码实现:
void prim()
{
for (int i=1;i<=n;i++) //以1作为根节点
{
if(edge[1][i]!=INF)
p[i]=1;
d[i]=edge[1][i];
}
while (1)
{
int maxx=INF;
int u=-1;
for (int i=1;i<=n;i++) //找到距离生成树最短距离的节点
{
if(!vis[i]&&d[i]<maxx)
{
maxx=d[i];
u=i;
}
}
if(u==-1)
break;
vis[u]=1;
for (int i=1;i<=n;i++)
{
if(!vis[i]&&d[i]>edge[u][i])
{
d[i]=edge[u][i];
p[i]=u;
}
}
}
int sum=0;
for (int i=1;i<=n;i++)
if(p[i]==-1)
{
printf("不存在最小生成树\n");
return ;
}
else
sum+=d[i];
printf("最短生成树的长度为%d\n",sum);
return ;
}
时间复杂度:
邻接矩阵:O(n2)
邻接表:O(elog2n)
Kruskal算法
克鲁斯卡尔算法的基本思想是以边为主导地位,始终选择当前可用的最小边权的边。每次选择边权最小的边链接两个端点是kruskal的规则,并实时判断两个点之间有没有间接联通。
具体操作:
输入:图G
输出:图G的最小生成树
(1)将图G看做一个森林,每个顶点为一棵独立的树
(2)将所有的边加入集合S,即一开始S = E
(3)从S中拿出一条最短的边(u,v),如果(u,v)不在同一棵树内,则连接u,v合并这两棵树,同时将(u,v)加入生成树的边集E'
(4)重复(3)直到所有点属于同一棵树,边集E'就是一棵最小生成树
代码实现:
void Kruskal(AdjGraph *g)
{ int i,j,u1,v1,sn1,sn2,k;
int vset[MAXV]; //集合辅助数组
Edge E[MaxSize]; //存放所有边
k=0; //E数组的下标从0开始计
for (i=0;i<g.n;i++) //由g产生的边集E,邻接表
{ p=g->adjlist[i].firstarc;
while(p!=NULL)
{ E[k].u=i;E[k].v=p->adjvex;
E[k].w=p->weight;
k++; p=p->nextarc;
}
}
Sort(E,g.e); //用快排对E数组按权值递增排序
for (i=0;i<g.n;i++) //初始化集合
vset[i]=i;
}
应用:
7-4 公路村村通
拓扑排序:
介绍:
对一个有向无环图G进行拓扑排序,是将G中所有顶点排成一个线性序列,使得图中任意一对顶点u和v,若边(u,v)∈E(G),则u在线性序列中出现在v之前。一个AOV网应该是一个有向无环图,即不应该带有回路,因为若带有回路,则回路上的所有活动都无法进行(对于数据流来说就是死循环)。在AOV网中,若不存在回路,则所有活动可排列成一个线性序列,使得每个活动的所有前驱活动都排在该活动的前面,我们把此序列叫做拓扑序列,由AOV网构造拓扑序列的过程叫做拓扑排序。AOV网的拓扑序列不是唯一的,满足上述定义的任一线性序列都称作它的拓扑序列。
实现步骤:
在有向图中选一个没有前驱的顶点并且输出;
从图中删除该顶点和所有以它为尾的弧,即删除所有和它有关的边;
重复上述两步,直至所有顶点输出,或者当前图中不存在无前驱的顶点为止,后者代表我们的有向图是有环的,因此,也可以通过拓扑排序来判断一个图是否有环。
举例:
如下图:
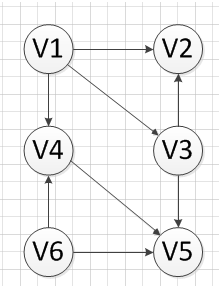
首先,我们发现V6和v1是没有前驱的,所以我们就随机选去一个输出,我们先输出V6,删除和V6有关的边,得到下图:
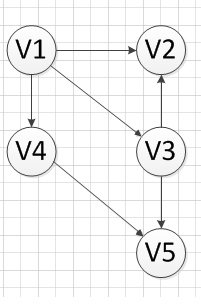
然后,我们继续寻找没有前驱的顶点,发现V1没有前驱,所以输出V1,删除和V1有关的边,得到下图:
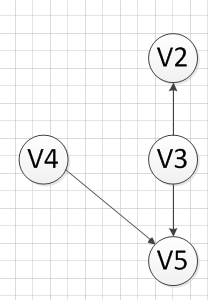
再然后,我们又发现V4和V3都是没有前驱的,那么我们就随机选取一个顶点输出,我们输出V4,得到下图:
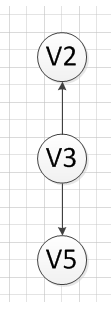
再再再然后,我们输出没有前驱的顶点V3,得:
没有然后了,最后我们分别输出V5和V2,最后全部顶点输出完成,
该图的一个拓扑序列为:v6–>v1—->v4—>v3—>v5—>v2。
结构体定义:
typedef struct //表头节点类型
{ vertex data; //顶点信息
int count; //存放顶点入度
ArcNode *firstarc; //指向第一条弧
} VNode;
代码实现:
void TopSort(AdjGraph *G) //拓扑排序算法
{ int i,j;
int St[MAXV],top=-1; //栈St的指针为top
ArcNode *p;
for (i=0;i<G->n;i++) //入度置初值0
G->adjlist[i].count=0;
for (i=0;i<G->n;i++) //求所有顶点的入度
{ p=G->adjlist[i].firstarc;
while (p!=NULL)
{ G->adjlist[p->adjvex].count++;
p=p->nextarc;
}
}
应用:
6-3 jmu-ds-拓扑排序 (20分)
关键路径:
介绍:
关键路径:AOE-网中,从起点到终点最长的路径的长度(长度指的是路径上边的权重和)。
假设起点是v0,则我们称从v0到vi的最长路径的长度为vi的最早发生时间,同时,vi的最早发生时间也是所有以vi为尾的弧所表示的活动的最早开始时间,使用e(i)表示活动ai最早发生时间,除此之外,我们还定义了一个活动最迟发生时间,使用l(i)表示,不推迟工期的最晚开工时间。我们把e(i)=l(i)的活动ai称为关键活动,因此,这个条件就是我们求一个AOE-网的关键路径的关键所在了。
具体步骤:
1.输入顶点数和边数,已经各个弧的信息建立图
2.从源点v1出发,令ve[0]=0;按照拓扑序列往前求各个顶点的ve。如果得到的拓扑序列个数小于网的顶点数n,说明我们建立的图有环,无关键路径,直接结束程序
3.从终点vn出发,令vl[n-1]=ve[n-1],按逆拓扑序列,往后求其他顶点vl值
4.根据各个顶点的ve和vl求每个弧的e(i)和l(i),如果满足e(i)=l(i),说明是关键活动。
1.2.谈谈你对图的认识及学习体会。
图的存储结构有两种,邻接矩阵和邻接表。邻接矩阵可以用二维数组来做,邻接表结构是好理解,但结构体的定义还是有一些复杂。
图是一种比线性表和树更为复杂的数据结构,在这种结构中,任意两个元素之间可能存在关系。
图的遍历分为深度遍历和广度遍历。算法上有Dljkstra算法,Floyd算法。
不知怎么的感觉最近学习总是有点赶,可能是最近学得比较理论化的东西且算法多而杂,有点迷糊。
2.阅读代码(0--5分)
2.1 题目及解题代码
题目:
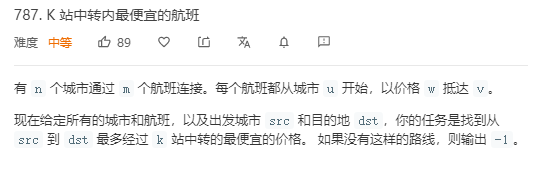
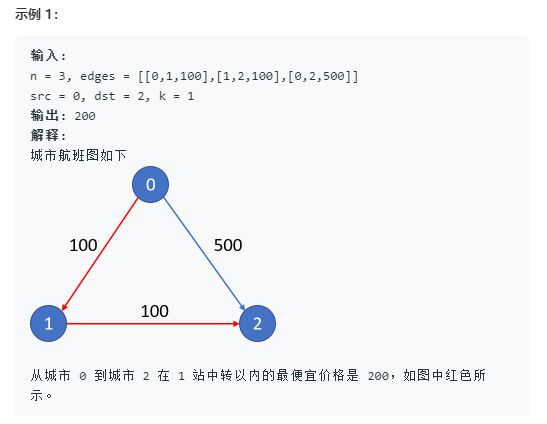
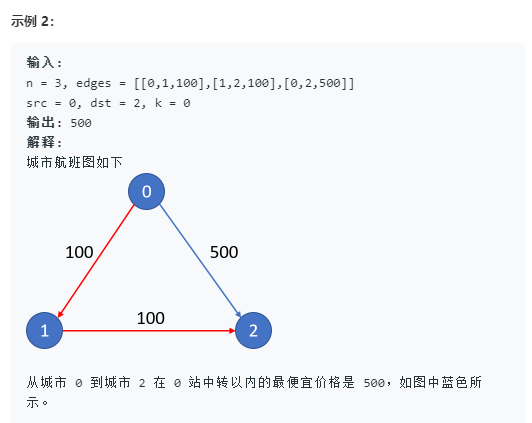
解题代码:
class Solution {
public:
int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) {
const int INF = 0x3f3f3f3f;
vector<int> dist(n, INF);
vector<int> backup(n);
dist[src] = 0;
for (int i = 0; i<= K; i++){
backup.assign(dist.begin(), dist.end());
for (auto &f: flights){
dist[f[1]] = min(dist[f[1]], backup[f[0]] + f[2]);
}
}
if (dist[dst] > INF /2) return -1;
return dist[dst];
}
};
2.1.1 该题的设计思路
本题用的是Bellman-Ford算法(似乎是一种高大上的算法,作者只说用了这个算法,没说这个算法怎么用,头大)
Bellman-Ford算法最关键的部分是松弛操作。即:
for i = 0 to i<= K
backup.assign(dist.begin(), dist.end());
for 枚举所有边
更新最短路
end for;
end for;
查了一下Bellman-Ford算法的应用:
处理有负权边的图;
循环次数的含义:循环K次后,表示不超过K条边的最短距离;
有边数限制的最短路;
如果有负权回路,最短路不一定存在;
Bellman-Ford算法可以求出是否有负环;
第n循环后,还有更新,说明路径上有n+1个点,也就是存在环,还有更新,说明环是负环;
循环n次后, 所有的边u->v,权w满足三角不等式:dist[v]<=dist[u]+w;
时间复杂度:O(n2);
空间复杂度:O(n2);
2.1.2 该题的伪代码
伪代码:
class Solution {
public:
int findCheapestPrice(int n, vector<vector<int>>& flights, int src, int dst, int K) {
const int INF = 0x3f3f3f3f;
定义vector<int> dist(n, INF)表示到起点的最短距离
定义vector<int> backup(n)为了防止串联
dist[src] = 0;
for i = 0 to i<= K
backup.assign(dist.begin(), dist.end());
for 枚举所有边
更新最短路
end for;
end for;
if (dist[dst] > INF /2) return -1;
return dist[dst];
}
};
2.1.3 运行结果
2.1.4分析该题目解题优势及难点。
优势点,同时也是难点:对Bellman-Ford算法的理解和使用,使代码量大大减少;
当然有个较大的缺点:复杂度高,运行效率略低。
2.2 题目及解题代码
题目:
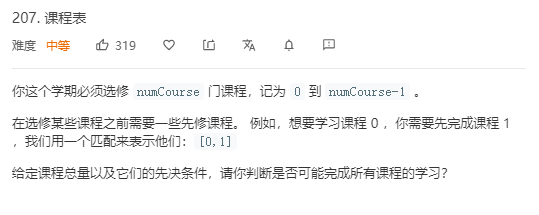


解题代码:
bool canFinish(int numCourses, vector<vector<int>>& prerequisites)
{
vector<int> inDegree(numCourses, 0);
vector<vector<int>> lst(numCourses, vector<int>());
for (auto v : prerequisites)
{
inDegree[v[0]]++;
lst[v[1]].push_back(v[0]);
}
queue<int> que;
for (auto i = 0; i < inDegree.size(); i++)
{
if (inDegree[i] == 0) que.push(i);
}
vector<int> ans;
while (!que.empty())
{
auto q = que.front();
que.pop();
ans.push_back(q);
for (auto l : lst[q])
{
if (--inDegree[l] == 0) que.push(l);
}
}
return ans.size() == numCourses;
}
2.2.1 该题的设计思路
本题应用拓扑排序,具体操作如下:
入度:设有向图中有一结点 v ,其入度即为当前所有从其他结点出发,终点为 v 的的边的数目。
出度:设有向图中有一结点 v ,其出度即为当前所有起点为 v ,指向其他结点的边的数目。
每次从入度为 0 的结点开始,加入队列。入度为 0 ,表示没有前置结点。
处理入度为 0 的结点,把这个结点指向的结点的入度 -1 。
再把新的入度为 0 的结点加入队列。
如果队列都处理完毕,但是和总结点数不符,说明有些结点形成环。
空间复杂度:O(N+e);
时间复杂度:O(N+e)。
2.2.2 该题的伪代码
bool canFinish(int numCourses, vector<vector<int>>& prerequisites)
{
遍历边缘列表,计算入度;
有向无环DAG图的存储,使用邻接表;
for (auto v : prerequisites)
初始化入度列表
初始化邻接表
end for;
queue<int> que;
for auto i = 0 to i < inDegree.size()
将入度为 0 的结点放入队列
end for;
vector<int> ans;
while (!que.empty())
将入度为0的进行出队;
ans.push_back(q);
for (auto l : lst[q])
if --inDegree[l] == 0
将入度=0的node进队,直到队列为空,且入度都为0了
end if;
end for;
end while;
return ans.size() == numCourses;
}
2.2.3 运行结果
2.2.4分析该题目解题优势及难点。
优势点同样也是难点:对拓扑排序的引用。拓扑排序的算法简洁程度比BFS和DFS要好,但是在时间和空间复杂度上比较糟糕。
2.3 题目及解题代码
题目:
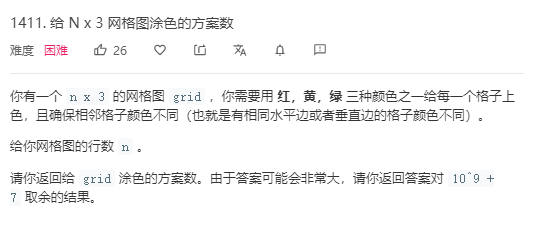



解题代码:
class Solution {
private:
static constexpr int mod = 1000000007;
public:
int numOfWays(int n) {
int fi0 = 6, fi1 = 6;
for (int i = 2; i <= n; ++i) {
int new_fi0 = (2LL * fi0 + 2LL * fi1) % mod;
int new_fi1 = (2LL * fi0 + 3LL * fi1) % mod;
fi0 = new_fi0;
fi1 = new_fi1;
}
return (fi0 + fi1) % mod;
}
};
2.3.1 该题的设计思路
本题,作者是应用数学公式来求符合该题条件的递推式;
经计算得到的递推式:
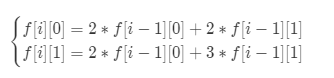
时间复杂度:O(N);
空间复杂度:O(1)。
2.3.2 该题的伪代码
class Solution {
private:
static constexpr int mod = 1000000007;
public:
int numOfWays(int n) {
int fi0 = 6, fi1 = 6;
for i = 2 to i <= n
带入递推式求解;
fi0 = new_fi0;
fi1 = new_fi1;
end for;
return (fi0 + fi1) % mod;
}
};
2.3.3 运行结果
2.3.4分析该题目解题优势及难点。
优势点,同样也是难点:应用数学知识求解递推式,大大降低了时间和空间复杂度,在代码精简度方面自然也是不言而喻。
与用普通的递推求解相比,该题解(强到爆炸!!!)
下面是普通递推求解:
class Solution {
private:
static constexpr int mod = 1000000007;
public:
int numOfWays(int n) {
vector<int> types;
for (int i = 0; i < 3; ++i) {
for (int j = 0; j < 3; ++j) {
for (int k = 0; k < 3; ++k) {
if (i != j && j != k) {
types.push_back(i * 9 + j * 3 + k);
}
}
}
}
int type_cnt = types.size();
vector<vector<int>> related(type_cnt, vector<int>(type_cnt));
for (int i = 0; i < type_cnt; ++i) {
int x1 = types[i] / 9, x2 = types[i] / 3 % 3, x3 = types[i] % 3;
for (int j = 0; j < type_cnt; ++j) {
int y1 = types[j] / 9, y2 = types[j] / 3 % 3, y3 = types[j] % 3;
if (x1 != y1 && x2 != y2 && x3 != y3) {
related[i][j] = 1;
}
}
}
vector<vector<int>> f(n + 1, vector<int>(type_cnt));
for (int i = 0; i < type_cnt; ++i) {
f[1][i] = 1;
}
for (int i = 2; i <= n; ++i) {
for (int j = 0; j < type_cnt; ++j) {
for (int k = 0; k < type_cnt; ++k) {
if (related[k][j]) {
f[i][j] += f[i - 1][k];
f[i][j] %= mod;
}
}
}
}
int ans = 0;
for (int i = 0; i < type_cnt; ++i) {
ans += f[n][i];
ans %= mod;
}
return ans;
}
};
时间复杂度:O(NT2);
空间复杂度:O(T2+TN)。



