DS博客作业02--栈和队列

0.PTA得分截图

1.本周学习总结（0-4分）

1.1 总结栈和队列内容

栈的定义：

栈（stack ）又称堆栈，它是运算受限的线性表。
其限制是仅允许在表的一端进行插入和删除操作，不允许在其他任何位置进行插入、查找、删除等操作。
表中进行插入、删除操作的一端称为 栈顶（top） ，栈顶保存的元素称为 栈顶元素。
相对的，表的另一端称为栈底（bottom） 
当栈中没有数据元素时称为空栈；
向一个栈插入元素又称为 进栈或 入栈；
从一个栈中删除元素又称为 出栈或 退栈。
由于栈的插入和删除操作仅在栈顶进行，后进栈的元素必定先出栈，
所以又把堆栈称为 后进先出表。

栈的存储结构:

顺序栈
和线性表类似，堆栈也有两种基本的存储结构：顺序存储结构和链式存储结构。
顺序栈是使用顺序存储结构实现的堆栈，即利用一组地址连续的存储单元依次存放堆栈中的数据元素。
由于堆栈是一种特殊的线性表，因此在线性表的顺序存储结构的基础上，选择线性表的一端作为栈顶即可。
根据数组操作的特性，选择数组下标大的一端，即线性表顺序存储的表尾来作为栈顶，此时入栈、出栈等操作可以在Ο(1)时间完成。
由于堆栈的操作都在栈顶完成，因此在顺序栈的实现中需要附设一个指针 top 来动态的指示栈顶元素在数组中的位置。
通常 top 可以用栈顶元素所在数组下标来表示，top= -1 时表示空栈。

栈的结构定义

typedef int SElemType;
typedef struct
{
    SElemType data[MAXSIZE];
    int top;//用于栈顶指针
}sqStack;

入栈操作：
Status Push(SqStack *s,SElemType e)
{
    if(栈满)
        return ERROR;
   栈顶指针加1；
   将新插入元素赋值给栈顶空间；
    return OK;
}

出栈操作：

status Pop(SqStack *s,SElemType *e)
{
    if(栈空)
        return ERROR;
    将要删除的栈顶元素赋值给e；
    栈顶指针减1；
    return OK;
}

链栈
链栈即采用链表作为存储结构实现的栈。
当采用单链表存储线性表后，根据单链表的操作特性选择单链表的头部作为栈顶，此时，入栈、出栈等操作可以在Ο(1)内完成。
由于堆栈的操作只在线性表的一端进行，在这里使用带头结点的单链表或不带头结点的单链表都可以。
使用带头结点的单链表时，结点的插入和删除都在头结点之后进行；
使用不带头结点的单链表时，结点的插入和删除都在链表的首结点上进行。

typedef struct StackNode
{
    SElemtype data;
    struct StackNode *next;
}StackNode,*LinkStack;
 
typedef struct LinkStack
{
    LinkStack top;
    int count;
}LinkStack;

入栈操作：
status Push(LinkStack *s,SElemType e)
{
    new一个s；
    s->data=e;
    把当前的栈顶元素赋值给结点的直接后继；
    将新的结点s赋值给栈顶指针；
    s->count++;
    return OK;
}

出栈操作：
status Pop(LinkStack *s,SElemType *e)
{
    LinkStack p;
    if(栈空)
    return ERROR;
    *e=s->top->data;
    将栈顶结点赋值给p；
    使得栈顶指针下移一位，指向后一结点；
    释放结点；
    s->count--;
    return OK;
}

栈的应用

1.平衡符号:

做一个空栈。读入字符直到文件尾。如果字符是一个开放字符，则将其推入栈中。
如果字符是一个封闭符号，则当栈空时报错；否则，将栈元素弹出。
如果弹出的符号不是对应的开放符号，则报错。
在文件尾，如果栈非空则报错。

具体例子：pta：7-3jmu-ds-符号配对和7-4符号配对

2.后缀表达式：

使用一个栈，当见到一个数时就把它推入栈中；
在遇到一个运算符时该运算符就作用于从该栈弹出的两个数上，将所得结果推入栈中。

例：
4.991。06+5.99+6.991.06=
转后缀表达式为：4.99 1.065.99+6.99 1.06+

3.中缀到后缀的转换：

从一个空栈开始计算，如果见到一个右括号，那么就将栈元素弹出，将弹出的符号写到直到遇到一个左括号，但是这个左括号只被弹出，并不输出。
如果见到任何其他的符号，那么从栈中弹出栈元素直到发现优先级更低的元素为止。【一个例外：除非是在处理一个“）”的时候，否则绝不从栈中移走“（”。对于这种操作，“+”的优先级更低，而“（”的优先级最高。当从栈弹出元素的工作完成后，再将操作符压入栈中。】
最后，如果读到输入的末尾，将栈元素弹出直到该栈变成空栈，将符号写到输出中。

例：pta：7-5 表达式转换

队列的存储结构及操作

队列：
队列是一种特殊的线性表，特殊之处在于它只允许在表的前端（front）进行删除操作，
而在表的后端（rear）进行插入操作，和栈一样，队列是一种操作受限制的线性表。
进行插入操作的端称为队尾，进行删除操作的端称为队头。队列中没有元素时，称为空队列。
链式队列是用单链表的形式来表示队列，但是要符合队列“尾进头出”的规则。

循环队列：

结构定义：
typedef int QElemtype;
typedef struct
{
    QElemtype data[MAXZIZE];
    int front;//头指针
    int rear;//尾指针，若队列不空，指向队尾元素的下一个位置
}Squeue;

初始化一个空队列：

ststus InitQueue(SqQueue *Q)
{
    Q->front=0;
    Q->rear=0;
    return OK;
}

循环队列求长度：

int QueueLength(SqQueue Q)
{
    return (Q.rear-Q.front+MAXSIZE)%MAXSIZE;
}

循环队列的入队操作：

statuas EnQueue(SqQueue *Q,QElemTYpe e)
{
    if(队列未满)
        return ERROR;
    将元素e赋值给队尾
    指针向后移动一位；
    return OK;
}

队列的链式存储结构与实现：

typedef int QElemType；
 
typedef struct QNode//结点结构
{
    QElemType data;
    struct QNode *next;
}QNode,*QueuePtr;
 
typedef struct//队列的链表结构
{
    QueuePtr front,rear;//队头，队尾指针
}LinkQueue;

插入元素e为Q的新的队尾元素：

status EnQueue(LinkQueue *Q,QElemtype e)
{
    new一个s；
    if(存储分配失败)
        exit(OVERFLOW);
    s->data=e;
    s->next=NULL;
    把拥有元素e新结点s赋值给原队尾结点的后继；
    把当前的s设置为队尾结点吗，rear指向s；
    return OK;
}

出队：

ststus DeQueue(LinkQueue *Q,QElemType *e)
{
    QueuePtr p;
    if(队空)
        return ERROR;
    将欲删除的队头结点暂时存给p;
    将欲删除的队头结点的值赋值给e;
    将原队头结点后继p->next赋值给头结点后继;
 
    if(队头是队尾)
    删除后将rear指向头结点;
    return OK;
}

队列应用

有几种使用队列来提高运行效率的算法。

1.2.谈谈你对栈和队列的认识及学习体会。

第三章主要介绍栈和队列的基本概念，存储结构，基本运算算法设计和应用实例。
从组成元素的逻辑关系来看，栈和队列都属于线性结构。
栈和队列与线性表的不同之处就在于他们的相关运算具有一些特殊性。
更准确地说，一般线性表上的插入、删除运算不受限制，而栈和队列上的插入、删除运算均受某种特殊限制，因此栈和队列也称为操作受限的线性表。
栈是一种常用而且重要的数据结构之一，如用到保存函数调用是所需要的信息，通常在将递归算法转换成非递归算法是需要使用到栈。

2.PTA实验作业（0-2分）

2.1.题目1：题目名称：6-5 jmu-ds-舞伴问题 (20分)

伪代码：

功能实现函数（其他省略）
定义person类型的e；
For（int i=0；i<num;i++）
完成男女分队；
While（男女队都非空）
输出男女；
End；

2.1.1代码截图

2.1.2本题PTA提交列表说明。

Q:格式错误
A:之前在线性表中放过这种错误，果断将题目的输出样例中姓名的间隔复制

2.2.题目2：题目名称：7-3 jmu-ds-符号配对 (15分)

伪代码：

用stack容器建栈st；
While（str【i】）
{
If（str【i】==‘（’||‘【’||‘{’）
入栈；
Else if（str【i】==‘）’||‘】’||‘}’）
{
If（st.empty（））
返回false；
取栈顶；
去栈顶；
Switch（str【i】）
如果不匹配右符号则将flag置为0；
i++;
}
if（栈空&&flag==1）
Return true；
Else
{
输出栈顶；
Return false；
}

2.2.2本题PTA提交列表说明。

Q：在vs中运行时出现奔溃的现象
A：忘记判断栈空的情况，加上判断语句

补充一题：7-8 电路布线 (20分)

代码：

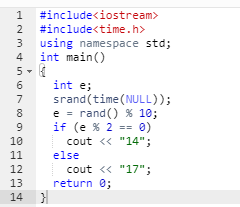
提交记录：

这题属于混分者的胜利！

3.阅读代码（0--4分）

3.1 题目及解题代码

题目：

7-9 彩虹瓶 (25分)
彩虹瓶的制作过程（并不）是这样的：先把一大批空瓶铺放在装填场地上，然后按照一定的顺序将每种颜色的小球均匀撒到这批瓶子里。
假设彩虹瓶里要按顺序装 N 种颜色的小球（不妨将顺序就编号为 1 到 N）。
现在工厂里有每种颜色的小球各一箱，工人需要一箱一箱地将小球从工厂里搬到装填场地。
如果搬来的这箱小球正好是可以装填的颜色，就直接拆箱装填；
如果不是，就把箱子先码放在一个临时货架上，码放的方法就是一箱一箱堆上去。
当一种颜色装填完以后，先看看货架顶端的一箱是不是下一个要装填的颜色，如果是就取下来装填，否则去工厂里再搬一箱过来。
如果工厂里发货的顺序比较好，工人就可以顺利地完成装填。
例如要按顺序装填 7 种颜色，工厂按照 7、6、1、3、2、5、4 这个顺序发货，
则工人先拿到 7、6 两种不能装填的颜色，将其按照 7 在下、6 在上的顺序堆在货架上；
拿到 1 时可以直接装填；拿到 3 时又得临时码放在 6 号颜色箱上；拿到 2 时可以直接装填；随后从货架顶取下 3 进行装填；
然后拿到 5，临时码放到 6 上面；最后取了 4 号颜色直接装填；剩下的工作就是顺序从货架上取下 5、6、7 依次装填。
但如果工厂按照 3、1、5、4、2、6、7 这个顺序发货，工人就必须要愤怒地折腾货架了，
因为装填完 2 号颜色以后，不把货架上的多个箱子搬下来就拿不到 3 号箱，就不可能顺利完成任务。
另外，货架的容量有限，如果要堆积的货物超过容量，工人也没办法顺利完成任务。
例如工厂按照 7、6、5、4、3、2、1 这个顺序发货，如果货架够高，能码放 6 只箱子，那还是可以顺利完工的；
但如果货架只能码放 5 只箱子，工人就又要愤怒了……
本题就请你判断一下，工厂的发货顺序能否让工人顺利完成任务。

输入格式：
输入首先在第一行给出 3 个正整数，分别是彩虹瓶的颜色数量 N（1<N≤10
​3
​​ ）、临时货架的容量 M（<N）、以及需要判断的发货顺序的数量 K。

随后 K 行，每行给出 N 个数字，是 1 到N 的一个排列，对应工厂的发货顺序。

一行中的数字都以空格分隔。

输出格式：
对每个发货顺序，如果工人可以愉快完工，就在一行中输出 YES；否则输出 NO。

输入样例：
7 5 3
7 6 1 3 2 5 4
3 1 5 4 2 6 7
7 6 5 4 3 2 1
    
输出样例：
YES
NO
NO

解题代码：

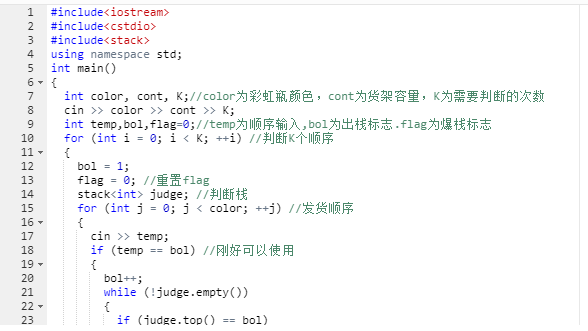
3.1.1 该题的设计思路

题意理解：
例如要按顺序装填 7 种颜色，工厂按照 7、6、1、3、2、5、4 这个顺序发货，则工人先拿到 7、6 两种不能装填的颜色，将其按照 7 在下、6 在上的顺序堆在货架上；拿到 1 时可以直接装填；拿到 3 时又得临时码放在 6 号颜色箱上；拿到 2 时可以直接装填；随后从货架顶取下 3 进行装填；然后拿到 5，临时码放到 6 上面；最后取了 4 号颜色直接装填；剩下的工作就是顺序从货架上取下 5、6、7 依次装填。
该段文字转图为：


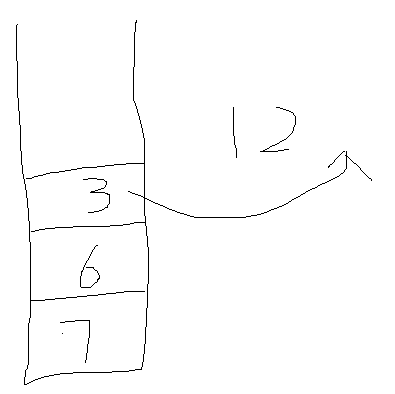
这种情况可顺利完成。

但如果工厂按照 3、1、5、4、2、6、7 这个顺序发货，工人就必须要愤怒地折腾货架了，因为装填完 2 号颜色以后，不把货架上的多个箱子搬下来就拿不到 3 号箱，就不可能顺利完成任务。
该段文字转图为：

因为3在栈底，所以该情况不可顺利完成。

另外，货架的容量有限，如果要堆积的货物超过容量，工人也没办法顺利完成任务。例如工厂按照 7、6、5、4、3、2、1 这个顺序发货，如果货架够高，能码放 6 只箱子，那还是可以顺利完工的；但如果货架只能码放 5 只箱子，工人就又要愤怒了……
该段文字转图为：

因为2无法入栈（栈过小），所以该情况不可顺利完成。

题目样例1：

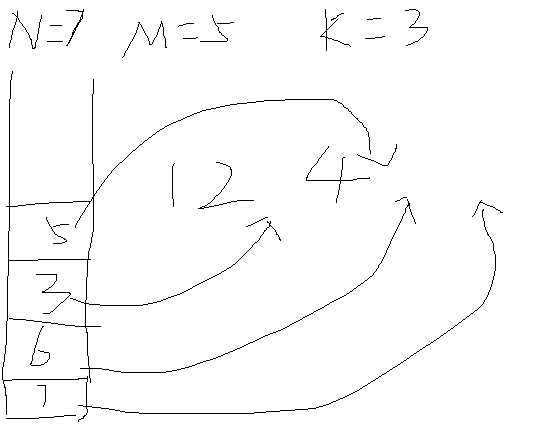
题目样例2：

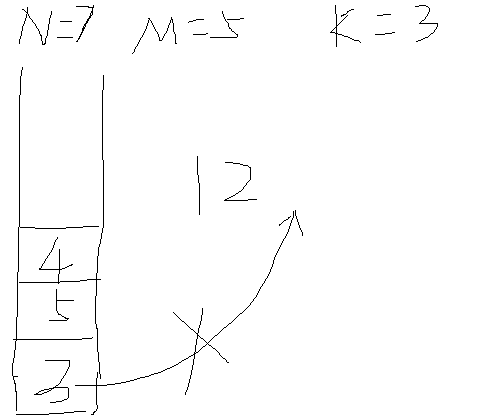
该情况属于文段2中的情况，3在栈底，无法顺利完成。

题目样例3：

该情况属于文段3中的情况，2无法进栈，无法顺利完成。

时间复杂度：O（n2）；
空间复杂度：O（1）。

3.1.2 该题的伪代码

int main()
{
	定义color为彩虹瓶颜色，cont为货架容量，K为需要判断的次数
	输入color，cont，K；
	定义temp为顺序输入,bol为出栈标志.flag为爆栈标志，初值为0；
	for (int i = 0; i < K; ++i) //判断K个顺序
	{
		for (int j = 0; j < color; ++j) //发货顺序
		{
		输入货物；
			if (刚好可以使用)
			{
				出栈；
				while (栈非空)
				{
					if (栈顶为需要货物)
					{
						出栈；
					}
					else break;
				}
			}
			else
			{
				入栈；
				flag置为1；
			}
		}
		if（不符合条件）
			输出NO；
		else
			输出YES；
	}
	return 0;
}

3.1.3 运行结果

3.1.4分析该题目解题优势及难点。

优势：
该题解很常规，选该题是觉得该题解可作为顺序栈复习时的典型例题；
难点：
文字的提取和分析部分，大多数人看到这么长的题目，头都大了（击溃学生的第一道防线就是超长的题目阅读）；
在设置flag（爆栈标志），在刚学栈时容易遗漏这个点（吃过亏）。

3.2 题目及解题代码

题目：

给定一个最大容量为 M 的堆栈，将 N 个数字按 1, 2, 3, ..., N 的顺序入栈，
允许按任何顺序出栈，则哪些数字序列是不可能得到的？
例如给定 M=5、N=7，则我们有可能得到{ 1, 2, 3, 4, 5, 6, 7 }，但不可能得到{ 3, 2, 1, 7, 5, 6, 4 }。

输入格式：
输入第一行给出 3 个不超过 1000 的正整数：M（堆栈最大容量）、N（入栈元素个数）、K（待检查的出栈序列个数）。
最后 K 行，每行给出 N 个数字的出栈序列。所有同行数字以空格间隔。

输出格式：
对每一行出栈序列，如果其的确是有可能得到的合法序列，就在一行中输出YES，否则输出NO。

输入样例：
5 7 5
1 2 3 4 5 6 7
3 2 1 7 5 6 4
7 6 5 4 3 2 1
5 6 4 3 7 2 1
1 7 6 5 4 3 2
          
输出样例：
YES
NO
NO
YES
NO

解题代码：

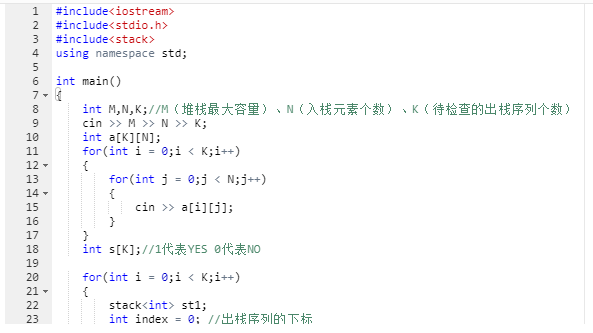
3.1.1 该题的设计思路

这个题就是给出栈的大小，然后按照1,2,3…n 顺序将数字入栈，允许按照任何方式出栈，来判断给出的出栈序列是否合法。
这个题可以分为三种情况来判断：
第一种就是，元素入栈之后立刻出栈，那么出栈序列的顺序还是1，2，…，n的顺序；
第二种情况就是前k个元素一直入栈，然后开始出栈，那么出栈序列的顺序就是k，k-1，……，1；
第三种情况就是前面这两种情况的结合。

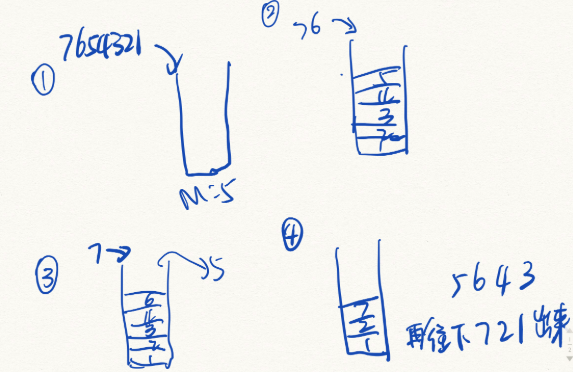
程序思路：
栈顶元素和出栈的序列号相比较，相同则pop,不同压入栈。
如果最后stack为空，则说明完全匹配了，那么就是合法序列，否则就是不合法序列。

时间复杂度：O（n2）；
空间复杂度O（n）。

3.2.2 该题的伪代码

int main()
{
	定义M为堆栈最大容量、N为入栈元素个数、K为待检查的出栈序列个数;
	输入M，N，K；
		定义数组a[K][N];
	for 读入数据;
	定义数组s[K];//用于判别，作用与flag相似
	for (i = 0; i < K; i++)
	{
		for (j = 1; j <= N; j++)
		{
			if (栈大小比M小)
			{
				入栈;
			}
			else
				break;
			while (栈非空)
			{
				if (栈顶与相应数组不等)
					跳出循环;
				else
				{
					出栈;
					continue;
				}
			}
		}
		if (栈空)
			s[i] = 1;
		else
			s[i] = 0;
	}
	for (i = 0; i < K; i++)
	{
		判断；
			输出；
	}
}

3.1.3 运行结果

3.1.4分析该题目解题优势及难点。

优势：
应用一个数字s[K]作为判断标识符，相当于flag，但是比flag灵活得多。
难点：
栈顶元素和出栈的序列号相比较，这一步，思路清晰，但是代码不好表述。