DS博客作业02--线性表
0.PTA得分截图

1.本周学习总结(0-4分)
1.1 总结线性表内容
顺序表结构体定义
typedef struct{
int *data;
int length;
}SqList;
顺序表的创建
void CreateSqList(SqList &L)
{
int i,node,n;
cin>>n;
L->data=new int[n];//动态申请分配n个int内存空间
for(i=0;i<n;i++)
{
cin>>node;
L->data[i]=node; //可以用下标法表示元素。
}
L->length=n;
}
顺序表插入
void InsertSeqlist(SeqList *L, int x, int i)
{
int j;
if(L->length == Maxsize) printf("表已满");
if(i < 1 || i > L->length + 1) printf("位置错"); // 检查插入位置是否合法
for(j = L->length;j >= i;j--)
{
L->data[j] = L->data[j - 1]; // 整体依次向后移动
}
L->data[i - 1] = x;
L->length++;
}
删除的代码操作
void DeleteSeqList(SeqList *L, int i)
{
int j;
if(i < 1 || i > L->length) printf("非法位置\n");
for(j = i;j < L->length;j++)
{
L->data[j - 1] = L->data[j]; // 依次左移
}
L->length--;
}
链表结构体定义
typedef struct Node
{
ElemType data;
struct Node *next;
}Node,*LinkList;
头插法
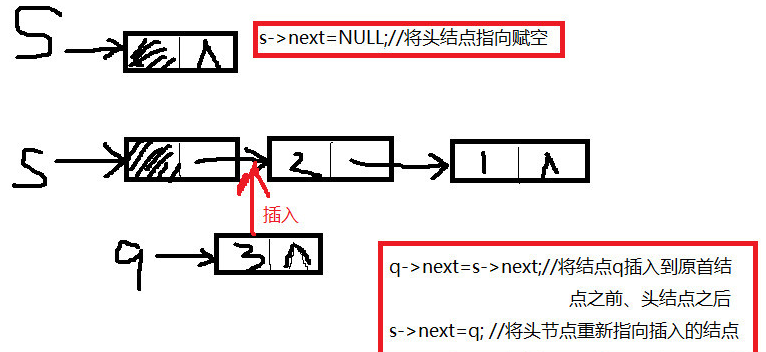
void CreateListF(LinkList& L, int n)//头插法建链表,L表示带头结点链表,n表示数据元素个数
{
LinkList s;
int i;
L = new LNode;
L->next = NULL;
for (i = 0; i < n; i++)
{
s = new LNode;
cin >> s->data;
s->next = L->next;
L->next = s;
}
}
尾插法
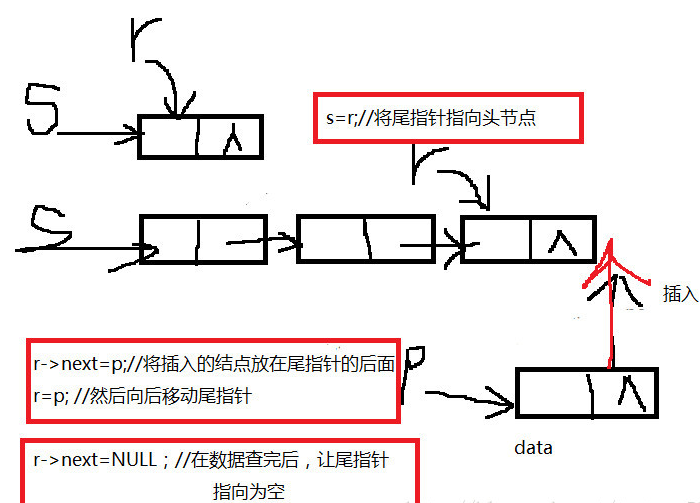
void CreateListR(LinkList& L, int n)//尾插法建链表,L表示带头结点链表,n表示数据元素个数
{
LinkList s, tail;
int i;
L = new LNode;
L->next = NULL;
tail = L;
for (i = 0; i < n; i++)
{
s = new LNode;
cin >> s->data;
s->next = NULL;
tail->next = s;
tail = s;
}
}
链表插入
void InsertSq(SqList& L, int x)
{
for (int j = L->length; j > 0; j--)
{
if (x >= L->data[j - 1])
{
L->data[j] = x;
break;
}
L->data[j] = L->data[j - 1];
L->data[j - 1] = x;
}
L->length++;
}
删除操作
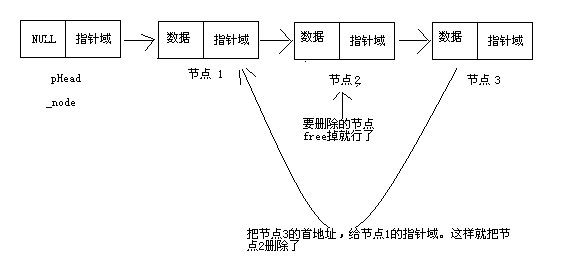
void DispSqList(SqList L)
{
int i = 0;
if (L->length != 0)
{
for (i = 0; i < L->length; i++)
{
cout << L->data[i];
if (i != L->length - 1)
cout << " ";
}
}
else
cout << "error";
}
有序表合并
void MergeList(LinkList& L1, LinkList L2)//合并链表
{
LinkList pa = L1->next, pb = L2->next, r, s;
r = L1;
while (pa != NULL && pb != NULL)
{
if (pa->data == pb->data)
{
if (pa->next != NULL)
pa = pa->next;
else
pb = pb->next;
}
if (pa->data < pb->data)
{
s = new LNode;
s->data = pa->data;
pa = pa->next;
r->next = s;
r = s;
}
else
{
s = new LNode;
s->data = pb->data;
pb = pb->next;
r->next = s;
r = s;
}
}
while (pa != NULL)
{
s = new LNode;
s->data = pa->data;
pa = pa->next;
r->next = s;
r = s;
}
while (pb != NULL)
{
s = new LNode;
s->data = pb->data;
pb = pb->next;
r->next = s;
r = s;
}
r->next = NULL;
}
循环链表结构特点
循环链表的特点是无须增加存储量,仅对表的链接方式稍作改变,即可使得表处理更加方便灵活。
【例】在链表上实现将两个线性表(a1,a2,…,an)和(b1,b2,…,bm)连接成一个线性表(a1,…,an,b1,…bm)的运算。
分析:若在单链表或头指针表示的单循环表上做这种链接操作,都需要遍历第一个链表,找到结点an,然后将结点b1链到an的后面,其执行时间是O(n)。
若在尾指针表示的单循环链表上实现,则只需修改指针,无须遍历,其执行时间是O(1)。
注意:
①循环链表中没有NULL指针。
涉及遍历操作时,其终止条件就不再是像非循环链表那样判别p或p->next是否为空,
而是判别它们是否等于某一指定指针,如头指针或尾指针等。
②在单链表中,从一已知结点出发,只能访问到该结点及其后续结点,无法找到该结点之前的其它结点。
而在单循环链表中,从任一结点出发都可访问到表中所有结点,这一优点使某些运算在单循环链表上易于实现。
双链表结构特点
①双链表也是线性表的一种。
单链表有两个存储单元:一个数据元素,一个后继结点。
单链表有一个弊端,就是要查找某个节点的先驱节点需要从头结点开始遍历,时间复杂度是O(n)。
双链表在单链表的基础上,增加了一个指向前驱节点的指针。
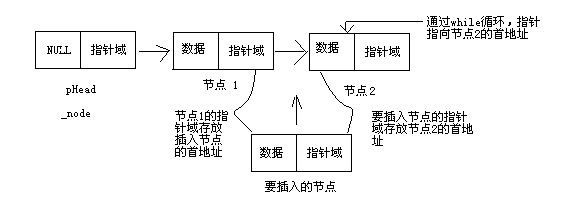
②单链表如果想要在指定节点之前插入元素,需要从头遍历找到指定节点的前驱节点,
然后将这个前驱节点的next指针指向添加的节点,将这个新添加的节点的next指针指向指定节点,时间复杂度是O(n)。
而双链表则不需要再遍历查找前驱节点,它有一个指向前驱节点的指针。
1.2.谈谈你对线性表的认识及学习体会。
本章线性表与上学期所学的链表接轨,所以前面有一部分是上学期学过的内容,学起来就相对容易。后面一部分是新的链表操作方法,
刚开始对链表的认识可能还不够深刻,所以总是会出现各种错误,后来错误减少了,但是发现自己的解题方法时间复杂度较高,总之
现在还在努力提高这一方面,准备多看看别人的代码让自己的代码更加好。
2.PTA实验作业(0-2分)
2.1.题目1:题目名称:6-8 jmu-ds-链表倒数第m个数
2.1.1代码截图

2.1.2本题PTA提交列表说明。
Q1:未从头结点开始遍历
A1:将j从0开始
Q2:一开始只判断了i-m是否大于0即m位置是否有效,并没有判断P是否等于NULL所以只有部分正确
A2:添加判断条件if(p!=NULL)
2.2.题目2:题目名称:6-1 jmu-ds-区间删除数据
2.2.1代码截图
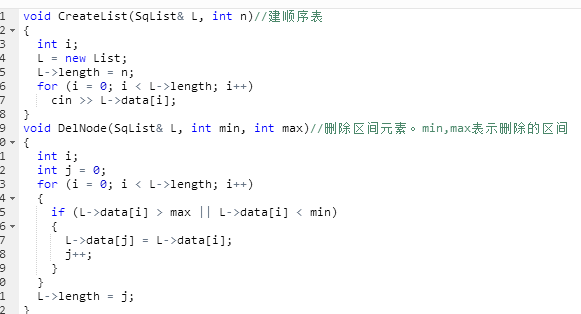

2.2.2本题PTA提交列表说明。
Q1:顺序表长度未改变
A1:定义j,用j来表示每次变化后的长度
Q2:“线性表为空!”这个文字(这个锅得由输入法来背)
A1:将“!”改为“!”(下次一定不手打,直接复制)
2.3.题目3:题目名称:6-10 jmu-ds-有序链表的插入删除
2.3.1代码截图

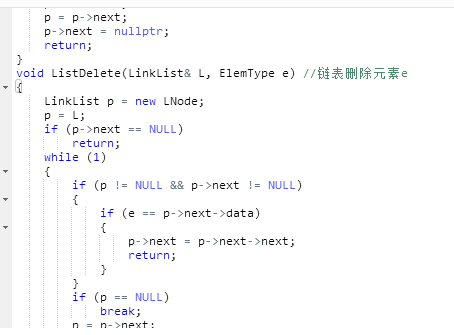
2.3.2本题PTA提交列表说明。
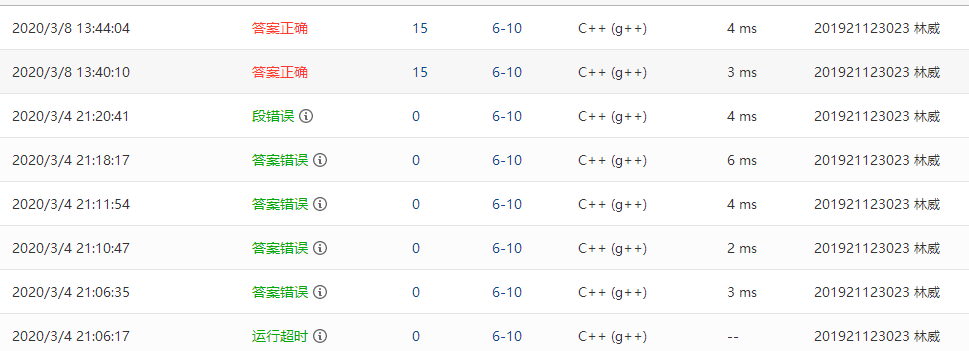
Q1:由于用循环但是忘记写跳出循环语句,陷入死循环
A1:添加break和return用于结束循环
Q2:在删除元素部分,尝试用delete结果多次错误
A2:放弃使用delete,当等e时,直接指向e的下一个,从而实现删除
3.阅读代码(0--4分)
3.1 题目及解题代码
题目:
代码:
struct ListNode* reverselist(struct ListNode* head)
{
//利用递归将链表逆置
if (head == NULL || head->next == NULL) return head;
struct ListNode* h = reverselist(head->next);
head->next->next = head;
head->next = NULL;
return h;
}
bool isPalindrome(struct ListNode* head)
{
if (head == NULL || head->next == NULL) return true;
struct ListNode* fast = head;
struct ListNode* slow = head;
while (fast && fast->next) //让慢指针走到链表中间位置
{
fast = fast->next->next;
slow = slow->next;
}
slow = reverselist(slow);//逆置后半部分的链表
while (slow)//比较前半部分的链表和后半部分的链表是否相同
{
if (slow->val != head->val)
{
return false;
}
slow = slow->next;
head = head->next;
}
return true;
}
3.1.1 该题的设计思路
使用两个指针,fast和slow指针。
(1)fast指针每次走两步,slow指针每次走一步;
(2)fast指针走到链表末尾的时候,slow指针走到链表的中间位置结点(链表长度n为偶数)或中间位置的前一个结点(链表长度n为奇数);
(3)slow直接到了中间,就可以将整个链表的后半部分压栈实现逆序,依次和前半部分比较

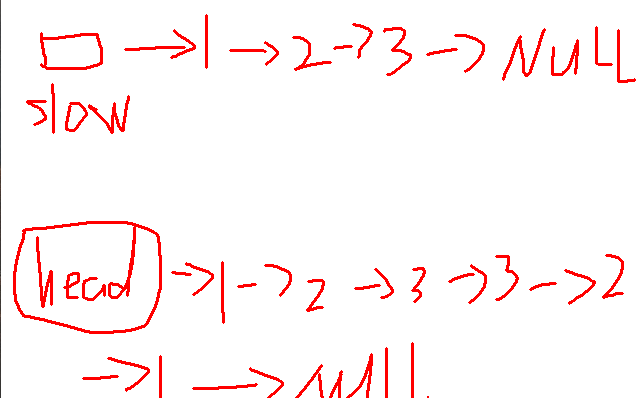
与链表的前半部分相比,若全部相同则是回文链表,否则不是
空间复杂度为O(n/2)
时间复杂度为O(n/2)
3.1.2 该题的伪代码
struct ListNode* reverselist(struct ListNode* head)
{
//利用递归将链表逆置
if (head 或者 head->next为空)
return head;
调用函数ListNode* h(指向head的下一个)
head->next->next = head;
head->next = NULL;
return h;
}
bool isPalindrome(struct ListNode* head)
{
if (head 或者 head->next为空)
return true;
定义快慢指针均指向head;
while (fast 和 fast->next不为NULL) //让慢指针走到链表中间位置
fast = fast->next->next;
slow = slow->next;
end while
逆置后半部分的链表
while (slow)
if (前半部分的链表和后半部分的链表不相同)
return false;
end while
return true;
}
3.1.3 运行结果

3.1.4分析该题目解题优势及难点。
优势及难点:
使用递归将链表逆置,使用快慢两个指针将时间复杂度减少n/2,大大提升效率。
使用快慢两个指针寻找中间节点和时间复杂度个人感觉是该题的难点。
3.2 题目及解题代码
题目:
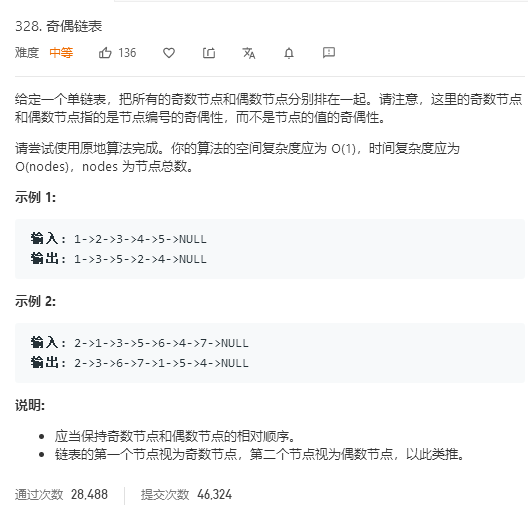
代码:
if (nullptr == head || nullptr == head->next || nullptr == head->next->next) return head;
ListNode* p = head, * temp = head, * secHead = head->next, * pre = nullptr;
int count = 0;
while (p) {
count++;
if (nullptr == p->next) break;
temp = p->next;
p->next = p->next->next;
pre = p;
p = temp;
}
if (count % 2 == 0)
pre->next = secHead;
else
p->next = secHead;
return head;
3.2.1 该题的设计思路
遍历链表,让每个节点都指向其下下个节点,这样就可以把奇偶链给分开,然后再把偶链连接到奇链上即可
空间复杂度为O(1)
时间复杂度为O(n)
3.2.2 该题的伪代码
if (head或head后两项均为空)
return head;
定义ListNode类型指针* p = head, * temp = head, * secHead = head->next, * pre = nullptr;
定义count,初值为0;//用于判断积偶
while (p)
count++;
if (nullptr == p->next) break;
temp = p->next;
p->next = p->next->next;
pre = p;
p = temp;
end while
if (count对2取余为0)//为偶
secHead则为pre的下一项;
else
secHead则为p的下一项;
return head;
3.2.3 运行结果
3.2.4分析该题目解题优势及难点。
优势:该题看了两种解法一种解法呢是用4个指针分别指向奇数链表的首尾节点和偶数链表的首尾节点,最后再把偶数链表和奇数链表连起来
另一种就是上述的解法,相对来说,这种解法比较浅显易懂,且在空间复杂度和时间复杂度上,效率更高
难点:count判断奇偶上,另一种解法未使用count在判断积偶上显得十分复杂(将偶数链表的尾部置空,奇数指向下一项)


