递归函数与二分法

def story():
    s = """
    从前有个山，山里有座庙，庙里老和尚讲故事，
    讲的什么呢？
    """
    print(s)
    story()
    
story()

递归的定义——在一个函数里再调用这个函数本身
现在我们已经大概知道刚刚讲的story函数做了什么，就是在一个函数里再调用这个函数本身，这种魔性的使用函数的方式就叫做递归。

递归的最大深度——997
正如你们刚刚看到的，递归函数如果不受到外力的阻止会一直执行下去。但是我们之前已经说过关于函数调用的问题，每一次函数调用都会产生一个属于它自己的名称空间，如果一直调用下去，就会造成名称空间占用太多内存的问题，于是python为了杜绝此类现象，强制的将递归层数控制在了997(只要997！你买不了吃亏，买不了上当...).

def story(n):
    s = """
    从前有个山，山里有座庙，庙里老和尚讲故事，
    讲的什么呢？
    """
    n += 1
    print(s)
    print(n)

    try:
        story(n)
    except RecursionError:
        print(n)
        exit()
		
story(1)

由此我们可以看出，未报错之前能看到的最大数字就是997.当然了，997是python为了我们程序的内存优化所设定的一个默认值，我们当然还可以通过一些手段去修改它：　

import sys
print(sys.setrecursionlimit(100000))
我们可以通过这种方式来修改递归的最大深度，刚刚我们将python允许的递归深度设置为了10w，至于实际可以达到的深度就取决于计算机的性能了

 

递归函数与三级菜单

menu = {
    '北京': {
        '海淀': {
            '五道口': {
                'soho': {},
                '网易': {},
                'google': {}
            },
            '中关村': {
                '爱奇艺': {},
                '汽车之家': {},
                'youku': {},
            },
            '上地': {
                '百度': {},
            },
        },
        '昌平': {
            '沙河': {
                '老男孩': {},
                '北航': {},
            },
            '天通苑': {},
            '回龙观': {},
        },
        '朝阳': {},
        '东城': {},
    },
    '上海': {
        '闵行': {
            "人民广场": {
                '炸鸡店': {}
            }
        },
        '闸北': {
            '火车战': {
                '携程': {}
            }
        },
        '浦东': {},
    },
    '山东': {},
}
def threeLM(dic):
    while True:
        for k in dic:print(k)
        key = input('input>>').strip()
        if key == 'b' or key == 'q':return key
        elif key in dic.keys() and dic[key]:
            ret = threeLM(dic[key])
            if ret == 'q': return 'q'

threeLM(menu)

　

二分查找算法

l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]
你观察这个列表，这是不是一个从小到大排序的有序列表呀？

如果这样，假如我要找的数比列表中间的数还大，是不是我直接在列表的后半边找就行了？

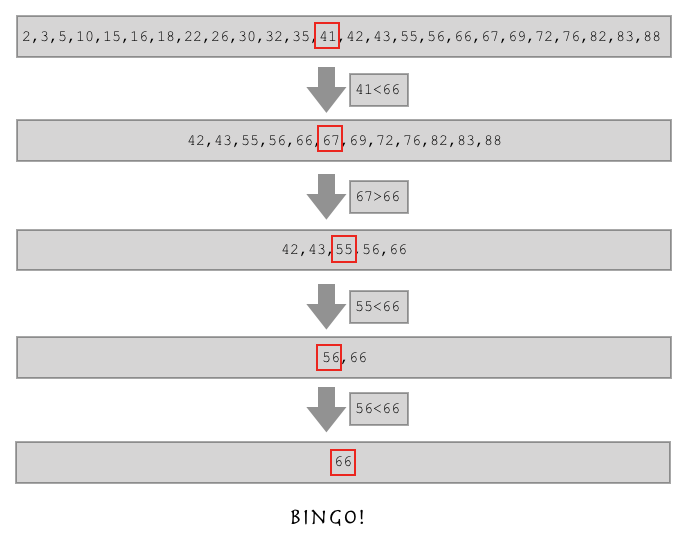
这就是二分查找算法！

那么落实到代码上我们应该怎么实现呢？

l = [2, 3, 5, 10, 15, 16, 18, 22, 26, 30, 32, 35, 41, 42, 43, 55, 56, 66, 67, 69, 72, 76, 82, 83, 88]
def func(l, aim,count):
    mid = (len(l) - 1) // 2

    if l:
        if aim > l[mid]:
            count += 1
            func(l[mid + 1:], aim, count)
        elif aim < l[mid]:
            count += 1
            func(l[:mid], aim,count)
        elif aim == l[mid]:
            count += 1
            print("找了%d次，才找到%d"%(count,aim))
    else:
        print('找不到')


func(l,66,0)#找了5次，才找到66

 

l = [2,3,5,10,15,16,18,22,26,30,32,35,41,42,43,55,56,66,67,69,72,76,82,83,88]

简单版二分法
def func(l,aim):
    mid = (len(l)-1)//2
    if l:
        if aim > l[mid]:
            func(l[mid+1:],aim)
        elif aim < l[mid]:
            func(l[:mid],aim)
        elif aim == l[mid]:
            print("bingo",mid)
    else:
        print('找不到')
func(l,66)
func(l,6)

升级版二分法
def search(num,l,start=0,end=0):
    start = start if start else 0
    end = end if end else len(l) - 1
    mid = (end - start)//2 + start
    if start > end:
        return None
    elif l[mid] > num :
        return search(num,l,start,mid-1)
    elif l[mid] < num:
        return search(num,l,mid+1,end)
    elif l[mid] == num:
        return mid

search(0,l)