关于float的小奥秘

一. float 存储方式

    1.1. float 占四个字节

    1.2. 浮点数构成

        1.2.1. 无论是单精度还是双精度在存储中都分为三个部分：

            <1>. 符号位(Sign) : 0代表正，1代表为负

            <2>. 指数位（Exponent）:用于存储科学计数法中的指数数据，并且采用移位存储(范围-127-128）

            <3>. 尾数部分（Mantissa）：尾数部分

                a. 其中float的存储方式如下图所示：

                b. 而双精度的存储方式为:

 

二. 浮点数计算方式

    2.1. 比如8.25用十进制的科学计数法表示就为:8.25*，而120.5可以表示为:1.205*,这些小学的知识就不用多说了吧。 

        但计算机只认识0，1，所以在计算机存储中，首先要将上面的数更改为二进制的科学计数法表示，8.25用二进制表示可表示为1000.01,（我靠，不会连这都不会转换吧?那我估计要没辙了。小数点左边表示,右边是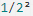）。120.5用二进制表示为：1110110.1用二进制的科学计数法表示1000.01可以表示为1.0001*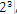,1110110.1可以表示为1.1101101*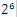,任何一个数都的科学计数法表示都为1.xxx*,尾数部分就可以表示为xxxx,第一位都是1嘛，干嘛还要表示呀？可以将小数点前面的1省略，所以23bit的尾数部分，可以表示的精度却变成了24bit，道理就是在这里，那24bit能精确到小数点后几位呢，我们知道9的二进制表示为1001，所以4bit能精确十进制中的1位小数点，24bit就能使float能精确到小数点后6位，而对于指数部分，因为指数可正可负，8位的指数位能表示的指数范围就应该为:-127-128了，所以指数部分的存储采用移位存储，存储的数据为元数据+127，下面就看看8.25和120.5在内存中真正的存储方式。

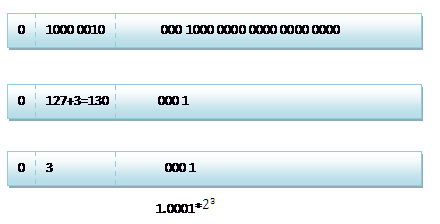
    2.2. 看下8.25，用二进制的科学计数法表示为:1.0001*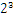

        2.2.1. 按照上面的存储方式，符号位为:0，表示为正，指数位为:3+127=130（至于为啥加127看后面） ,位数部分为,故8.25的存储方式如下图所示

 

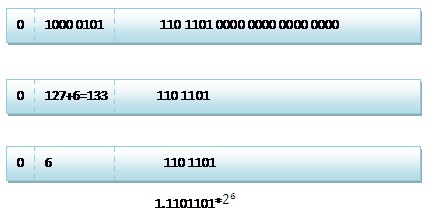
        2.2.2. 单精度浮点数120.5的存储方式如下图所示:

 

三. 为啥加127

   3.1. 

   

   3.1. 上面的例子中，我们知道E代表的是幂的大小，而存入计算机的e则为E+127，那么问题来了，这里为什么要加上127这个数呢？

        <1>. 

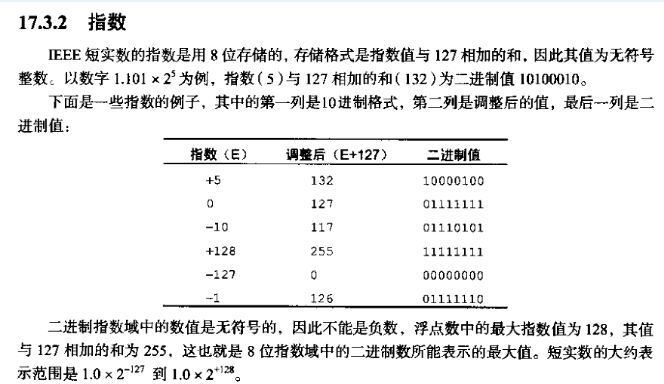
      <2>. 其实，也就是说：计算机表示单精度浮点数时，是用8位去存储指数部分，在数值上面，表示0~255，但是我们同样需要有负指数，正负指数的位数量为了均等，各自一半，-127~128，0是特殊点，特殊处理。储存时候会加上127，这样就刚刚好是0~255，就能很好的储存了，不然的话，需要判断符号位来判断数值的正负（计算机把指数拿去-127就可以得到正负）

 

面试题：

请写出float x 与“零值”比较的if语句

答案：

const float EPSINON = 0.00001；

if((x＞＝－EPSINON）＆＆（ｘ＜＝EPSINON））；