买卖股票的最佳实际问题
买卖股票的最佳时机问题
问题介绍
给定一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。在每一天,你可以决定是否购买和/或出售股票。你在任何时候最多只能持有一股股票。你也可以先购买,然后在同一天 出售。返回你能获得的最大利润。
解题思路
暴力法、贪心算法、动态规划法
暴力法
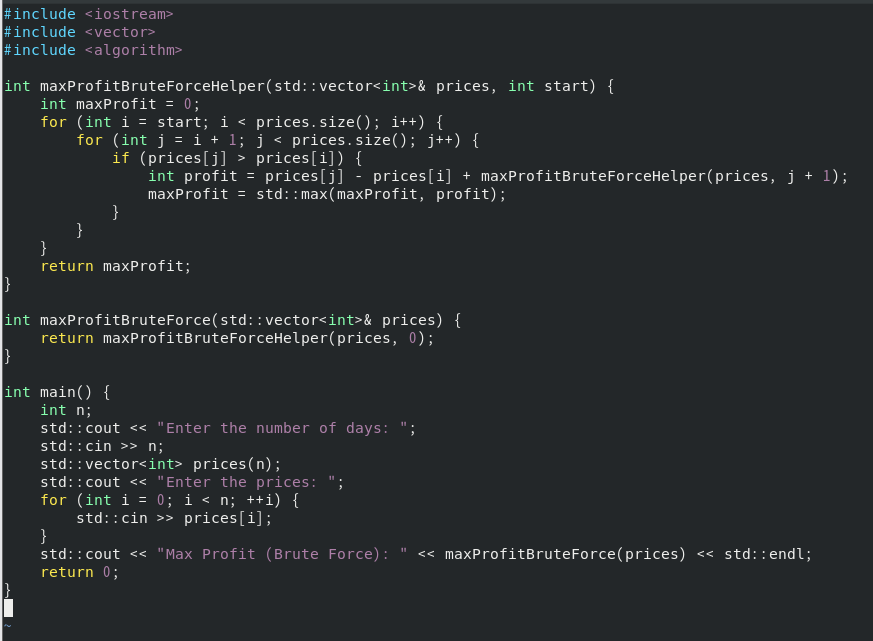
for (int i = start; i < prices.size(); i++) {
for (int j = i + 1; j < prices.size(); j++) {
外层循环从 start 开始,遍历 prices 向量,每次循环选择一个买入日 i。内层循环从买入日 i 的下一个元素开始遍历 prices,选择一个卖出日 j。
if (prices[j] > prices[i]) {
如果卖出日 j 的价格高于买入日 i 的价格,则计算利润。
int profit = prices[j] - prices[i] + maxProfitBruteForceHelper(prices, j + 1);
计算利润 profit,等于当前卖出价格减去买入价格,再加上从卖出日 j+1 之后可以获得的最大利润。通过递归调用 maxProfitBruteForceHelper 函数计算。
maxProfit = std::max(maxProfit, profit);
将当前计算的利润与之前的最大利润比较,取较大者作为新的最大利润。
贪心算法
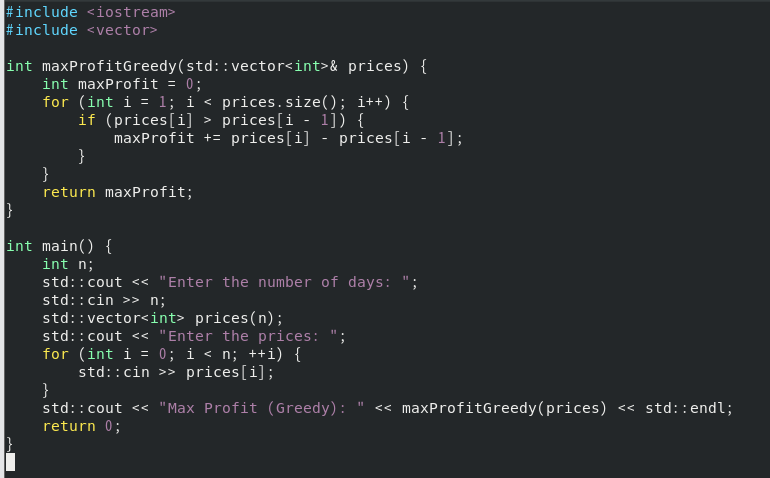
for (int i = 1; i < prices.size(); i++) {
if (prices[i] > prices[i - 1]) {
maxProfit += prices[i] - prices[i - 1];
}
}
从第2天开始,遍历 prices 向量。注意索引从1开始,这是因为我们需要比较相邻两天的价格。如果第 i 天的价格高于第 i-1 天的价格,就计算这两天的差价并加到 maxProfit 中。这个过程的核心思想是,只要今天的价格高于昨天的价格,就意味着可以买昨天的股票并在今天卖出赚取利润。
动态规划法
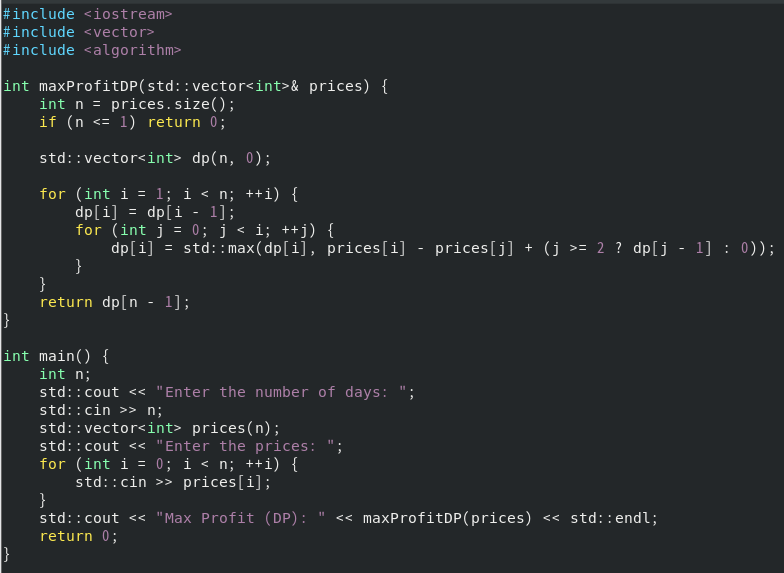
int maxProfitDP(std::vector<int>& prices) {
int n = prices.size();
if (n <= 1) return 0;
std::vector<int> dp(n, 0);
for (int i = 1; i < n; ++i) {
dp[i] = dp[i - 1];
for (int j = 0; j < i; ++j) {
dp[i] = std::max(dp[i], prices[i] - prices[j] + (j >= 2 ? dp[j - 1] : 0));
}
}
return dp[n - 1];
}
获取价格向量的大小 n。如果天数小于等于1,直接返回0,因为无法进行买卖。定义一个大小为 n 的动态规划数组 dp,并初始化为0。dp[i] 表示从第1天到第i天的最大利润。外层循环从第2天开始遍历价格向量。内层循环遍历从第1天到第i天的所有可能买入日 j。对于每一个 i,计算利润:prices[i] - prices[j] 表示第 i 天卖出和第 j 天买入的利润。如果 j >= 2,表示可以进行另一次交易,则再加上 dp[j - 1]。dp[i] = dp[i - 1] 确保当天不交易时的最大利润。dp[i] = std::max(dp[i], prices[i] - prices[j] + (j >= 2 ? dp[j - 1] : 0)) 更新 dp[i] 为较大的利润。
对比
算例一:
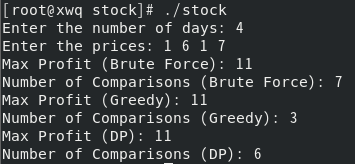
总天数:4
每天的股价:1、6、1、7
暴力法:
最大利润:11;关键操作计数:7
贪心算法:
最大利润:11;关键操作计数:3
动态规划法:
最大利润:11;关键操作计数:6
算例二:
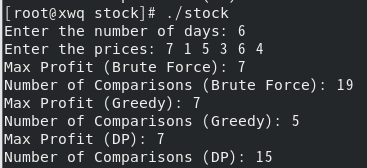
总天数:6
每天的股价:7、1、5、3、6、4
暴力法:
最大利润:7;关键操作计数:19
贪心算法:
最大利润:7;关键操作计数:5
动态规划法:
最大利润:7;关键操作计数:15
算例三:

总天数:10
每天的股价:100、180、260、310、40、535、695、140、360、220
暴力法:
最大利润:1085;关键操作计数:352
贪心算法:
最大利润:1085;关键操作计数:9
动态规划法:
最大利润:1085;关键操作计数:45
总结
暴力法 (Brute Force):
- 时间复杂度: O(n^2) 到 O(n!)
- 优点: 简单直接,易于理解和实现。
- 缺点: 由于需要遍历所有可能的买卖组合,时间复杂度很高,性能很差,尤其对于大规模数据集不适用。
贪心法 (Greedy):
- 时间复杂度: O(n)
- 优点: 高效,适用于大规模数据集。实现简单,只需一次遍历。
- 缺点: 只适用于某些特定情况下的问题,如每一天的价格上涨/下降趋势明显的情况。
动态规划 (Dynamic Programming):
- 时间复杂度: O(n^2)
- 优点: 能处理更多复杂情况,比暴力法更高效。可以记录并重用之前的计算结果,避免重复计算。
- 缺点: 依然比贪心法复杂,对某些特定情况不如贪心法高效。
根据以上三组测试样例的对比,可以发现贪心算法在处理该问题时会比暴力法和动态规划法更有优势,样本越大越能体现其优势。而动态规划法在一定程度上比起暴力法更加高效。
对于大多数实际应用场景,贪心法是效率最高的选择。不过,在一些复杂的情况下,动态规划可能会提供更灵活的解决方案。
#include <iostream>
#include <vector>
#include <algorithm>
// 声明全局计数器
int bruteForceComparisonCount = 0;
int greedyComparisonCount = 0;
int dpComparisonCount = 0;
// Brute Force Algorithm
int maxProfitBruteForceHelper(std::vector<int>& prices, int start) {
int maxProfit = 0;
for (int i = start; i < prices.size(); i++) {
for (int j = i + 1; j < prices.size(); j++) {
bruteForceComparisonCount++; // 每次进行比较时计数器加一
if (prices[j] > prices[i]) {
int profit = prices[j] - prices[i] + maxProfitBruteForceHelper(prices, j + 1);
maxProfit = std::max(maxProfit, profit);
}
}
}
return maxProfit;
}
int maxProfitBruteForce(std::vector<int>& prices) {
return maxProfitBruteForceHelper(prices, 0);
}
// Greedy Algorithm
int maxProfitGreedy(std::vector<int>& prices) {
int maxProfit = 0;
for (int i = 1; i < prices.size(); i++) {
greedyComparisonCount++;
if (prices[i] > prices[i - 1]) {
maxProfit += prices[i] - prices[i - 1];
}
}
return maxProfit;
}
// Dynamic Programming Algorithm
int maxProfitDP(std::vector<int>& prices) {
int n = prices.size();
if (n <= 1) return 0;
std::vector<int> dp(n, 0);
for (int i = 1; i < n; ++i) {
dp[i] = dp[i - 1];
for (int j = 0; j < i; ++j) {
dpComparisonCount++;
dp[i] = std::max(dp[i], prices[i] - prices[j] + (j >= 2 ? dp[j - 1] : 0));
}
}
return dp[n - 1];
}
int main() {
int n;
std::cout << "Enter the number of days: ";
std::cin >> n;
std::vector<int> prices(n);
std::cout << "Enter the prices: ";
for (int i = 0; i < n; ++i) {
std::cin >> prices[i];
}
// 调用并输出各算法结果和计数器值
std::cout << "Max Profit (Brute Force): " << maxProfitBruteForce(prices) << std::endl;
std::cout << "Number of Comparisons (Brute Force): " << bruteForceComparisonCount << std::endl;
std::cout << "Max Profit (Greedy): " << maxProfitGreedy(prices) << std::endl;
std::cout << "Number of Comparisons (Greedy): " << greedyComparisonCount << std::endl;
std::cout << "Max Profit (DP): " << maxProfitDP(prices) << std::endl;
std::cout << "Number of Comparisons (DP): " << dpComparisonCount << std::endl;
return 0;
}



