【算法笔记/数学内容】博弈论-从入土到入土

·前言

(update on 2022.1.12:回看的时候发现有些地方latex显示错误了……emm，把图修了一下）

由于我是傻逼，所以根本不会写博弈论，东西全是瞎搞的。

听完讲解外加搜了一堆博客之后弄出来的东西。

不懂的人珂以友链左转毛队博客qwq，她说过她写的东西大家都能康懂。

（大 声 哭 闹）

总而言之，博弈论就是一个特别庞大的东西，分了平等博弈和不平等博弈。平等博弈决策集等价，不平等博弈决策集不等价。

啊我也不知道该怎么写了。大概这个博客没有代码，只是纯粹记录一下思路。

(PS:因为我测试的时候好像有一些latex公式无法加载，但是刷新的时候貌似可以看到，如果实在看不到的话我补个图链）

 

·正文

1）ICG公平组合游戏

简而言之，就是两个人的行动方式是相同的，你来我往完美复制，反正不用改，也就是说决策集等价（是公（du）平（liu）的）

这个相信除了我之外都会，就不多说了。

 

2）SG函数

·SG游戏定义：无法操作者输

·SG函数定义：SG函数是对游戏图中每一个节点的评估函数。满足$SG(v) = mex\{SG(u) | 图中有一条从v到u的边\}$

·mex函数：返回不属于该集合的最小自然数，即$mex{S} = min(k | k \notin A \land k \in N)$

·SG函数的性质：

1、对于任意局面，如果它的SG值为0，那么它的任意后继SG值不为0

2、对于任意局面，如果它的SG值不为0，那么一定有一个后继状态的SG值为0

3、在SG游戏中，SG值为0时先手必败。

4、在每次只能进行一步操作的情况下，对于任何游戏的和，如果将其中任一单一SG-组合游戏换成数目为它SG值的一堆石子，则该单一SG-组合游戏的规则变为取石子游戏的规则(可以任意取)，则游戏的和的胜负不变。

5、若只考虑游戏的和，我们可以将其中任一游戏换成SG值相等的其他游戏，游戏的和的SG值不变。

这样子的话我们就可以把任意游戏的和转化为Nim博弈。

 

3）Nim博弈

正常版本：

给定n堆物品，第i堆物品有$a_{i}$个。

两名玩家轮流行动，每次可以任选一堆，取走任意多个物品，可把一堆取光，但不能不取

取走最后一件物品的人获胜。若两人都采取最佳策略，问能否获胜

解法：

相信大家都会，把所有的值异或起来，不为0就先手，为0就后手。

证明：

1、所有物品被取光肯定是必败状态

此时$a_{1} \bigoplus a_{2} \bigoplus a_{3} \bigoplus a_{4}... \bigoplus a_{n} = 0$

2、对于任意一个$a_{1} \bigoplus a_{2} \bigoplus a_{3} \bigoplus a_{4} ... \bigoplus a_{n} \neq 0$，那么假设这个数是x，它最高的1位是在k，那么必定存在一个$a_{i}$的第k位为1。

又因为此，所以$a_{i} \bigoplus k< a_{i}$。所以珂以把$a_{i}$变成$a_{i} \bigoplus x$。这样就可以给对手一个$a_{1} \bigoplus a_{2} \bigoplus a_{3} \bigoplus a_{4}... \bigoplus a_{n} = 0$的状态。

3、对于$a_{1} \bigoplus a_{2} \bigoplus a_{3} \bigoplus a_{4}... \bigoplus a_{n} = 0$的局面，两次操作后剩下的异或和肯定还是0。所以必败。

（这个不是我证得，纯属摘抄qwq）

变态版本：

给定n堆物品，第i堆物品有$a_{i}$个。

三名玩家轮流行动，每次可以任选一堆，取走任意多个物品，可把一堆取光，但不能不取

取走最后一件物品的人获胜。若三人都采取最佳策略，问谁能获胜

解法：

三进制xor，请。

答案为0直接判最后一个人，剩下的判能不能一步到C必胜局，暴力。

n个人的就再见吧qwq，这个可能只能暴力了qwq，但是思路应该是差不多的qwq

奇（du）奇（liu）怪（dao）怪（bao）的变种：

①阶梯博弈：

有亿些阶梯，地面表示第0号阶梯。每次都可以将一个阶梯上的石子向其左侧移动任意个石子，没有可以移动的空间时（即所有石子都位于地面时）输。

解法：

首先：阶梯博弈等效于奇数阶阶梯的Nim博弈。

将每两堆石子绑定在一起，若石子堆数为奇数，则将0位置与第1堆绑定在一起。而石子数可以是两堆间距离，可以是能够转移的数量等。
把所有奇数阶梯看成N堆石子做Nim。把石子从奇数堆移动到偶数堆可以理解为拿走石子。

②反Nim博弈：

开倒车反着来，拿走最后一个石子的人输。

解法：

一个状态为必胜态，当且仅当所有堆的石子个数为1，且

 

 

，或至少有一堆的石子个数大于1，且

 

 

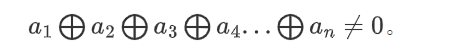
当所有堆石子数均为1时，胜负态与奇偶数相关（这个大家都知道qwq）

当仅有一堆石子数不为1时，先手总存在将其转化为前一种情况的必胜态的方案（这个大家也都会qwq）

当有多堆石子数不为1时，那就只能分类讨论了qwq

③Moore's Nimk：

两个人玩游戏，有n堆石子，每次操作可以选不超过k堆石子取任意多个，最少拿一颗，无子可取者为负。

解法：

k进制xor就完事了。

（这么一想好像和上面那个一堆人的有亿点点像，但是因为只有两个人所以说只要这么判就ok）

新Nim游戏：

在第一个回合中，第一个游戏者可以直接拿走若干个整堆的火柴。可以一堆都不拿，但不可以全部拿走。第二回合也一样，第二个游戏者也有这样一次机会。从第三个回合（又轮到第一个游戏者）开始，规则和Nim游戏一样。

解法：

拿走和最小的数字使得留下的数线性无关，即留下和最大的线性基，这样拿走的数量显然最少，找到和最大的线性基只需贪心的把数字从大到小加入到基中即可

 

4）其他的博弈类型

巴什博弈：

只有一堆n个物品，两个人轮流从这堆物品中取物， 规定每次至少取一个，最多取m个。最后取光者得胜

解法：

如果n能被m+1整除，那就后手赢，否则先手赢。这种问题一般都是周期性的。反正大力算周期就完了！！！

威佐夫博弈：

有两堆各若干个物品，两个人轮流从任一堆取至少一个或同时从两堆中取同样多的物品，规定每次至少取一个，多者不限，最后取光者得胜

解法：

我们将已经确定结果的局势称为奇异局势。保证$a[k]\leq b[k],k=0...n$且那么威佐夫博弈的前几个奇异局势是$（0，0）$,$（1，2）$,$（3，5）$,$（4，7）$...

找找规律，可以发现，第k个奇异局势的a[k]是前面的奇异局势中没有出现过的最小的数。而b[k]就是a[k]+k。

继续分析我们会发现，每种奇异局势的a[k]总是等于当前局势的差值乘上1.618

那么我们想到，0.618是黄金分割，即$\frac{\sqrt{5}-1}{2}$,那么我们把它转换到1.618，就可以得到$\frac{\sqrt{5}+1}{2}$

有一种比较通用的写法：

if a > b , 交换两个值。

　　c = b-a;

　　c = （int）(c*(（根号5）+1)/2）

　　if(c == b)  先手必输

　　else 先手必赢

那么就可以做完了。

 

5）博弈dp

整个方程然后直接打表找规律。好像也不大会写qwq

 

·总结&习题

写博弈论，最重要的几点就是要打表找规律。多数时候用这种方法就可以解决大多数问题。

题目贴一下：

·PE 306

·POJ2311 Cutting Game

·luoguP1290 欧几里德的游戏

·SDOI2009 E&D

·SPOJ COT3

·HDU6237 A simple stone game

·NOIP2010  三国游戏