recast navigation navmesh 导航网格 寻路算法 源码分析
recast navigation navmesh导航网格算法源码分析
Author: 林绍川
本文为了方便,引用了一些网上的相关图片
图片出处:Recast源码解析(二):NavMesh导航网格生成原理(上) - 程序员大本营 特此致谢
1 加载.obj文件
InputGeom::load--->InputGeom::loadMesh负责加载所有三角形
取obj文件中顶点数据,和顶点索引数据
1.1 obj的格式:
v 6.5 0.07999992 20.5
...(每行以v开头,连着三个浮点数,为一个顶点坐标)
f 1 2 3
...(每行以f开头,连着三个整数,为顶点索引)
1.2 三角形空间分割
rcCreateChunkyTriMesh,这个函数为之后建立高度场时,能快速索引出对应的三角形
按如下步骤:
1 此函数会为加载的三角形计算aabb盒(其实是xz坐标的包围矩形)
2 以aabb哪个轴长(x轴方向长),就按哪个轴进行排序,然按三角形数量1分为2
3 如此循环,直到划分的节点里三角形个数小于某个阀值(256)
2 建立高度场
结束加载obj,就要开始建立高度场
1 Recast navmesh是将场景中的三角形光栅光,形成高度场体素,
2 然后根据高度场计算layer,还生成导航多边形数据
为何不直接利用obj中的三角形数据,原因可能如下:
1 obj中的三角形数据可能细节更多,而导航寻路可以适当简化多边形细节,提高效率
2 寻路有对象宽度限制,体素化利于处理
3 obj中没有包含layer信息,需要处理
layer是recast navmesh里的一个概念,是导入obj里,一些独立,不连通的区域,或者不同的层,彼此之间寻路上不能互通,
或者通过port互通
此处以 Sample_TempObstacles::handleBuild为例,说明这一过程
这个sample支持动态创建障碍物,具体的处理方向如下步骤:
1 将高度场数据划分成tile,
2 障碍物改变与其相交的高度场体素,将处于障碍物(包围盒/或者圆柱体)中的体素标记为不可走
3 然后将受影响的tile重新计算,局部重新生成导航多边形数据
2.1 rasterizeTileLayers光栅化tile内三角形
光栅化场景中的三角形,即用一个正方形单元(xz平面),对场景中三角形数据进行采样高度数据,此处借用网上的一个图,形象表示如下:

图1
对图中的每个小方格,以下会以span这一称呼来代替,
一个span是xz大小固定的单元格,在y方向不固定
(根据光栅光时,截取到的多边形高范围,记录ymax ymin)
2.2 划分tile
Sample_TempObstacles为了动态重新开销减少,需要划分tile,
即将整个场景算出一个aabb,在xz平面上按固定大小分tile
每个tile内包含一个span体素数组
即tile是一个块, span则是一个最小的体素点,
二维的span组成一个tile
二维的tile组成一个场景
2.3 rasterizeTileLayers的参数 rcConfig
这个参数部分重要成员变量含义:
cs:
体素化的单位xz的量化(每个span在xz平面的长宽,为一个正方向)
ch:
y方向的量化单位
walkableSlopeAngle:
可攀爬的角度(0-90度),用来判断一个span是否可以行走(太斜了,就不能行走)
walkableHeight:
寻路单位的高度,高度不够,不能走, 例如:一个身高两米的人,不能通过只有1米高的门框之类的
walkableClimb:
同上,高度差小于此值,认为两个span是可以行走的
walkableHeight walkableClimb会被ch量化,例如:
ch=0.5 walkableHeight=2.0 那么 walkableHeight = walkableHeight / ch,
最终walkableHeight =4;
walkableRadius:
可行走的宽度,即一个太窄,狭小的地方认为不能走
walkableRadius会被cs量化
例如:
cs = 0.5 walkableRadius = 2.0
walkableRadius = walkableRadius / cs 即walkableRadius = 4
borderSize:
为每个tile多准备一些span数据,相当于边框,值会设成比walkableRadius大,避免把一些span错误置成不可行走
2.4 rcGetChunksOverlappingRect
此函数比较简单,计算当前tile范围,将tile包含的三角形找出来
2.5 rcMarkWalkableTriangles
依据walkableSlopeAngle,根据法线,判断哪些三角形不能走
2.6 rcRasterizeTriangles
对每个三角形调用rasterizeTri光栅化(或者说体素化),
形成一个高度场,(x,z)单元格,一个格子对应一个链表,链表里的数据按高度从小到大排列
2.7 rasterizeTri
对单个三角形进行光栅化(见图1)

在xz平面,对三角形进行分割,
循环调用dividePoly,先平行x轴模向切割, 再平行z轴纵切
2.7.1 dividePoly
分割多边形,以沿z轴平行分割为例,有如下 图2 图3两种情况
 图2
图2
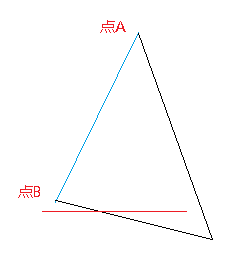 图3
图3
假设蓝色的那条边是要被分割的线,该函数会计算线段两个端点A,B的z坐标与分割线的z坐标差值
如果是图2的情况:
1 如果处理的点是A记入上半个多边形顶点,是B记入下半个
(根据d[i]的符号判断点是在A位置,还是在B位置)
2 交点分别计下上下两个多边形顶点
如果是图3的情况:
点A记入上半个多边形顶点(或者下半个多边形顶点,根据d[i]的符号)
代码片段,记算d[i]

体素化分割截取形象表示如下网图

三角形被x轴z轴的平行线切割后形成的多边形,取该多边形在y轴的最大值与最小值,生成span,
即上面所提到的图1,再次贴如下:

所对应的代码:

2.7.2 addSpan
这个函数会做一个处理,所有的span链表都是按高度从低到高排序的, span有多个邻居时,取高度最高的,
原因如下图:
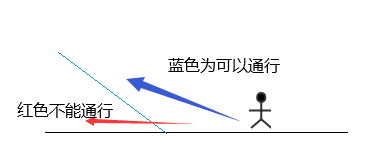
2.7.3 最终高度场
到此,完成了每个tile的高度场建立
参考网上找到的示意图,高度场形象表示如下:

每个span xz长度固定, y方向包含一个最大值最小值, 同一个xz坐标会有多个span,
同一个xz坐标处的所有span形成一个链表,并且按高度排序(从小到大)
2.7.4 rcFilterLowHangingWalkableObstacles
根据同一个xz坐标不同span之间,如果它们的距离不walkableClimb,并且下面的span可走,则把上面的span也标记成可走, 即处理台阶楼梯之类的情形
2.7.5 rcFilterLedgeSpans
和周围的span比较,"空洞"的高度差是否大于阀值,不大于阀值,说明不够高,
4个方向都不满足,该span也会被判断定为不能走,
例如:该span周围被墙包围,

如图所示的红线部分,rcFilterLedgeSpans这个函数,判断空洞交叠部分(红线长度)是否大开于路单位的高度walkableHeight
2.7.6 rcFilterWalkableLowHeightSpans
判断当前格子所形成的空间,是否足够高(>walkableHeight),不够高也判断为不可走
如下图所示,同一个xz坐标上,一系列的span,它们之间的高度差要足够

致此,完成了所有span能不能行走的标记
2.8 rcBuildCompactHeightfield
与周围的span进行比较,是否高度足够,并且高度差是可以走的,形成连接信息
即每个span会记录与周围前后左右四个邻是否连通
如果当前坐标为xz邻居方向dir值
0:表示x-1的span
1:表示z+1的span
2:表示x+1的span
3:表示z-1的span
Recast navmesh邻居定义图示如下:

2.9 rcErodeWalkableArea
Erode的中文含义为侵蚀,即将障碍物周围可行走区域按radius值适当扩散不可行走区域,目的是寻路目标贴墙走时,留出一定的宽度
在不可行走的区域周围,标记格子g(格子的邻居存在不可行走区域)
格子g与障碍的距离dis标记为0(dis默认为0xff)
继续处理,标记出所有格子与障碍物的距离,根据格子的可连通邻居dis值
根据dis值与寻路物体宽度值radius比较,小则将该区域也标记成不可行走
如下图所示,可行走区域要收缩一些,为寻路单位留出walkableRadius

2.10 rcMarkConvexPolyArea
这个是动态障碍用的,把一些span标记成不可行走
函数很简单,不影响对主要代码的理解,不详细说明了
2.11 rcBuildHeightfieldLayers
完成了高度场"扁平化",
每个layer
rcHeightfieldLayer::area: 保存是否可行走
rcHeightfieldLayer::heights:高度
rcHeightfieldLayer::cons:连通性(低4bit)+是否为layer之间的通道(高4bit)
以下说明该函数的执行过程:
2.11.1 找出连通区域
互相连接的span会形成一个区域,形成区域的规则如下图所示: (*每个代表一个span)

对应的部分代码片段截图

2.11.2 相邻的连通区域合并成一个区域
2.11.2.1 根据区域内span的邻居的区域id,为每个区域添加邻居
部分代码片段如下

2.11.2.2 同时根据span的链表,可以查当该span同一个xz坐标处的其它layer,记录下
形象图示如下

对应的代码片段

2.11.2.3 把所有互相连接的连通区域的打上同一个layerId, 排除掉自身的"不同层" 邻居的"不同层"
即:区域之间根据邻接关系互联的时候, 不同的层不能是同一个区域, 邻居的不同层也不能进入同一个区域
这样处理是为了扁平化高度场,区分出不同的层,
将3d的场景,转化成不同的层级的2d场
同时对于不连接的区域, 为了减少区域数量,对于高度差小于阀值的区域之间,也会进入合并处理
(不理解可以跳过此段代码处理,对整个逻辑理解不影响,是一个优化操作)
该优化部分代码片段如下:

2.11.2.4 扁平化的高度场数据保存
见2.11处
每个layer保存
rcHeightfieldLayer::area: 保存是否可行走
rcHeightfieldLayer::heights:高度
rcHeightfieldLayer::cons:连通性(低4bit)+是否为layer之间的通道(高4bit)
3 buildNavMeshTilesAt从压缩的高度场中,重建导航数据
大致过程如下:
1 扁平化高度场数据会被压缩,解压高度场数据
2 重建导航数据是逐个tile进行,
3 tile先按区域进行边缘检测,得到多边形
4 将多边形分解成三角形
5 将三角形进行适当合并(保证合并后的多边形是凸的)
6 记录tile多边形邻接信息
7 tile之间检测多边形边交叠情况,记录连接信息
下面进行详细说明
3.1 标记动态障碍
dtMarkCylinderArea
dtMarkBoxArea
dtMarkBoxArea
动态障碍物标记,改变与障碍物相交的area(可以理解为前文提到的span)标记为不可行走
对代码理解不影响,可以跳过
3.2 dtBuildTileCacheRegions 再次生成区域数据
部分逻辑参考 2.11 rcBuildHeightfieldLayers
1 将已经扁平化的高度场数据重新生成区域,
2 相信的区域组合成一个区域
原因:因为动态障碍支持,不能从解压后的数据直接取结果
canMerge函数比较难以理解,做个简要说明:
1 oldRegId邻居中有一个regId为newRegId,可以合并
2 count=0:表时newRegId并不在oldRegId邻居
3 count>=2:说明oldRegId已与别的区域合并,不能再newRegId合并,否则会导致合并好的区域又分裂了
4 这样处理,保证合并区域不断变大
可以自行画三个相邻的区域,按代码来理解canMerge的含义
因为数据已经扁平化,这里就没有扁平化处理了
3.3 dtBuildTileCacheContours 轮廓处理
dtTileCacheContour::verts:记录的轮廓 (即多边形的顶点)
dtTileCacheContour::reg:区域id
dtTileCacheContour::area可行走标识
多边形的点的顺时针记录的
以下进行详细说明
3.3.1 walkContour
遍历tile中所有xz坐标,
从每个合法的点area(即span)查找边缘
每个点与周围4个邻点,如果所处的reg不一样,则认为是边界点
4个邻点标号如下图所示,从3号位开始比对
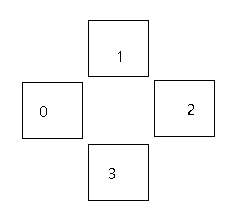

#表示其它区域的点 1.2.3.4表示当前要查找的轮廓边缘点, 如果出现x(或z)坐标相同的点,则会把中间的点舍弃
以上图为例从1点开始
1. 点1的三号位,即点1的下方提#所以点1是边缘点
2. 按代码逻辑,x,z不变,然后顺时针旋转,即dir=0,代码片段如下,可以看出当处理3号位时,只改变dir
 <代码片段1>
<代码片段1>
3. 此时判断点1与点2,发现它们是同一个区域的,发现它们是同一区域,此时会把dir逆时针转回去
即dir=0,同时x,z坐标变成点2,代码片段如下

4. 点2的下方是#,说明点2是边缘点,dir这时又顺时针转,即dir=0,同时x,z还是点2的,见<代码片段1>的逻辑
5. 点2的左边(dir=0)是不同区域,将z坐标加1(见<代码片段1>),到点3,同时dir=1,
因为左下角是不同区域点3也算边缘点
6. 点3的上方(dir=1)是同一个区域,把xz坐标切到点4,并逆时针处理dir=0
7. 点4的左边(dir=1)是同不区域,点4是边缘点
8. 就这样不断地旋,切坐标,把轮廓找出来,当回到点1 时,说明找到了完整的轮廓,判断代码如下
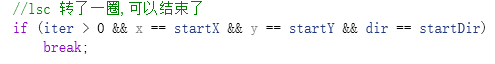
9. 可以看出点是按顺时针存储的
以下4图片形象说明了这一过程:




3.3.2 simplifyContour简化轮廓
将轮廓分段,如果该段内的点偏离段小于阀值,合并这些点
采用Douglas-Peucker算法
1 按顺序存储的一系列顶点,将首尾两点(记为V0和Vn)连成线段
2 计算中间各点与该线段的距离,如果距离小于某个阀值忽略,大于阀值的记录下来,这个点我们记录Vmaxd
3 Vmaxd与V0 Vn分别组成两条线段 V0-Vmaxd Vmaxd-Vn,分别对这两条线段重复第2步骤,
4 得到一系列线段,并且没有中间点与对应线段距离大于阀值,结束处理过程
形象图示如下: 此图出处 Douglas-Peucker算法 - qingsun_ny - 博客园

3.3.3 getCornerHeight
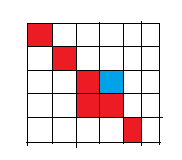
如图所示的蓝点,如果轮廓中有这样的占,要去除,是一种容错机制,
不好理解可以跳过,不影响后面的代码理解
3.3.4 工具函数介绍
distancePtSeg 计算点到线段的距离,根据向量点乘算出垂足坐标,再计算点与垂足的距离即可
代码片段截取如下:

3.4 dtBuildTileCachePolyMesh 生成邻接多边形
navmesh导航算法需要确保多边形是凸的,此函数负责生成凸多边形,并生成邻接信息
因为高度场已经扁平化,所以这个函数的操作都是在xz平面上行进的
1 先把之前得到的多边形轮廓(有可能是凹的),分割成三角形
2 再把三角形组合成多边形(确保是凸的)
3 处理多边形之间的邻接关系
以下详细说胆此函数
3.4.1 triangulate
将多边形(有可能是凹的)分割成三角形
diagonal
bool diagonal(int i, int j, int n, const unsigned char* verts, const unsigned short* indices)
i和j分别为多边形的顶点(索引),此函数判断顶点i 顶点j的连线能否作为多边形的对角线
用图表示如下:

diagonal调用了一些工具函数,以下做一些简要说明
这四个函数大同小异
利用向量的叉积(即两个向量的夹角sin值),判断两个向量的方向关系
以leftOn为例向量V1 =b-a V2=c-a
V1 V2的叉积:
=0时 表示夹角为零(用于共线判断)
>0时 表示V1转到V2是顺时针,如下图:
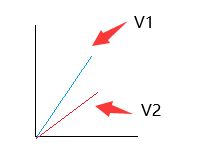
<0时 表示V1转到V2是逆时针, 此时V1 V2与上图相反
leftOn代码片段截取如下:

返回0:表示 a b c 三点共线
返回<0 表示 c 在向量ab的左边
返回>0 表示 c 在向量ab的右边
用右手,绕序abc,
大拇指朝上: c在ab右
大拇指朝下: c在ab左
工具函数inCone
此函数利用工具函数leftOn left保证一系列4个点是凸的
代码片段如下:

工具函数diagonalie
此函数排除与多边线相交的对角线,如下图

工具函数intersect
此函数判断两个线段是否相交
bool intersectProp(const unsigned char* a, const unsigned char* b, const unsigned char* c, const unsigned char* d)
这个函数利用left工具函数判断
1 点a和点b在线段cd的两边
2 点c和点d在线段ab的两边
如果满足1,2这两个条件,则说明线相交
bool between(const unsigned char* a, const unsigned char* b, const unsigned char* c)
利用area2判断是否共线,即叉积为0
在共线的情况下,判断端点是否交叠,交叠才能算相交
如果下图所示,要排除红蓝这种共线的方式,因为没有交叠
致此,triangulate函数中找合法对角线相关的函数大部分介绍完毕
切割三角形
根据合法的对象线,从多边形中切割出三角形
每次循环找出符合条件的对角线(程序中是长度最小)
根据对角线,把对应的顶点分离出去,形成一个三角形, 剩余的点形成新的多边形
多边形改变了,对受影响的点重新调用diagonal,计算对角线的合法性
如下图所示,沿着绿色虚线,切出三角形,

反复循环之后,多边形变成三角形,如下

致此,完成多边形三角化
3.4.2 合并三角形为凸多边形
好像不合并也行,三角形一定是凸的,合并后数据更少,执行效率更优
getPolyMergeValue
判断两个多边形是否有共同的边,
并且保证合并后是凸的,
返回值是公共边的长度
利用uleft来判断合并后是否是凸的,公共边的两个端点处都要判断,如下图:

代码片段如下:

mergePolys
合并多点边形,这个函数比较简单,复制数据,保证点的绕序,代码与相应的注释说明如下:

3.4.3 buildMeshAdjacency
生成多边形邻接信息
1 首先将所有的边,按顶点索引为key建立类哈希表
2 对具有相同顶点的边进行判断,是否为公共边
3 边连接
4 port连接
简单说一下有port连接,其实和普通的边连接是一样的
如下图, 根据扁平化规则, 黑色线处(水平的黑色和斜的黑色)的span和蓝色线处的span会被划分至不同layer

可回看addSpan 假设黑色斜的那一部分,在蓝色处形成投影,
投影边缘的那些点(假设是蓝色面的边线),
如果蓝色面周围有其它span邻居(假设是图中的红色,并且红色与黑色layer是同一个layer)
蓝色面的边缘span会变成port,并形成port连接
即port和 普通边连接可以认为不共存
部分代码片段如下:

如果是边连接,存放对应多边形的数组下标
如果是port,则要额外打个0x8000的标记,存port的方向(0,1,2,3)
这些数据会dtCreateNavMeshData里做转换
Port(0,1,2,3,4)会转成 4,2,0,6

3.4.4 dtNavMesh::addTile
将数据添加进tile,这一步要处理tile之间的连接
即不同的tile,要处理连缘处的多边形的连通情况,便于tile之间导航寻路
如果只是想了解Sample_SoloMesh的业务逻辑,可以跳过本段
connectIntLinks
这个函数负责生成tile之内多边形邻居信息生成(主要是相邻多边形的公共边)
findConnectingPolys
1 此函数负责查找tile之间的多边形连接情况
这种情况,记录的不是公共边,而是多边形相互靠近的两条边,它们的交叠部分记录下来
2 此函数也负责tile之间,不同层之间的连通情况,即因为port产生的连接
代码片段如下:

Port可以认为是高一层的layer在低上层的layer上投影的边缘的那些点
记录相邻边交叠部分的代码

致此,导航需要多边形邻接信息生成完毕,
之后就是利用这些信息进行寻路
4 寻路
4.1 dtNavMeshQuery::findPath 网格寻路
此函数没有太多难懂的地方
按网格邻接查找网格路径,类A*算法,按多边形中心点的距离估算cost
m_openList:是一个堆(极小堆),每个弹出一个cost最优的节点进行循环迭代
4.2 dtNavMeshQuery::findStraightPath 寻找拐点
得到一系列相邻的多边形路径, 如何穿过这些多边形, 需要此函数处理,即需要知道要在哪些地方拐弯
4.2.1 寻路初始
如下图所示,
从红点出发,要走到蓝点
用红色标出每个多边形的邻接边:

4.2.2 射线包络
对第一条邻边,从起始的红点,与邻接边的端点,发出一条射线(图中的紫线)
对第二条邻边也做同样的两条射线(图中的黄线)
两条紫射线为一组,两条黄射线为一组,取它们的交集,
以下图为例,交集显示是两条黄射线包络的那部分,

如下图,处理到第三条邻边时的最小包络射线

4.2.3 拐点出现的情况
对之后的每条邻边重复上面的循环,直到出现没有交集的情况
检测到拐点(粉红的那个点),
如下图,此例在红色邻边的两个端点,此时与紫色的包络线已经没有交集了

4.2.4 寻路结束
然后以粉色点为新的起点,重复以上过程,就可以找到一条在多边形内部的路径,
即最终的路径会是从红点走到粉点,再从粉点走到蓝色

4.2.5 结束语
致此,完成了导航网格生成与寻路功能说明
====================== 分割线 ============================
4.3 一些工具函数简介
寻路过程,使用了一些工具函数,以下做一个简要说明
dtDistancePtPolyEdgesSqr / dtPointInPolygon
利用射线与多边形的交点是奇偶判断是否在多边形内,
看代码射线应该是平行x轴往x轴正方向
代码片段如下:

dtDistancePtSegSqr2D
求点到线段的距离平方

dtTriArea2D
recast里有很多函数功能相似,此函数参考 leftOn
利用差乘判断线段与点的位置关系
getPortalPoints
获多边形邻边的两个端点(如果是tile间的连接或者port,取出交叠的首尾)
dtClosestHeightPointTriangle
利用射线(特殊射线,垂与xz平面的)与三角形的交点计算方法,求出射线与三角形的交点
三角形(p1 p2 p3)内部的顶点可以看到是
向量v1 = p3 - p1;
向量v2 = p2 - p1;
内部点 px = p1 + u*v1 + v*v2;
等同于: px = p1*(1-u-v) + p3*u + p2*v;
另外 px = O + d*t O:射线起点 d:射线方向 t:射线"长度"
O + d*t = p1*(1-u-v) + p3*u + p2*v; 这样可以得到一个三元一次方程组 未知数为(t u v)
根据克莱默法则解这个方组即可t u v 代入px = O + d*t即可得到对应的px坐标
同时,这个函数dtClosestHeightPointTriangle的射线是特殊的,垂直于xz平面



