欧拉函数

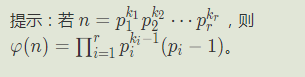
直接上代码：

#include <iostream>
using namespace std;
int euler(int n) {
    int res = n;
    for (int i = 2; i <= n; i++) {
        if (n % i == 0) {
            res = (1ll*res*(i-1))/i;
            while (n % i == 0) {
                n /= i;
            }
        }
    }
    return res;
}
int main() {
    int n;
    cin >> n;
    cout << euler(n) << endl;
    return 0;
}

 

或：

int euler(int n)//返回euler(n)
{
     int i;
     int res = n,a = n;
     for(i = 2;i*i <= a; ++i)
     {
         if(a%i == 0)
         {
             res -= res/i; //p(n) = (p - p/p1)(1 - 1/p2)......
             while(a%i == 0) a/=i;
         }
     }
     if(a > 1) res -= res/a;//存在大于sqrt(a)的质因子
     return res;
}

 

欧拉函数打表：

void SE()//select euler//类似于素数筛选法
{
    int i,j;
    euler[1] = 1;
    for(i = 2;i < Max; ++i)  euler[i]=i;
    for(i = 2;i < Max; ++i)
    {
         if(euler[i] == i)//这里出现的肯定是素数
         {
           for(j = i; j < Max; j += i)//然后更新含有它的数
           {
              euler[j] = euler[j]/i*(i - 1); // n*(1 - 1/p1)....*(1 - 1/pk).先除后乘
           }
        }
    }
     //for (int i = 1; i <= 20; ++i) printf("%d ",euler[i]);
}