深度学习编译器前端技术概述
AI 编译器在前端经常会做一些静态分析,方便在前端做一些优化:自动微分等。

中间表示(Intermediate Representation, IR)
IR 是编译器用于表示源代码的数据结构或代码,是程序编译过程中介于源语言和目标语言之间的程序表示。几乎所有的编译器都需要某种形式的中间表示,来对被分析、转换和优化的代码进行建模。
在编译过程中,中间表示必须具备足够的表达力,在不丢失信息的情况下准确表达源代码,并且充分考虑从源代码到目标代码编译的完备性、编译优化的易用性和性能。

上图中,在目标机器执行计算前,我们拿到了 IR 做了一些通用的优化,再送到后端去执行计算。
IR 的种类
| 组织结构 | 特点 | 举例 |
|---|---|---|
| Linear IR | 基于线性代码 | 堆栈机代码、三地址代码 |
| Graphical IR | 基于图 | 抽象语法树、有向无环图、控制流图 |
| Hybrid IR | 基于图与线性代码混合 | LLVM IR |
-
线性 IR
线性 IR 类似汇编代码,将被编译代码表示为操作的有序序列,对操作序列规定了一种清晰且实用的顺序。由于大多数处理器采用线性的汇编语言,线性中间表示广泛应用于编译器设计。
简单来说,线性 IR 相当于是用类似汇编和伪代码的语言来描述我们的程序。
常用线性 IR 有堆栈机代码(Stack-Machine Code)和三地址代码(Three Address Code) 。堆栈机代码是一种单地址代码,提供了简单紧凑的表示。堆栈机代码的指令通常只有一个操作码,其操作数存在一个栈中。大多数操作指令从栈获得操作数,并将其结果推入栈中。三地址代码,简称为3AC,模拟了现代RISC机器的指令格式。它通过一组四元组实现,每个四元组包括一个运算符和三个地址(两个操作数、一个目标)。
下图是表达式
a - b * 5的两种线性 IR:
-
图 IR
图 IR 将编译过程的信息保存在图中,算法通过图中的对象如节点、边、列表、树等来表述。虽然所有的图中间表示都包含节点和边,但在抽象层次、图结构等方面各有不同。常见的图中间表示包括抽象语法树(Abstract Syntax Tree,AST)、有向无环图(Directed Acyclic Graph,DAG)、控制流图(Control-Flow Graph,CFG)等。
下面是表达式
a * 5 + a * 5 * b的 AST 和 DAG: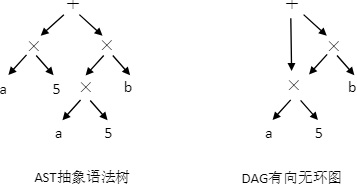
可以看出来 DAG 相比 AST 在这里复用了
a * 5,如果编译器可以证明 a 的值没有改变的话, DAG 可以重用 a * 5 这个子树,降低求值过程的开销。 -
混合 IR
混合中间表示是线性中间表示和图中间表示的结合,这里以 LLVM IR 为例进行说明。
LLVM(Low Level Virtual Machine) 是 2000 年提出的开源编译器框架项目,旨在为不同的前端后端提供统一的中间表示。LLVM IR 使用线性 IR 表示基本块,使用图 IR 表示这些块之间的控制流。基本块中,每条指令以静态单赋值(Static Single Assignment, SSA) 形式呈现,这些指令构成一个指令线性列表。SSA形式要求每个变量只赋值一次,并且每个变量在使用之前定义。控制流图中,每个节点为一个基本块,基本块之间通过边实现控制转移。

机器学习框架的 IR
传统 IR 如LLVM IR,能够很好地满足通用编译器的基本功能需求,包括类型系统、控制流和数据流分析等。然而,它们偏向机器语言,难以满足机器学习框架编译器的中间表示的需求。
在设计机器学习框架的中间表示时,需要充分考虑以下因素:
-
张量表达
机器学习框架主要处理张量数据,因此正确处理张量数据类型是机器学习框架中间表示的基本要求;
-
自动微分
动微分是指对网络模型的自动求导,通过梯度指导对网络权重的优化。主流机器学习框架都提供了自动微分的功能,在设计中间表示时需要考虑自动微分实现的简洁性、性能以及高阶微分的扩展能力;
-
计算图模式
主流机器学习框架都支持静态图和动态图,两种计算图各有各的优缺点。
机器学习框架的 IR 设计应该同时支持静态图和动态图,可以针对待解决的任务需求,选择合适的模式构建算法模型;
-
编译优化
机器学习框架的编译优化主要包括硬件无关的优化、硬件相关的优化、部署推理相关的优化等,这些优化都依赖于 IR 的实现。比如 tvm 的 TensorIR 就会做一些通用的优化;
-
JIT (Just in Time) 能力
机器学习框架进行编译执行加速时,经常用到 JIT 即时编译。JIT 编译优化将会对 IR 中的数据流图的可优化部分实施优化,包括循环展开、融合、内联等。IR 设计是否合理,将会影响机器学习框架的 JIT 编译性能和程序的运行能力。
主流机器学习框架的 IR
-
PyTorch
PyTorch 是一个基于动态计算图机制的机器学习框架,以 Python 优先,具有很强的易用性和灵活性,方便用户编写和调试网络代码。为了保存和加载网络模型,PyTorch 提供了 TorchScript 方法,用于创建可序列化和可优化模型。TorchScript IR 作为 PyTorch 模型的中间表示,通过 JIT 即时编译的形式,将 Python 代码转换成目标模型文件。任何 TorchScript 程序都可以在 Python 进程中保存,并加载到没有 Python 依赖的进程中。
PyTorch 采用命令式编程方式,其 TorchScript IR 以基于 SSA 的线性 IR 为基本组成形式,并通过 JIT 即时编译的 Tracing 和 Scripting 两种方法将 Python 代码转换成 TorchScript IR。如下 Python代码使用了 Scripting 方法并打印其对应的中间表示图:
importtorch @torch.jit.script def test_func(input): rv = 10.0 for i in range(5): rv = rv + input rv = rv/2 return rv print(test_func.graph)IR 的结构为:
graph(%input.1 : Tensor): %9 : int = prim::Constant[value=1]() %5 : bool = prim::Constant[value=1]() # test.py:6:1 %rv.1 : float = prim::Constant[value=10.]() # test.py:5:6 %2 : int = prim::Constant[value=5]() # test.py:6:16 %14 : int = prim::Constant[value=2]() # test.py:8:10 %rv : float = prim::Loop(%2, %5, %rv.1) # test.py:6:1 block0(%i : int, %rv.9 : float): %rv.3 : Tensor = aten::add(%input.1, %rv.9, %9) # <string>:5:9 %12 : float = aten::FloatImplicit(%rv.3) # test.py:7:2 %rv.6 : float = aten::div(%12, %14) # test.py:8:7 -> (%5, %rv.6) return (%rv)TorchScript 是 PyTorch 的 JIT 实现,支持使用 Python 训练模型,然后通过 JIT 转换为语言无关的模块,从而提升模型部署能力,提高编译性能。同时,TorchScript IR 显著改善了 Pytorch 的模型可视化效果。
-
JAX
Jax 同时支持静态图和动态图,其中间表示采用 Jaxpr(JAX Program Representation) IR。Jaxpr IR是一种强类型、纯函数的中间表示,其输入、输出都带有类型信息,函数输出只依赖输入,不依赖全局变量。
Jaxpr IR 的表达采用 ANF(A-norm Form) 函数式表达形式,ANF 文法如下所示:
<aexp> ::= NUMBER | STRING | VAR | BOOLEAN | PRIMOP | (lambda (VAR ...) <exp>) <cexp> ::= (<aexp> <aexp> ...) | (if <aexp> <exp> <exp>) <exp> ::= (let ([VAR <cexp>]) <exp>) | <cexp> | <aexp>ANF 形式将表达式划分为两类:原子表达式(aexp)和复合表达式(cexp)。原子表达式用于表示常数、变量、原语、匿名函数,复合表达式由多个原子表达式组成,可看作一个匿名函数或原语函数调用,组合的第一个输入是调用的函数,其余输入是调用的参数。如下代码打印了一个函数对应的 JaxPr:
from jax import make_jaxpr import jax.numpy as jnp def test_func(x, y): ret = x + jnp.sin(y) * 3 return jnp.sum(ret) print(make_jaxpr(test_func)(jnp.zeros(8), jnp.ones(8)))其对应的 JaxPr 为:
{ lambda ; a:f32[8] b:f32[8]. let c:f32[8] = sin b d:f32[8] = mul c 3.0 e:f32[8] = add a d f:f32[] = reduce_sum[axes=(0,)] e in (f,) }Jax 结合了 Autograd 和 JIT,基于Jaxpr IR,支持循环、分支、递归、闭包函数求导以及三阶求导,并且支持自动微分的反向传播和前向传播。
-
TensorFlow
TensorFlow 同时支持静态图和动态图,是一个基于数据流编程的机器学习框架,使用数据流图作为数据结构进行各种数值计算。TensorFlow 的静态图机制更为人所熟知。在静态图机制中,运行 TensorFlow 的程序会经历一系列的抽象以及分析,程序会逐步从高层的 IR 向底层的 IR 进行转换,我们把这种变换成为 lowering。

-
MLIR
MLIR 不是一种具体的 IR 定义,而是为 IR 提供一个统一的抽象表达和概念。 开发者可以使用 MLIR 开发的一系列基础设施,来定义符合自己需求的 IR , 因此我们可以把 MLIR 理解为“编译器的编译器”。
MLIR 通过 Dialect 的概念来支持这种可拓展性, Dialect 在特定的命名空间下为抽象提供了分组机制,分别为每种中间表示定义对应的产生式并绑定相应的 Operation, 从而生成一个 MLIR 类型的中间表示。Operation 是 MLIR 中抽象和计算的核心单元,其具有特定的语意,可以用于表示 LLVM 中所有核心的IR结构, 例如指令, 函数以及模块等。 如下就是一个 MLIR 定义下的Operation:
%tensor = "toy.transpose"(%tensor) {inplace = true} : (tensor<2x3xf64>) -> tensor<3x2xf64> loc("example/file/path":12:1)- % tensor: Operation 定义的结果的名字, % 是为了避免冲突统一加入的。一个 Operation 可以定义 0 或者多个结果,它们是 SSA 值。
- “toy.transpose”: Operation的 名字。它是一个唯一的字符串,其中 Dialect 为 Toy。因此它可以理解为 Toy Dialect 中的 transpose Operation。
- (%tensor):输入操作数(或参数)的列表,它们是由其它操作定义或引用块参数的 SSA 值。
- {inplace = true}:零个或多个属性的字典,这些属性是始终为常量的特殊操作数。在这里,我们定义了一个名为“inplace”的布尔属性,它的常量值为 true。
- (tensor<2x3xf64>)->tensor<3x2xf64>:函数形式表示的操作类型,前者是输入,后者是输出。尖括号内代表输入与输出的数据类型以及形状, 例如 <2x3xf64> 代表一个形状为 2X3, 数据类型为float64的张量。
- loc(“example/file/path”:12:1):此操作的源代码中的位置。
由于各层 IR 都遵循如上的样式进行定义,所以各个层级的 IR 之间可以更加方便的进行转换, 提高了 IR 转换的效率。各个不同层级的 IR 还可以协同进行优化。 此外,由于 IR 之间不再相互独立, 各层级的优化不必做到极致,而是可以将优化放到最适合的层级。 其他的中间表示只需要先转换为该层级的 IR,就可以进行相关的优化,提高了优化的效率与开发效率。
自动微分
自动微分(Automatic Differentiation, AD)是一种介于符号微分和数值微分之间的针对计算图进行符号解析的求导方法,用于计算函数梯度值。主流的深度学习框架都支持自动微分(因为手动计算导数太麻烦了)。自动微分在深度学习中处于非常重要的地位,是整个训练算法的核心组件之一。自动微分通常在编译器前端优化中实现,通过对中间表示的符号解析来生成带有梯度函数的中间表示。
自动微分(Automatic Differentiation,AD)是一种对计算机程序进行高效且准确求导的技术。随着近些年深度学习在越来越多的机器学习任务上取得领先成果,自动微分被广泛的应用于机器学习领域。许多机器学习模型使用的优化算法都需要获取模型的导数,因此自动微分技术成为了一些热门的机器学习框架的核心特性。
常见的计算机程序求导的方法可以归纳为以下四种 :手工微分(Manual Differentiation)、数值微分(Numerical Differentiation)、符号微分(Symbolic Differentiation)和自动微分(Automatic Differentiation)。
(1)手工微分:需手工求解函数导数的表达式,并在程序运行时根据输入的数值直接计算结果。手工微分需根据函数的变化重新推导表达式,工作量大且容易出错。
2)数值微分:数值微分通过差分近似方法完成,其本质是根据导数的定义推导而来。
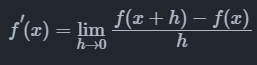
当 h 充分小时,可以用差分 $\frac{f(x+h)-f(x)}{h}$ 来近似导数结果。而近似的一部分误差,称为截断误差(Truncation error)。理论上,数值微分中的截断误差与步长 h 有关,h 越小则截断误差越小,近似程度越高。但实际情况下数值微分的精确度并不会随着 h 的减小而一直减小。这是因为计算机系统对于浮点数运算的精度有限导致另外一种误差的存在,这种误差称为舍入误差(Round-off Error)。舍入误差会随着 h 变小而逐渐增大。当 h 较大时,截断误差占主导。而当 h较小时,舍入误差占主导。 在截断误差和舍入误差的共同作用下,数值微分的精度将会在某一个h 值处达到最小值,并不会无限的减小。因此,虽然数值微分容易实现,但是存在精度误差问题。
(3)符号微分:利用计算机程序自动地通过如下的数学规则对函数表达式进行递归变换来完成求导。
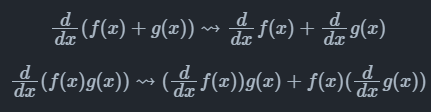
符号微分虽然消除了手工微分硬编码的缺陷。但因为对表达式进行严格的递归变换和展开,不复用产生的变换结果,很容易产生表达式膨胀问题。用符号微分计算递归表达式 $l_{n+1}=4l_n(1-l_n)$,$l_1=x$ 的导数表达式,其结果随着迭代次数增加快速膨胀。

并且符号微分需要表达式被定义成闭合式的(closed-form),不能带有或者严格限制控制流的语句表达,使用符号微分会很大程度上地限制了机器学习框架网络的设计与表达。
(4)自动微分:自动微分的思想是将计算机程序中的运算操作分解为一个有限的基本操作集合,且集合中基本操作的求导规则均为已知,在完成每一个基本操作的求导后,使用链式法则将结果组合得到整体程序的求导结果。自动微分是一种介于数值微分和符号微分之间的求导方法,结合了数值微分和符号微分的思想。相比于数值微分,自动微分可以精确地计算函数的导数;相比符号微分,自动微分将程序分解为基本表达式的组合,仅对基本表达式应用符号微分规则,并复用每一个基本表达式的求导结果,从而避免了符号微分中的表达式膨胀问题。而且自动微分可以处理分支、循环和递归等控制流语句。目前的深度学习框架基本都采用自动微分机制进行求导运算,下面我们将重点介绍自动微分机制以及自动微分的实现。
前向与反向自动微分
自动微分根据链式法则的不同组合顺序,可以分为前向模式(Forward Mode)和反向模式(Reverse Mode)。对于一个复合函数$y=a(b(c(x)))$,其梯度值$\frac{dy}{dx}$的计算公式为:
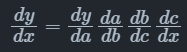
前向模式的自动微分是从输入方向开始计算梯度值的,其计算公式为:
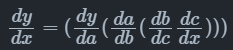
反向模式的自动微分是从输出方向开始计算梯度值的,其计算公式为:
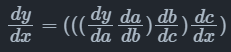
我们以下面的函数为例介绍两种模式的计算方式,我们希望计算函数在$(x_1, x_2)=(2,5)$处的导数$\frac{\partial y}{\partial x_1}$:

该函数对应的计算图:
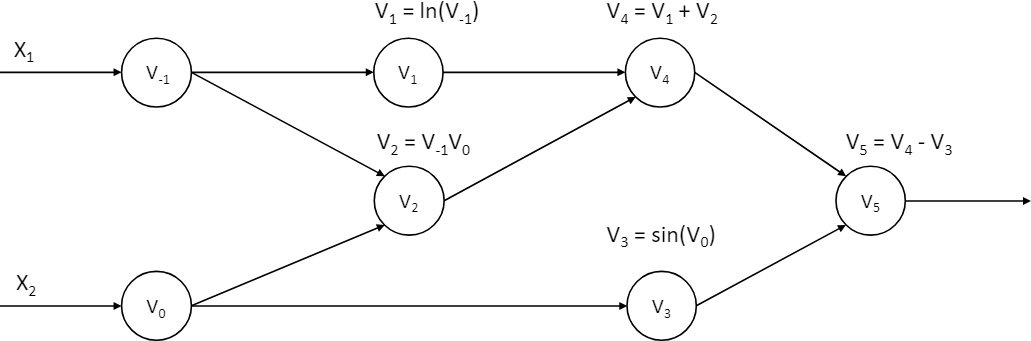
(1)前向模式

(2)反向模式

自动微分的实现
PyTorch 和 MegEngine 主要采用操作符重载法(Operator Overloading, OO),依赖于现代编程语言的多态特性,使用操作符重载对编程语言中的基本操作语义进行重定义,封装其微分规则。每个基本操作类型及其输入关系,在程序运行时会被记录在一个所谓的"tape"的数据结构里面,最后,这些"tape"会形成一个跟踪轨迹(trace),我们就可以使用链式法则沿着轨迹正向或者反向地将基本操作组成起来进行微分。以自动微分库 AutoDiff 为例,对编程语言的基本运算操作符进行了重载:
namespace AutoDiff
{
public abstract class Term
{
// 重载操作符 `+`,`*` 和 `/`,调用这些操作符时,会通过其中的
// TermBuilder 将操作的类型、输入输出信息等记录至 tape 中
public static Term operator+(Term left, Term right)
{
return TermBuilder.Sum(left, right);
}
public static Term operator*(Term left, Term right)
{
return TermBuilder.Product(left, right);
}
public static Term operator/(Term numerator, Term denominator)
{
return TermBuilder.Product(numerator, TermBuilder.Power(denominator, -1));
}
}
// Tape 数据结构中的基本元素,主要包含:
// 1) 操作的运算结果
// 2) 操作的运算结果对应的导数结果
// 3) 操作的输入
// 除此外还通过函数 Eval 和 Diff 定义了该运算操作的计算规则和微分规则
internal abstract class TapeElement
{
public double Value;
public double Adjoint;
public InputEdges Inputs;
public abstract void Eval();
public abstract void Diff();
}
}
OO 对程序的运行跟踪经过了函数调用和控制流,因此实现起来也是简单直接。而缺点是需要在程序运行时进行跟踪,特别在反向模式上还需要沿着轨迹反向地执行微分,所以会造成性能上的损耗,尤其对于本来运行就很快的基本操作。并且因为其运行时跟踪程序的特性,该方法不允许在运行前做编译时刻的图优化,控制流也需要根据运行时的信息来展开。
类型系统与静态分析
为了有效减少程序在运行时可能出现的错误,编译器的前端引入了类型系统(Type System)和静态分析(Static Analysis)系统。类型系统可以防止程序在运行时发生类型错误,而静态分析能够为编译优化提供线索和信息,有效减少代码中存在的结构性错误、安全漏洞等问题。
类型系统提供的主要功能有:
1)正确性。编译器的类型系统引入了类型检查技术,用于检测和避免运行时错误,确保程序运行时的安全性。通过类型推导与检查,编译器能够捕获大多数类型相关的异常报错,避免执行病态程序导致运行时错误,保证内存安全,避免类型间的无效计算和语义上的逻辑错误。
以 MegEngine 为例,发 kernel 之前会做一些 shape、dtype 的检查:https://github.com/MegEngine/MegEngine/blob/master/imperative/src/impl/ops/convolution.cpp#L28
如果有问题的话,在发 kernel 之前就报错。
2)优化。静态类型检查可以提供有用的信息给编译器,从而使得编译器可以应用更有效的指令,节省运行时的时间。
3)抽象。在安全的前提下,一个强大的类型系统的标准是抽象能力。通过合理设计抽象,开发者可以更关注更高层次的设计。
4)可读性。阅读代码时,明确的类型声明有助于理解程序代码。
在设计好类型系统后,编译器需要使用静态分析系统来对中间表示进行静态检查与分析。语法解析模块(parser)将程序代码解析为抽象语法树(AST)并生成中间表示。此时的中间表示缺少类型系统中定义的抽象信息,因此引入静态分析模块,对中间表示进行处理分析,并且生成一个静态强类型的中间表示,用于后续的编译优化、自动并行以及自动微分等。在编译器前端的编译过程中,静态分析可能会被执行多次,有些框架还会通过静态分析的结果判断是否终止编译优化。
静态分析模块基于抽象释义对中间表示进行类型推导、常量传播、泛型特化等操作,这些专业术语的含义分别为:
抽象释义:通过抽象解释器将语言的实际语义近似为抽象语义,只获取后续优化需要的属性,进行不确定性的解释执行。抽象值一般包括变量的类型和维度。
类型推导:在抽象释义的基础上,编译器推断出程序中变量或表达式的抽象类型,方便后续利用类型信息进行编译优化。
泛型特化:泛型特化的前提是编译器在编译期间可以进行类型推导,提供类型的上下文。在编译期间,编译器通过类型推导确定调用函数时的类型,然后,编译器会通过泛型特化,进行类型取代,为每个类型生成一个对应的函数方法。
挖坑: MegEngine 的静态分析流程
前端编译优化
编译优化意在解决代码的低效性,无论是在传统编译器还是在机器学习框架中都起着很重要的作用。前端的编译优化与硬件无关,前端编译优化大多是一些较通用的优化,比如常量替换、死代码擦除等。
大多数编译优化器会由一系列的”趟”(Pass)来组成。每个”趟”以 IR 为输入,又以新生成的 IR 为输出。一个”趟”还可以由几个小的”趟”所组成。一个”趟”可以运行一次,也可以运行多次。
在编译优化中,优化操作的选择以及顺序对于编译的整体具有非常关键的作用。优化操作的选择决定了优化器能够感知 IR 中的哪些低效性,也决定了编译器将要如何去重写 IR 以消除这种低效性。优化操作的顺序决定了各趟操作的执行顺序。编译器可以根据具体需要运行不同的编译优化操作。也可以根据编译优化级别来调整优化的次数,种类以及顺序。
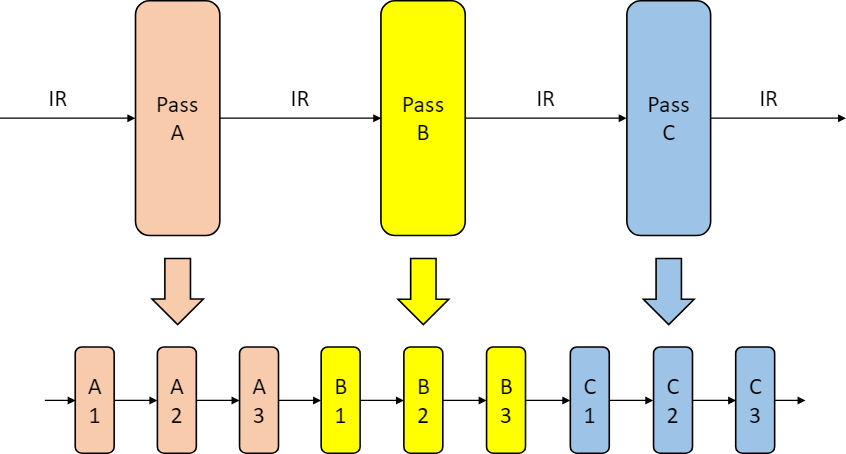
上图中 IR 经过 pass 后被编译器处理成新的 IR 结构(也就是编译器认为执行起来效率更高的等价结构)。
常见编译优化方法
-
死代码(无用及不可达代码)消除
无用代码是指输出结果没有被任何其他代码所使用的代码。不可达代码是指没有有效的控制流路径包含该代码。删除无用或不可达的代码可以使得 IR 更小,提高程序的编译与执行速度。无用与不可达代码一方面有可能来自于程序编写者的编写失误,也有可能是其他编译优化所产生的结果。
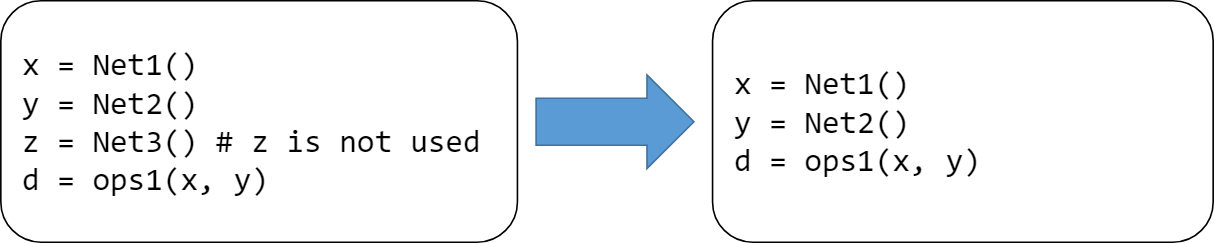
-
常量传播 / 折叠
常量传播:如果某些量为已知值的常量,那么可以在编译时刻将使用这些量的地方进行替换。
常量折叠:多个量进行计算时,如果能够在编译时刻直接计算出其结果,那么变量将由常量替换。

-
公共表达式消除
如果一个表达式 E 已经计算过了,并且从先前的计算到现在E中所有变量的值都没有发生变化,那么 E 就成为了公共子表达式。对于这种表达式,没有必要花时间再对它进行计算,只需要直接用前面计算过的表达式结果代替 E 就可以了。
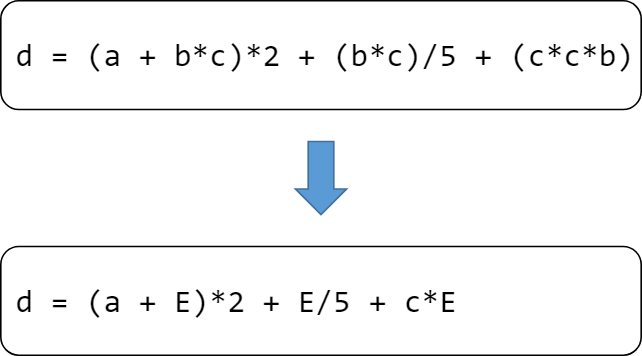





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律
2020-08-06 LeetCode166. 分数到小数
2020-08-06 LeetCode165. 比较版本号