LeetCode84. 柱状图中最大的矩形

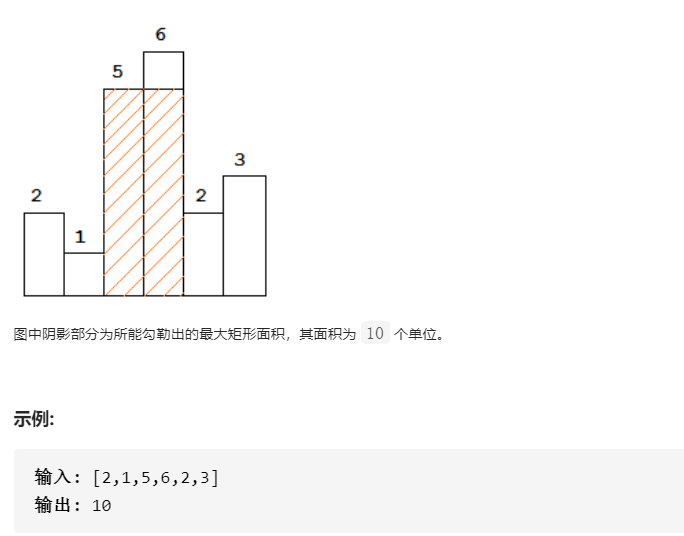
要求能勾勒出来的矩形的最大高度，很自然的想法就是枚举所有矩形的宽度和高度，再通过高度和宽度的乘积求出所有矩形的面积，这样就可以知道最大矩形的面积了。

暴力做法是，枚举所有矩形的宽度（也就是枚举左边界和右边界），再求出左边界和右边界内柱子的最小高度（瓶颈高度），然后得到矩形的面积。
代码如下：

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int size = heights.size();
        long long res = 0;
        for(auto height : heights) {
            res = res > height ? res : height;
        }
        for(int i = 0; i < size; ++i) {
            for(int j = i + 1; j < size; ++i) {
                long long width = j - i + 1, minHeight = INT_MAX;
                for(int k = i; k <= j; ++k) {
                    minHeight = minHeight < heights[k] ? minHeight : heights[k];
                }
                res = max(res, width * minHeight);
            }
        }
        return res;
    }
};

枚举左右边界有两层循环，另外还要再求左右边界内的最小高度。最坏情况下时间复杂度会达到O(n^3)，超时。

我们可以换个思路，暴力做法是先固定宽度再求高度，我们可以固定高度再求宽度。

因为对于每一个矩形，它的高度肯定是某个柱子的高度（当前矩形所有柱子里的瓶颈高度），所以对于所有柱子，将它作为瓶颈，分别往左右寻找可以达到的最远距离，这个最远距离就是矩形的宽度，再乘上这个柱子的高度，就是当前矩形的面积。

可以枚举一遍所有柱子，就知道当前矩形的瓶颈高度了，那么往左右可以到达的最远距离怎么求呢？
我们可以观察一下，什么情况下最远距离可以往左右延伸。

在固定了高度的情况下，如果当前柱子的高度就是矩形的最低高度的情况下，那么宽度（最远距离）内所有其他柱子的高度都必须大于等于当前柱子的高度，如果小于当前柱子的高度，则我们找到了边界。

比如对于样例[2, 1, 5, 6, 2, 3]，对于5，往左第一个数1就比它小了，则我们找到了左边界，就是1的下一个数（5自己），往右，6比5大，继续往油找，2比5小，则找到了右边界，2的上一个数（6），所以宽度就是3(6的下标） - 2(5的下标) + 1 = 2，再乘上当前柱子的高度5，就得到当前矩形的面积10.

所以问题就转化为，对于每一个柱子，分别求出左边和右边的离当前柱子最近的比当前柱子高度小的柱子的高度。

这实际上就是单调栈解决的问题。单调栈的模型就是用来求一个数的离他最近的比它小的数。

只不过这题，我们不止要求左边的第一个比它小的数，还要求右边的第一个比它小的数，所以，我们可以开两个数组left和right，还有两个栈stack1和stack2。

left[i]表示在第i个数往左边第一个比它小的数的下标，right[i]表示第i个数往右边第一个比它小的数的下标。
stack1就是从左往右用来求left数组的单调栈，stack2是从右往左用来求right数组的单调栈。

这样，我们可以用两个O(n)（单调栈的时间复杂度）求出每个柱子的left和right（左右第一个比它矮的柱子），然后得到的宽度和当前柱子的高度相乘就是矩形的面积。
整个算法的时间复杂度是O(n)。

代码如下：

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int size = heights.size();
        vector<int> left(size), right(size);
        stack<int> stack1, stack2;
        for(int i = 0; i < size; ++i) {
            while(!stack1.empty() && heights[stack1.top()] >= heights[i]) {
                stack1.pop();
            }
            if(stack1.empty()) {
                left[i] = -1;                  //如果栈为空，说明往左边所有柱子都比当前柱子高，则左边界直接取到-1
            } else {
                left[i] = stack1.top();
            }
            stack1.push(i);
        }
        for(int i = size - 1; i >= 0; --i) {
            while(!stack2.empty() && heights[stack2.top()] >= heights[i]) {
                stack2.pop();
            }
            if(stack2.empty()) {            //如果栈为空，说明往右边所有柱子都比当前柱子高，则左边界直接取到size
                right[i] = size;
            } else {
                right[i] = stack2.top();
            }
            stack2.push(i);
        }
        int res = 0;
        for(int i = 0; i < size; ++i) {                  //对于每个矩形的面积，更新res
            res = max(res, heights[i] * (right[i] - left[i] - 1));
        }
        return res;
    }
};

进一步优化一下空间，可以只用一个栈，不必开两个栈求left和right数组，只需要在第二个for循环之前将栈请客即可。

stk = stack<int>();

其他部分是一样的，代码如下：

class Solution {
public:
    int largestRectangleArea(vector<int>& heights) {
        int size = heights.size();
        vector<int> left(size), right(size);
        stack<int> stk;
        for(int i = 0; i < size; ++i) {
            while(!stk.empty() && heights[stk.top()] >= heights[i]) {
                stk.pop();
            }
            if(stk.empty()) {
                left[i] = -1;
            } else {
                left[i] = stk.top();
            }
            stk.push(i);
        }
        stk = stack<int>();
        for(int i = size - 1; i >= 0; --i) {
            while(!stk.empty() && heights[stk.top()] >= heights[i]) {
                stk.pop();
            }
            if(stk.empty()) {
                right[i] = size;
            } else {
                right[i] = stk.top();
            }
            stk.push(i);
        }
        int res = 0;
        for(int i = 0; i < size; ++i) {
            res = max(res, heights[i] * (right[i] - left[i] - 1));
        }
        return res;
    }
};