查找算法
顺序查找
- 当数据存储在诸如列表的集合中时,我们说这些数据具有线性或顺序关系。 每个数据元素都存储在相对于其他数据元素的位置。 由于这些索引值是有序的,我们可以按顺序访问它们。 这个过程产实现的搜索即为顺序查找。
- 顺序查找原理剖析:
- 从列表中的第一个元素开始,我们按照基本的顺序排序,简单地从一个元素移动到另一个元素,直到找到我们正在寻找的元素或遍历完整个列表。如果我们遍历完整个列表,则说明正在搜索的元素不存在。
- 代码实现:该函数需要一个列表和我们正在寻找的元素作为参数,并返回一个是否存在的布尔值。find 布尔变量初始化为 False,如果我们发现列表中的元素,则赋值为 True。
def search(alist,item):
find = False
pos = 0
while True:
if alist[pos] == item:
find = True
break
else:
pos += 1
if pos == len(alist):
break
return find
l = [1,2,3,4,5]
print(search(l,3)) # True
有序列表:之前我们列表中的元素是随机放置的,因此在元素之间没有相对顺序。如果元素以某种方式排序,顺序查找会发生什么?我们能够在搜索技术中取得更好的效率吗?
def search(alist,item):
cur = 0
find = False
while True:
if alist[cur] == item:
find = True
break
elif alist[cur] > item:
break
else:
cur += 1
if cur == len(alist):
break
return find
l = [1,2,3,4,5]
print(search(l,51)) # False
二分查找 (前提得是有序列表)
- 有序列表对于我们的实现搜索是很有用的。在顺序查找中,当我们与第一个元素进行比较时,如果第一个元素不是我们要查找的,则最多还有 n-1 个元素需要进行比较。 二分查找则是从中间元素开始,而不是按顺序查找列表。 如果该元素是我们正在寻找的元素,我们就完成了查找。 如果它不是,我们可以使用列表的有序性质来消除剩余元素的一半。如果我们正在查找的元素大于中间元素,就可以消除中间元素以及比中间元素小的一半元素。如果该元素在列表中,肯定在大的那半部分。然后我们可以用大的半部分重复该过程,继续从中间元素开始,将其与我们正在寻找的内容进行比较。
def find(alist, item):
left = 0 # 序列第一个元素下标
right = len(alist) - 1 # 序列中最后一个元素下标
find = False
while left <= right:
mid = (left + right) // 2 # 中间元素的下标,注意放入循环内部
if item == alist[mid]: # 找到了查找的值
find = True
break
else:
if item < alist[mid]: # 查找的值可能存在于中间元素左侧
right = mid - 1
# left和right表示中间元素左侧的子序列
else: # 查找的值是存在于中间元素右侧
left = mid + 1
return find
alist = [1,2,3,4,5,6,7,8,9]
print(find(alist,3)) # True
冒泡排序
- 1.将序列中两两元素比较,将其最大值逐一的移动到序列末尾的位置 (一步步的往后偏移)
- 2.将上述操作作用于前n-1个元素,n-2,...以此类推循环循环
step1
将序列中两两元素比较,将其最大值逐一的移动到序列末尾的位置
# step1:.将序列中两两元素比较,将其最大值逐一的移动到序列末尾的位置
def sort(alist):
for i in range(len(alist)-1):
if alist[i] > alist[i + 1]:
alist[i],alist[i+1] = alist[i+1],alist[i]
return alist
alist = [3,8,7,5,7,6,2,1]
print(sort(alist)) # [3, 7, 5, 7, 6, 2, 1, 8]
step2(冒泡排序最终实现)
将上述操作作用于前n-1个元素,n-2,...以此类推循环循环
# step2:将上述操作作用于前n-1个元素,n-2,...以此类推循环循环
def sort(alist):
for j in range(len(alist)-1):
for i in range(len(alist)-1-j):
if alist[i] > alist[i+1]:
alist[i],alist[i+1] = alist[i+1],alist[i]
return alist
alist = [3,8,7,5,7,6,2,1]
print(sort(alist)) # [1, 2, 3, 5, 6, 7, 7, 8]
选择排序
- 1.将乱序序列中的元素两两比较,将其最大值找出,直接和最后一个元素交换位置
- 2.循环第一步
step1
将乱序序列中的元素两两比较,将其最大值找出,直接和最后一个元素交换位置
# step1:将乱序序列中的元素两两比较,将其最大值找出,直接和最后一个元素交换位置
def sort(alist):
max_index = 0 # 永远保存最大值下标,一开始假设第0个元素为最大值
for i in range(1, len(alist)):
if alist[i] > alist[max_index]:
max_index = i
alist[max_index], alist[len(alist)-1] = alist[len(alist)-1], alist[max_index]
return alist
alist = [3,4,8,7,5,7,6,2,1]
print(sort(alist)) # [3, 4, 1, 7, 5, 7, 6, 2, 8]
step2(选择排序最终实现)
将上述操作作用于前n-1个元素,n-2,...以此类推循环循环
# step2:将上述操作作用于前n-1个元素,n-2,...以此类推循环循环
def sort(alist):
for j in range(len(alist)):
max_index = 0
for i in range(1,len(alist)-j):
if alist[i] > alist[max_index]:
max_index = i
alist[max_index],alist[len(alist)-1-j] = alist[len(alist)-1-j],alist[max_index]
return alist
alist = [3,4,8,7,5,7,6,2,1]
print(sort(alist)) # [1, 2, 3, 4, 5, 6, 7, 7, 8]
冒泡排序和选择排序的时间复杂度差不多
插入排序
- 将乱序的序列假设分为两部分
- 有序部分:默认情况下将序列第一个元素作为有序部分的第一个元素值
- 必须保证每刻都是有序
- 无序部分:n-1个元素作为无序部分的元素
- 需要将无序部分的每一个元素注意插入到有序部分中几个
- 有序部分:默认情况下将序列第一个元素作为有序部分的第一个元素值
- - [9, 8,5,11,10]
- - [8,9, 5,11,10]
- - [8,5,9, 11,10]
- - [5,8,9,11, 10]
- - [5,8,9,10,11 ]
启蒙
# i为有序部分的元素个数
i = 1
# alist[i]:无序部分中第一个元素
# alist[i-1]:有序部分的最后一个元素
if alist[i] < alist[i-1]:
alist[i],alist[i-1] = alist[i-1],alist[i]
i = 2
while i > 0:
if alist[i] < alist[i-1]:
alist[i],alist[i-1] = alist[i-1],alist[i]
i -= 1
else: # 如果无续的第一个元素大于有序最后元素,就不做操作
break
插入排序最终版
# 完整代码
def sort(alist):
for i in range(1,len(alist)):
while i > 0:
if alist[i] < alist[i-1]:
alist[i],alist[i-1] = alist[i-1],alist[i]
i -= 1
else: # 如果无续的第一个元素大于有序最后元素,就不做操作
break
return alist
alist = [9,8,5,11,10]
print(sort(alist) # [5, 8, 9, 11, 10]
希尔排序
也称缩小增量排序分组之后对组内进行排序 (乱序序列数据量比较大,乱序幅度比较大,希尔排序比插入排序时间效率更高)
- 增量gap:
- 分组的组数
- 每组数据间的间隔
- 插入排序其实就是增量为1的希尔排序
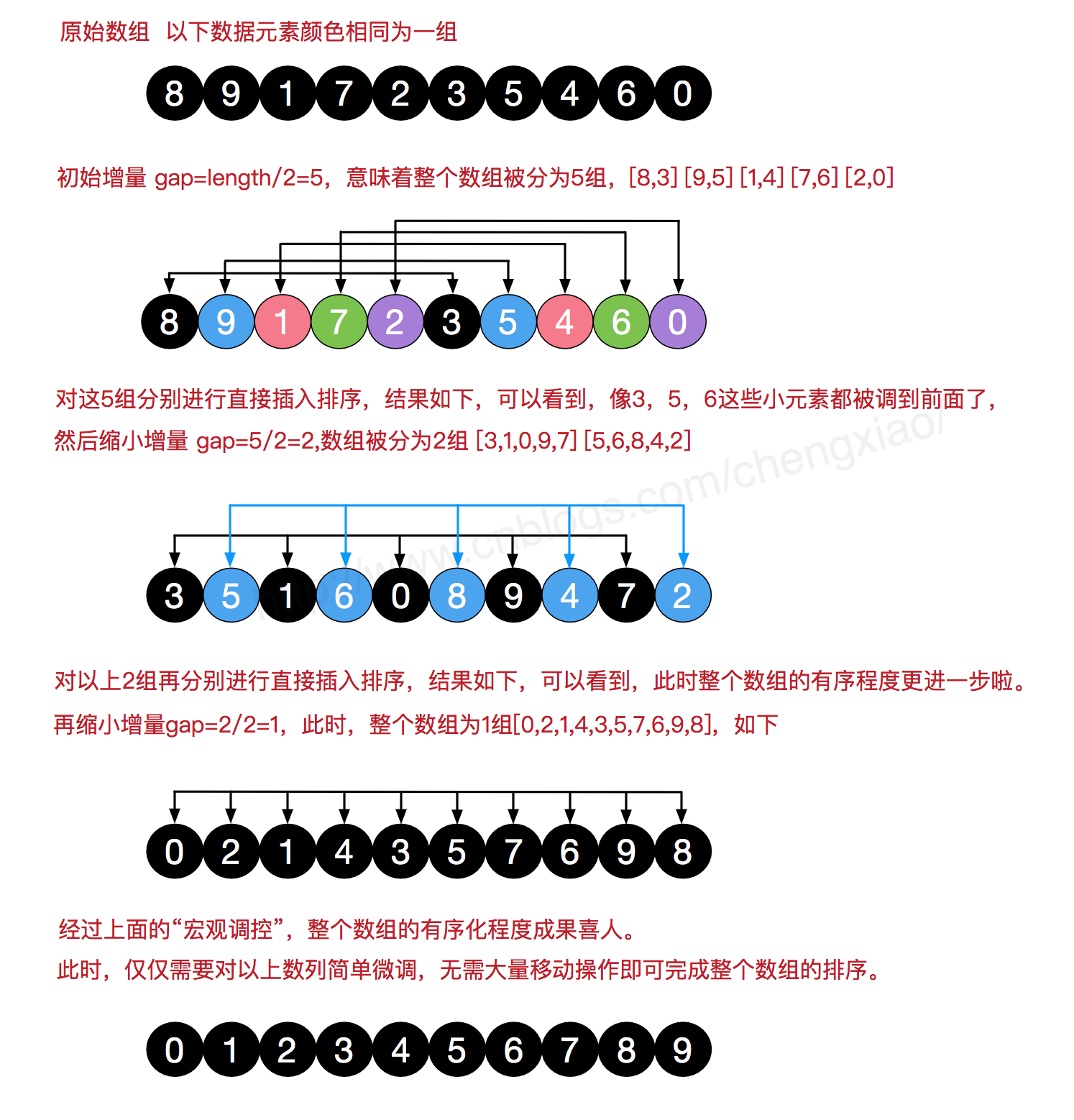
step1
# 1.加入增量gap,然后将插入排序代码的1改为gap
def sort(alist):
gap = len(alist) // 2
for i in range(gap,len(alist)):
while i > 0:
if alist[i] < alist[i-gap]:
alist[i],alist[i-gap] = alist[i-gap],alist[i]
i -= gap
else:
break
return alist
alist = [3,8,5,7,6,2,1]
print(sort(alist)) # [1, 6, 2, 3, 8, 5, 7]
希尔排序 (最终成型)
# 2.缩减gap
def sort(alist):
gap = len(alist) // 2 #初始增量gap需要放在循环外
while gap >= 1: # 2.缩减gap
for i in range(gap,len(alist)): # 加入增量gap,然后将插入排序代码的中1改为gap
while i>0:
if alist[i] < alist[i-gap]:
alist[i],alist[i-gap] = alist[i-gap],alist[i]
i -= gap
else:
break
gap //= 2 # 2.缩减gap
return alist
alist = [3,8,5,7,6,2,1]
print(sort(alist)) # [1, 2, 3, 5, 6, 7, 8]
快速排序
- 基数:默认情况下,我们将乱序序列的第一个元素作为基数
- 核心:
- 需要将序列中的数值,比基数大的放置在基数右侧,比基数小的放置在基数左侧

# 快速排序
def sort(alist,start,end):
low = start
high = end
if low > high: # 递归结束的条件
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
return
mid = alist[low] # 基数
while low < high: # 让程序继续偏移
while low < high:
if alist[high] > mid: # 让high向左偏移
high -= 1
else:
alist[low] = alist[high]
break
while low < high: # 用来将low向右偏移
if alist[low] < mid:
low += 1
else:
alist[high] = alist[low]
break
if low == high:
alist[low] = mid
# 也可以写成 alist[high] = mid
#递归作用到左侧子序列
sort(alist,start,high-1)
#递归作用到右侧子序列
sort(alist,low+1,end)
return alist
alist = [6,1,2,7,9,3,4,5,10,8]
print(sort(alist,0,len(alist)-1)) # 这里需要传入列表的起始索引
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
更多排序见:



