数据探索性分析（EDA）

数据探索性分析（EDA）

什么是EDA

• 在拿到数据后，首先要进行的是数据探索性分析（Exploratory Data Analysis），它可以有效的帮助我们熟悉数据集、了解数据集。初步分析变量间的相互关系以及变量与预测值之间的关系，并且对数据进行初步处理，如：数据的异常和缺失处理等，以便使数据集的结构和特征让接下来的预测问题更加可靠。
• 并且对数据的探索分析还可以：
  • 1.获得有关数据清理的宝贵灵感（缺失值处理，特征降维等）
  • 2.获得特征工程的启发
  • 3.获得对数据集的感性认识
  • 意义：数据决定了问题能够被解决的最大上限，而模型只决定如何逼近这个上限。

EDA流程

• 1、载入数据并简略观察数据

• 2、总览数据概况
  • 在 describe 中有每一列的统计量、均值、标准差、最小值、中位数25% 50% 75%以及最大值。可以帮助我们快速掌握数据的大概范围和数据的异常判断。
  • 通过 info 来了解每列的 type 和是否存在缺失数据。
  • 通过 isnull().sum() 查看每列缺失情况

• 3、通过 describe 和 matplotlib 可视化查看数据的相关统计量（柱状图）
  • 重点查看方差为0或者极低的特征
    • 数据异常 

• • • 正常值 

• 4、缺失值处理

• 5、查看目标数据的分布
  • 重点查看是否有
    • 分类：类别分布不均衡
      • 可以考虑使用过抽样处理
    • 回归：离群点数据
      • 可以考虑将离群点数据去除
  • 存在着一些特别大或者特别小的值，这些可能是离群点或记录错误点，对我们结果会有一些影响的。那我们是需要将离群点数据进行过滤的。
    • 离群点：离群点是指一个数据序列中，远离序列的一般水平的极端大值和极端小值，且这些值会对整个数据的分析产生异常的影响

• 6、特征分布
  • 绘制数字特征的分布（直方图）
    • 可以观测特征为连续性和还是离散型特征
    • 可以观测特征数值的分布、
    • 是否有离群点 
  • 绘制类别特征的分布（柱状图）
    • 查看该特征中是否有稀疏类，在构建模型时，稀疏类往往会出现问题当然也不是绝对的。如果当前特征比较重要则可以将特征的稀疏类数据删除

　　　　　　　　 

• 7、查看特征于特征之间的相关性（热力图）
  • 相关性强的特征就是冗余特征可以考虑去除。通常认为相关系数大于0.5的为强相关。

• 8、查看特征和目标的相关性，正负相关性越强则特征对结果影响的权重越高，特征越重要。

数据探索性分析（EDA）案例 

数据导入

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
from sklearn.model_selection import train_test_split

data = pd.read_csv('data/Energy_and_Water_Data_Disclosure_for_Local_Law_84_2017__Data_for_Calendar_Year_2016_.csv')
data.head(1)

 

查看数据形状

 

# 查看数据形状
data.shape   # (11746, 60)

查看数据字段类型和是否存在缺失值

 

# 查看数据字段类型和是否存在缺失值
data.info()

数据集中的字段中存有Not Available值，该值表示无效值可以视为缺失值被处理

# 首先将"Not Available"替换为 np.nan 
data = data.replace({'Not Available': np.nan})

数据集有的字段显示为数值型数据，但是实际类型为str，再将部分数值型数据转换成float

 

# 数据集有的字段显示为数值型数据，但是实际类型为str，再将部分数值型数据转换成float
for col in list(data.columns):
    if ('ft²' in col or 'kBtu' in col or 'Metric Tons CO2e' in col or 'kWh' in 
        col or 'therms' in col or 'gal' in col or 'Score' in col):
        data[col] = data[col].astype(float)

通过 describe 和 matplotlib 可视化查看数据的相关统计量（柱状图）

 

data.describe()

# 通过 describe 和 matplotlib 可视化查看数据的相关统计量（柱状图）
data_desc = data.describe() # 查看数据描述
cols = data_desc.columns # 取得列缩影
index = data_desc.index[1:] # 去除count行
plt.figure(figsize=(30, 30))  # 控制画布大小
for i in range(len(cols)):
    ax = plt.subplot(10,6,i+1) # 绘制10x6的表格，当前数据特征维度为60
    ax.set_title(cols[i]) # 设置标题
    for j in range(len(index)):
        plt.bar(index[j], data_desc.loc[index[j], cols[i]]) # 对每个特征绘制describe柱状图
plt.show()
# Order的图形比较正常，因为最小值，中位数，最大值是错落分布，正常分布的，且均值和标准差分布也正常
# DOF Gross Floor Area图形可能有问题，显示最大值比其他的值都大很多(离均点,异常值)，如果最大值的数据数量较少，则考虑将其删除
# 发现：经度，维度特征的std极低，且数值分布特别均匀，说明这俩列特征对结果影响几乎为0，适当考虑过滤该特征

查看每列的缺失值比例

封装查看每列缺失值比例函数（查看每列的缺失值比例，估计大家有很多种方法可以做，可以给大家提供一个函数，把他当做自己的工具吧，以后你会常用到的）

# 查看缺失值
def missing_values_table(df):
        # 计算每一列缺失值的个数
        mis_val = df.isnull().sum(axis=0)
        
        # 计算每列缺失值占该列总数据的百分比
        mis_val_percent = 100 * df.isnull().sum(axis=0) / data.shape[0]
        
        # 将每一列缺失值的数量和缺失值的百分比级联到一起,形成一个新的表格
        mis_val_table = pd.concat([mis_val, mis_val_percent], axis=1)
        
        # 重新给上步表格的列命名
        mis_val_table_ren_columns = mis_val_table.rename(
        columns = {0 : 'Missing Values', 1 : '% of Total Values'})
        
        # 将百分比不为0的行数据根据百分比进行降序排序
        mis_val_table_ren_columns = mis_val_table_ren_columns[
            mis_val_table_ren_columns.iloc[:,1] != 0].sort_values(
        '% of Total Values', ascending=False).round(1)
        
        # 打印概述
        print ("Your selected dataframe has " + str(df.shape[1]) + " columns.\n"      
            "There are " + str(mis_val_table_ren_columns.shape[0]) +
              " columns that have missing values.")
        
        # Return the dataframe with missing information
        return mis_val_table_ren_columns

 

调用函数查看缺失值及比例

missing_df = missing_values_table(data);
missing_df.head(3)

Your selected dataframe has 60 columns.
There are 46 columns that have missing values.

# 下面缺失比例比较大
 

设置阈值将缺失比例超过百分之50的列删除

# 设置阈值将缺失比例超过百分之50的列删除
# 找出超过阈值的列
missing_df = missing_values_table(data);
missing_columns = list(missing_df.loc[missing_df['% of Total Values'] > 50].index)
print('We will remove %d columns.' % len(missing_columns))
data = data.drop(columns = list(missing_columns))

Your selected dataframe has 60 columns.
There are 46 columns that have missing values.
We will remove 11 columns

中位数填充剩下的空值

# 中位数填充剩下的空值 np.median获取中位数，如果原始数据存在空值就会返回空nan
for x in data.columns:
    # 去除object类型的列(object列不存在中位数)
    if str(data[x].dtypes) == 'object':
        continue
    if data[x].isnull().sum() > 0:
        # 取出每列非空元素求得中位数进行填充
        data[x] = data[x].fillna(value=np.median(data.loc[~data[x].isnull(),x]))      

 

 查看目标数据的分布情况

# 查看目标数据的分布情况
data['ENERGY STAR Score'].hist(bins=20)

plt.figure(figsize=(40,20))
plt.scatter(data['ENERGY STAR Score'].index,data['ENERGY STAR Score'].values)
# 由图看到集中到60多出现一条线，说明数据集中在60多，没有找到离群数据
　

data['ENERGY STAR Score'].value_counts().sort_values().tail(1)

65.0    2216
Name: ENERGY STAR Score, dtype: int64

#发现分布在65的数据量是最多的，没有发现离群数据

 

什么是离群点数据？

存在着一些特别大或者特别小的值，这些可能是离群点或记录错误点，对我们结果会有一些影响的。那我们是需要将离群点数据进行过滤的。

• 离群点：离群点是指一个数据序列中，远离序列的一般水平的极端大值和极端小值，且这些值会对整个数据的分析产生异常的影响。
• 传统的过滤方式：
  • Q1 - 3 * IQ：Q1为序列中25%的中位数，IQ为Q3-Q1
  • Q3 + 3 * IQ：Q3为序列中75%的中位数，IQ为Q3-Q1
• 离群点判定：
  • 极小的离群点数据：x < (q1 - 3 * iq)
  • 极大的离群点数据：x > (q3 + 3 * iq)

　　　　

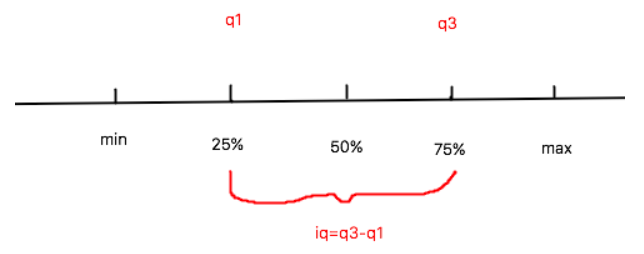
假设我们的目标数据为Site EUI (kBtu/ft²)

寻找离群点

data['Site EUI (kBtu/ft²)'].hist(bins=20)

plt.figure(figsize=(15,8))
plt.scatter(data['Site EUI (kBtu/ft²)'].index,data['Site EUI (kBtu/ft²)'].values)

 离群点数据过滤

# 离群点数据过滤
q1 = data['Site EUI (kBtu/ft²)'].describe()['25%']
q3 = data['Site EUI (kBtu/ft²)'].describe()['75%']
iq = q3 - q1
# data_copy就是离群的数据
data_copy = data[(data['Site EUI (kBtu/ft²)'] > (q1 - 3 * iq)) &
(data['Site EUI (kBtu/ft²)'] < (q3 + 3 * iq))]
# 之后我们就可以对离群点做处理，替换replace还是删除

data_copy['Site EUI (kBtu/ft²)'].hist(bins=30)

plt.scatter(data_copy['Site EUI (kBtu/ft²)'].index,data_copy['Site EUI (kBtu/ft²)'].values)

特征数据的分布

• 可以观测到特征的取值范围
• 可以观测到特征不同数值的分布的密度
• 可以观测到特征是连续性还是离散型

查看特征的不同取值数量

# 查看特征的不同取值数量
for x in data.columns:
    print('*'*50)
    print(x,data[x].nunique())
# 取值少的可能为类别性数据，取值多的为连续性数据

图形查看所有特征数据分布

for col in data.columns:
    if 'int' in str(data[col].dtypes) or 'float' in str(data[col].dtypes):
#         plt.hist(data[col],bins=50)
        sns.distplot(data.loc[~data[col].isnull(),col])
        plt.title(col)
        plt.show()
# 发现有很多特征都是长尾分布的，需要将其转换为正太或者近正太分布，长尾分布说明特征中少数的数值是离群点数据

长尾分布说明特征中少数的数值是离群点数据，需要将其转换为正太或者近正太分布了，log操作转换为近正太分布

log操作转换为近正太分布

# log操作转换为近正太分布
data['DOF Gross Floor Area']
sns.distplot(np.log(data.loc[~data['DOF Gross Floor Area'].isnull(),'DOF Gross Floor Area']))
　

直方图查看数据分布

# 直方图
for col in data.columns:
    if 'int' in str(data[col].dtypes) or 'float' in str(data[col].dtypes):
        plt.hist(data[col],bins=50)
        plt.title(col)
        plt.show()

类别型特征的特征值化

• 结合着项目的目的和对非数值型字段特征的理解等手段，我们只选取出两个代表性特征Borough和Largest Property Use Type对其进行onehot编码实现特征值化

features = data.loc[:,data.columns != 'ENERGY STAR Score']# 提取特征数据
fea_name = features.select_dtypes('number').columns # 提取数值型特征名称
features = features[fea_name] # 提取数值型特征
# 提取指定的两个类别型特征
categorical_subset = data[['Borough', 'Largest Property Use Type']]
categorical_subset = pd.get_dummies(categorical_subset)
features = pd.concat([features, categorical_subset], axis = 1)

探索特征之间的相关性

• 　　corr查看特征与特征的相关性

features.corr() # corr查看特征与特征的相关性


plt.subplots(figsize=(30,15)) #指定窗口尺寸（单位英尺）
features_corr=features.corr().abs() # 返回列与列之间的相关系数 abs求得是绝对值，相关系数与正负无关
# 数据为相关系数，显示数值，显示颜色条 这里需要导入模快 import seaborn as sns 也是一个绘图模块
sns.heatmap(features_corr, annot=True)
　

去除相关性强的冗余特征，工具包封装如下

cols = features.columns # 获取列的名称
corr_list = []
size = features.shape[1]
high_corr_fea = [] # 存储相关系数大于0.5的特征名称
for i in range(0,size):
    for j in range(i+1, size):
        if(abs(features_corr.iloc[i,j])>= 0.5):
            corr_list.append([features_corr.iloc[i,j], i, j]) # features_corr.iloc[i,j]：按位置选取数据
                      
sorted_corr_list = sorted(corr_list, key=lambda xx:-abs(xx[0]))
# print(sorted_corr_list)
for v,i,j in sorted_corr_list:
    high_corr_fea.append(cols[i])
    print("%s and %s = %.2f" % (cols[i], cols[j],v)) # cols: 列名 

删除相关性强的特征

# 删除特征
features.drop(labels=high_corr_fea,axis=1,inplace=True)

features.shape  # (11746, 69)

查看特征和目标之间的相关性

• 如果特征和标签之间是存在线性关系的才可以采用如下方式

target = data['ENERGY STAR Score']
target = pd.DataFrame(data=target,columns=['ENERGY STAR Score'])
# 级联target&features
new_data = pd.concat((features,target),axis=1)

# 计算相关性,之后我们就可以选择特征与目标相关性较大的数据进行特征的选取
fea_target_corr = abs(new_data.corr()['ENERGY STAR Score'][:-1])
fea_target_corr 

保存数据

# 改名字
new_data = new_data.rename(columns = {'ENERGY STAR Score': 'score'})

new_data.to_csv('./data/eda_data.csv')

建模 (该案例是回归问题)

数据集导入及切分

# Pandas and numpy for data manipulation
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
import seaborn as sns
from sklearn.preprocessing import MinMaxScaler
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestRegressor
from sklearn.svm import SVR
from sklearn.neighbors import KNeighborsRegressor
from lightgbm import LGBMRegressor
# Hyperparameter tuning
from sklearn.model_selection import GridSearchCV,train_test_split

data = pd.read_csv('./data/eda_data.csv').drop(labels='Unnamed: 0',axis=1)

fea_name = [x for x in data.columns if x not in ['score']]

feature = data[fea_name]
target = data['score']

x_train,x_test,y_train,y_test = train_test_split(feature,target,test_size=0.2,random_state=2020)

选择的机器学习算法（回归问题）

1. Linear Regression
2. Support Vector Machine Regression
3. Random Forest Regression
4. lightGBM (忽略)
5. xgboost
   • 我们只选择其默认的参数，这里先不进行调参工作，后续再来调参。

• 由于模型的调用和评价方式是一样的，则封装如下工具函数

# Function to calculate mean absolute error
def mae(y_true, y_pred):
    return np.mean(abs(y_true - y_pred))

# Takes in a model, trains the model, and evaluates the model on the test set
def fit_and_evaluate(model):
    
    # Train the model
    model.fit(x_train, y_train)
    
    # Make predictions and evalute
    model_pred = model.predict(x_test)
    model_mae = mae(y_test, model_pred)
    
    # Return the performance metric
    return model_mae

尝试各种模型

# 线性回归
lr = LinearRegression()
lr_mae = fit_and_evaluate(lr)

print('Linear Regression Performance on the test set: MAE = %0.4f' % lr_mae)

Linear Regression Performance on the test set: MAE = 20.8585

# svm支向量机
svm = SVR(C = 1000, gamma = 0.1)
svm_mae = fit_and_evaluate(svm)

print('Support Vector Machine Regression Performance on the test set: MAE = %0.4f' % svm_mae)

Support Vector Machine Regression Performance on the test set: MAE = 21.3965

# 随机森林
random_forest = RandomForestRegressor(random_state=60)
random_forest_mae = fit_and_evaluate(random_forest)

print('Random Forest Regression Performance on the test set: MAE = %0.4f' % random_forest_mae)

Random Forest Regression Performance on the test set: MAE = 11.7919

条形图显示mae

plt.style.use('fivethirtyeight')
model_comparison = pd.DataFrame({'model': ['Linear Regression', 'Support Vector Machine',
                                           'Random Forest',
                                            ],
                                 'mae': [lr_mae, svm_mae, random_forest_mae,]})
model_comparison.sort_values('mae', ascending = False).plot(x = 'model', y = 'mae', kind = 'barh',
                                                           color = 'red', edgecolor = 'black')
plt.ylabel(''); plt.yticks(size = 14); plt.xlabel('Mean Absolute Error'); plt.xticks(size = 14)
plt.title('Model Comparison on Test MAE', size = 20)

看起来集成算法更占优势一些，这里存在一些不公平，因为参数只用了默认，但是对于SVM来说参数可能影响会更大一些。

模型调参 (这里用网格搜索找寻最佳参数)

• 以随机森林参数调优为例

from sklearn.model_selection import GridSearchCV

parameters = {
              'n_estimators':[150,200,250]
              ,'min_samples_split':[2, 3, 5, 10, 15]
              ,"max_depth":[2, 3, 5, 10, 15]
              ,'min_samples_leaf':[1, 2, 4, 6, 8]
              ,'min_samples_split':[2, 4, 6, 10]
}
model = RandomForestRegressor()
GS = GridSearchCV(estimator=model,param_grid=parameters,cv=5,scoring='neg_mean_absolute_error')
GS.fit(x_train,y_train)
GS.best_params_