Codeforces 杂题集
记录一些没有写在其他随笔中的 Codeforces 杂题, 以 Problemset 题号排序
欧拉序, 线段树
//给个图, 两种操作, 查询一个点所在联通块的最大值并改为0; 删边
//离线操作, 倒着做. 线段树维护欧拉序. 要注意的一点是, 如何求一个点在删一部分边后的祖先, 我们倒着操作时用并查集维护关系, 保存该点当时在并查集里的祖先即可
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define inc(i, l, r) for (int i = l; i <= r; i++)
#define dec(i, l, r) for (int i = l; i >= r; i--)
#define pii pair<int, int>
#define fi first
#define se second
#define pb push_back
const int maxn = 4e5 + 5;
const int maxm = 3e5 + 5;
const int maxq = 5e5 + 5;
int N, M, Q;
int par[maxn];
void init(int n) { inc(i, 1, n) par[i] = i; }
int find(int x) {
if (x == par[x]) return x;
return par[x] = find(par[x]);
}
bool same(int x, int y) { return find(x) == find(y); }
struct edge {
int u, v, id;
} e[maxm];
int vis[maxm], root[maxm + maxq], vis_point[maxn];
vector<int> g[maxn];
int euler[2 * maxn], in[maxn], out[maxn], top;
int a[maxn], mx[8 * maxn], pos[8 * maxn];
void dfs(int x) {
vis_point[x] = 1;
in[x] = ++top;
if (x <= N) euler[top] = a[x];
for (int son : g[x]) {
if (!vis_point[son]) dfs(son);
}
out[x] = ++top;
}
void up(int k) {
mx[k] = max(mx[k << 1], mx[k << 1 | 1]);
if (mx[k << 1] >= mx[k << 1 | 1])
pos[k] = pos[k << 1];
else
pos[k] = pos[k << 1 | 1];
}
void build(int k, int l, int r) {
if (l == r) {
mx[k] = euler[l];
pos[k] = l;
return;
}
int mid = l + r >> 1;
build(k << 1, l, mid);
build(k << 1 | 1, mid + 1, r);
up(k);
}
pii query(int k, int l, int r, int a, int b) { //返回最大值及其位置
if (a <= l && r <= b) {
return pii(mx[k], pos[k]);
}
int mid = l + r >> 1;
pii res = pii(0, 0);
if (a <= mid) res = max(res, query(k << 1, l, mid, a, b));
if (b > mid) res = max(res, query(k << 1 | 1, mid + 1, r, a, b));
return res;
}
void change(int k, int l, int r, int pos) {
if (l == r) {
mx[k] = 0;
return;
}
int mid = l + r >> 1;
if (pos <= mid)
change(k << 1, l, mid, pos);
else
change(k << 1 | 1, mid + 1, r, pos);
up(k);
}
int main() {
scanf("%d %d %d", &N, &M, &Q);
inc(i, 1, N) scanf("%d", &a[i]);
inc(i, 1, M) {
scanf("%d %d", &e[i].u, &e[i].v);
e[i].id = i;
}
vector<pii> q;
while (Q--) {
int op, x;
scanf("%d %d", &op, &x);
q.push_back(pii(op, x));
if (op == 2) vis[x] = 1;
}
inc(i, 1, M) if (!vis[i]) q.push_back(pii(2, i));
init(2 * N);
int cnt = N;
dec(i, (int)q.size() - 1, 0) {
if (q[i].fi == 1) {
root[i] = find(q[i].se); //询问i的祖先
// cout << "root " << i << " " << root[i] << "\n";
} else {
int p = q[i].se;
if (!same(e[p].u, e[p].v)) {
++cnt;
g[cnt].push_back(par[e[p].u]), g[cnt].push_back(par[e[p].v]);
par[par[e[p].u]] = cnt, par[par[e[p].v]] = cnt;
}
}
}
inc(i, 1, cnt) if (!vis_point[find(i)]) dfs(find(i));
build(1, 1, top);
inc(i, 0, (int)q.size() - 1) {
if (q[i].fi == 1) {
int l = in[root[i]], r = out[root[i]];
pii res = query(1, 1, top, l, r);
cout << res.fi << "\n";
change(1, 1, top, res.se);
}
}
}
图的转换
// m个集合, 对于每个集合i里的x<y, x与y连颜色为i的边
//每个集合有权值a_i,数字有权值b_i
//现在要用最小的代价删去某些集合里的某些数, 使最后图里没有 颜色各不相同的环
//最后图里没有颜色各不相同的环, 等价于, 建立一个二分图, 左边集合1-m右边点1-n,
//集合i有啥就和右边的数字连边, 最后二分图里没有环
//二分图边(i,j)的权值为a[i]+b[j], 跑最大生成树, 不要的边就是从那个集合里删掉的数
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define inc(i, l, r) for (int i = l; i <= r; i++)
const int maxn = 1e6 + 5;
int n, m, sz, x;
int a[maxn], b[maxn];
struct edge {
int u, v, len;
};
vector<edge> g;
int par[maxn];
void init() { inc(i, 1, n + m) par[i] = i; }
int find(int x) {
if (par[x] == x) return x;
return par[x] = find(par[x]);
}
void unite(int x, int y) { par[find(x)] = find(y); }
bool same(int x, int y) { return find(x) == find(y); }
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> m >> n;
inc(i, 1, m) cin >> a[i];
inc(i, 1, n) cin >> b[i];
inc(i, 1, m) {
cin >> sz;
inc(j, 1, sz) {
cin >> x;
g.push_back({i, m + x, a[i] + b[x]});
}
}
sort(g.begin(), g.end(), [&](edge u, edge v) { return u.len > v.len; });
ll res = 0;
init();
for (auto e : g) {
if (same(e.u, e.v))
res += e.len;
else
unite(e.u, e.v);
}
cout << res << "\n";
}
构造
//函数 f 输入两个数 返回一个数
//起始序列1-n, 要求构造q组操作, 每次都选出两个位置的数x,y, 用f(x,y)代替他们
//使得最后序列里只有至多两种值. 对于所有可能的 f 都是成立的.
//比较好构造出区间长 len=2^x 的元素全部一致的方案,
//然后对[1,len]和[n-len+1,n]的区间操作一下最多就只有两种值了
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define inc(i, l, r) for (int i = l; i <= r; i++)
#define dec(i, l, r) for (int i = l; i >= r; i--)
#define pii pair<int, int>
#define fi first
#define se second
#define pb push_back
const int maxn = 1e6 + 5;
int n, top;
pii p[maxn];
void out(int x, int y) { p[top++] = pii(x, y); }
int main() {
cin >> n;
int m = 1 << (int)log2(n);
for (int i = 1; i <= m / 2; i <<= 1) {
for (int j = 1, k = 0; j <= m; k++) {
out(j + k, j + k + i);
if (k == i - 1) k = -1, j += 2 * i;
}
}
for (int i = 1; i <= m / 2; i <<= 1) {
for (int j = 1, k = 0; j <= m; k++) {
out(j + k + n - m, j + k + i + n - m);
if (k == i - 1) k = -1, j += 2 * i;
}
}
cout << top << "\n";
inc(i, 0, top - 1) cout << p[i].fi << " " << p[i].se << "\n";
}
下标的妙用, 线段树
//对一个数组有4种操作, 单点修改, reverse[(i−1)*2^k+1,i*2^k],
// swap [(2i−2)*2k+1,(2i−1)*2k] 和 [(2i−1)2^k+1,2i*2^k], 区间求和, n<=1e5
// reverse视为下标异或(1<<k)-1, swap视为下标异或1<<k.
// 区间查询时把区间分成若干个份, 每一份都是从xxx000-xxx111的形式.
// 这里我采用枚举合适的(1<<i)-1作为区间值,保证区间最多分为logn份,
// 然后这个区间的下标异或偏移量之后仍是xxx000-xxx111的形式,在线段树中查询即可
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define inc(i, l, r) for (int i = l; i <= r; i++)
const int maxn = (1 << 18) + 5;
int N, n, q, x, k, delta;
ll w[4 * maxn];
void build(int k, int l, int r) {
if (l == r) {
scanf("%lld", &w[k]);
return;
}
int m = l + (r - l) / 2;
build(2 * k, l, m);
build(2 * k + 1, m + 1, r);
w[k] = w[2 * k] + w[2 * k + 1];
}
void change1(int k, int l, int r, int pos, int val) {
if (l == r) {
w[k] = val;
return;
}
int m = l + r >> 1;
if (pos <= m)
change1(2 * k, l, m, pos, val);
else
change1(2 * k + 1, m + 1, r, pos, val);
w[k] = w[2 * k] + w[2 * k + 1];
}
ll ask2(int k, int l, int r, int a, int b) {
if (a <= l && r <= b) return w[k];
ll res = 0;
int m = l + r >> 1;
if (a <= m) res += ask2(2 * k, l, m, a, b);
if (b > m) res += ask2(2 * k + 1, m + 1, r, a, b);
return res;
}
int main() {
scanf("%d %d", &n, &q);
build(1, 0, (1 << n) - 1);
while (q--) {
cin >> x;
if (x == 1) {
scanf("%d %d", &x, &k);
x--;
change1(1, 0, (1 << n) - 1, x ^ delta, k);
} else if (x == 2) {
scanf("%d", &k);
delta ^= (1 << k) - 1;
} else if (x == 3) {
scanf("%d", &k);
delta ^= 1 << k;
} else {
scanf("%d %d", &x, &k);
x--, k--;
ll res = 0;
for (int l = x; l <= k;) {
inc(d, 1, n + 1) {
if (l + (1 << d) - 1 > k || (l & ((1 << d) - 1)) != 0) {
d--;
int D = (1 << d) - 1;
int cl = l ^ (delta & ~D);
res += ask2(1, 0, (1 << n) - 1, cl, cl + D);
l += 1 << d;
break;
}
}
}
printf("%lld\n", res);
}
}
}
题意: 一个矩形的每一行被分成若干个区间, 每个区间可以选个位置填 1, 其余是 0; 要最大化每一列的平方和.
题解: \(dp_{l,r}\) 为考虑那些区间完全在 \([l,r]\) 内的贡献的情况下的最大答案, 每次转移时枚举中间的间隔 \(k\). (一种错解:)不能 \(dp_{l,r}\) 为前 \(i\) 列还有 \(j\) 个区间没有填 1, 因为这样没有存储这 \(j\) 个区间在哪里结束的信息, 会多算情况.
view code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define inc(i, l, r) for (int i = l; i <= r; i++)
const int maxn = 105;
int n, m, k, u, v, z[maxn][maxn], y[maxn][maxn];
int a[maxn][maxn], dp[maxn][maxn];
int solve(int l, int r) {
if (l > r) return 0;
if (dp[l][r] != -1) return dp[l][r];
inc(k, l, r) {
int tmp = solve(l, k - 1) + solve(k + 1, r), cnt = 0;
inc(i, 1, n) if (z[i][k] >= l && y[i][k] <= r) cnt++;
dp[l][r] = max(dp[l][r], tmp + cnt * cnt);
}
return dp[l][r];
}
int main() {
cin >> n >> m;
inc(i, 1, n) {
cin >> k;
inc(j, 1, k) {
cin >> u >> v;
inc(l, u, v) z[i][l] = u, y[i][l] = v;
}
}
inc(i, 1, m) inc(j, 1, m) dp[i][j] = -1;
printf("%d\n", solve(1, m));
}
题意: 给出一个 1 - n 的排列 \({p_i}\), 某些位置有"炸弹"(但至少有一个位置没有炸弹), 按顺序扫描一遍 \({p_i}\), 每扫到一个数就把它加入集合, 如果该位置有炸弹, 就移除当前集合中最大的数, 最后输出集合中最大的数作为结果. 有另一个排列 \({q_i}\), 假设当前 i = x, 则位置 \(q_1, q_2, ... , q_{x-1}\) 是有炸弹的. 输出 i 取遍 1 - n 的答案. n ≤ 3e5.
思路: 我们只关心当前最大的数是否会被炸弹带走, 例如初始最大的数是 n, 只要当前所有炸弹都在 n 的前面, 答案就一直是 n; 当 n 被炸没了, 就考虑 n - 1 能否成为答案, 依此类推. 所以我们要快速查询对于一个数是否会被炸弹带走, 假设对于当前的数 now 后面有 x 个炸弹, 而前面有 y 个比 now 大的数没有被炸掉, 当 y ≥ x 时说明 now 没有被炸掉. 考虑这样的一个序列, 当出现一个炸弹时, 对应位置 -1, 而当前已出现的数(从大往小枚举)所在位置 +1, 如果该序列的一个后缀和为正数(并且后缀和的位置一定要包括到 pos[now]), 代表比 now 大的数不比炸弹少(事实上只会小于等于), now 就是答案; 否则 now 自减 1, now 自减后所在的位置 +1, 继续查询它的后缀和是否为正. 用线段树维护这个序列的后缀和即可.
view code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define inc(i, l, r) for (int i = l; i <= r; i++)
const int maxn = 3e5 + 5;
int p[maxn], q[maxn], n, pos[maxn];
int c[maxn];
int f[maxn * 4], mx[maxn * 4];
void down(int k, int l, int r) {
if (f[k]) {
int mid = l + r >> 1;
f[k << 1] += f[k], mx[k << 1] += f[k];
f[k << 1 | 1] += f[k], mx[k << 1 | 1] += f[k];
f[k] = 0;
}
}
void up(int k) { mx[k] = max(mx[k << 1], mx[k << 1 | 1]); }
void add(int k, int l, int r, int a, int b, int val) {
if (a <= l && r <= b) {
f[k] += val;
mx[k] += val;
return;
}
down(k, l, r);
int mid = l + r >> 1;
if (a <= mid) add(k << 1, l, mid, a, b, val);
if (b > mid) add(k << 1 | 1, mid + 1, r, a, b, val);
up(k);
}
int query(int k, int l, int r, int a, int b) {
if (a <= l && r <= b) return mx[k];
down(k, l, r);
int res = 0;
int mid = l + r >> 1;
if (a <= mid) res = max(res, query(k << 1, l, mid, a, b));
if (b > mid) res = max(res, query(k << 1 | 1, mid + 1, r, a, b));
return res;
}
int main() {
scanf("%d", &n);
inc(i, 1, n) {
scanf("%d", &p[i]);
pos[p[i]] = i;
}
inc(i, 1, n) scanf("%d", &q[i]);
int now = n;
add(1, 1, n, 1, pos[now], 1);
inc(i, 1, n) {
printf("%d%c", now, i == n ? '\n' : ' ');
if (i == n) break;
add(1, 1, n, 1, q[i], -1);
while (query(1, 1, n, 1, pos[now]) <= 0) {
now--;
add(1, 1, n, 1, pos[now], 1);
}
}
}
1325E - Ehab's REAL Number Theory Problem
题意: 给出 n 个数 ai, n ≤ 1e5, 1 ≤ ai ≤ 1e6, ai 最多有 7 个因子. 要选出一个非空的子序列, 使得这些数的积是一个完全平方数. 问子序列的最短长度.
思路: 每个数选取后至多影响到积的 2 个质因子的奇偶性, 因此可以对每一个数建边: 有 2 个次数为奇数的质因子时连接代表这两个数的节点; 只有 1 个次数为奇数的质因子时连接该数与 1; 否则, 该数就是一个完全平方数. 建图后相当于要选出一个最小子图, 每个点的度数是偶数, 问题便转换为找到图上最小的环, 这个图最多有 1e5个点. 考虑朴素的做法: 对每一个节点 bfs, 可以找到该点所在的最小环. 复杂度为 \(O(n^2)\). 注意到大于 \(\sqrt n\) 的两个数间不会建边, 即所有环一定经过了不大于 \(\sqrt n\) 的质数或点 1 (最多 169 个节点). 这样可以只 bfs 这些节点更新答案.
view code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define inc(i, l, r) for (int i = l; i <= r; i++)
const int maxn = 1e5 + 5;
const int maxnum = 1e6;
int prim[maxnum], pvis[maxnum + 5], pcnt, id[maxnum + 5];
void getprim() {
for (int i = 2; i <= maxnum; i++) {
if (!pvis[i]) {
prim[++pcnt] = i;
id[i] = pcnt;
}
for (int j = 1; j <= pcnt && prim[j] * i <= maxnum; j++) {
pvis[prim[j] * i] = 1;
if (i % prim[j] == 0) break;
}
}
}
int n, a[maxn], res;
vector<int> g[maxn];
void con(int u, int v) {
g[u].push_back(v);
g[v].push_back(u);
}
int d[maxn];
void bfs(int s) {
memset(d, 127, sizeof(d));
queue<int> que;
que.push(s);
d[s] = 0;
while (que.size()) {
int q = que.front();
que.pop();
for (int i : g[q]) {
if (d[i] == d[q] + 1 || d[i] == d[q]) {
res = min(res, d[i] + d[q] + 1);
return;
} else if (d[i] > d[q] + 1) {
d[i] = d[q] + 1;
que.push(i);
}
}
}
}
int main() {
getprim();
res = 10'000'000;
scanf("%d", &n);
inc(i, 0, n - 1) scanf("%d", &a[i]);
inc(i, 0, n - 1) {
vector<int> v;
for (int j = 1; j <= 168; j++) {
if (a[i] % prim[j] == 0) {
int cnt = 0;
while (a[i] % prim[j] == 0) {
cnt++;
a[i] /= prim[j];
}
if (cnt & 1) v.push_back(j);
}
}
if (a[i] > 1) v.push_back(id[a[i]]);
if (v.size() == 2)
con(v[0], v[1]);
else if (v.size() == 1)
con(v[0], 0);
else {
res = 1;
break;
}
}
for (int i = 0; i <= 168; i++) bfs(i);
if (res == 10'000'000) res = -1;
cout << res << "\n";
}
题意: 给出一个 n 个点, m 条边的图, n ≤ 1e5, m ≤ 2e5, 没有重边, 自环. 要求输出它的一个大小为 \(\lceil n \rceil\) 的独立集或者长度至少为 \(\lceil n \rceil\) 的环(自行选择并可证明一定有解).
思路: 官方题解给出了一个很有意义的定理: 图上所有节点的度数都不小于 d 时, 图上一定存在一个长度不小于 d + 1 的环. 证明: 从任意一点 dfs 直至当前 dfs 的点的相邻点都已被标记, 由于它的度数不小于 d, 说明当前 dfs 链上已有至少 d + 1 个点, 令当前点与它的相邻点中最接近 dfs 序的起点的点连接便构成了需要的环. 回到原题, 我们不断地删除图上度数小于 \(\lceil n \rceil - 1\) 的点及其相邻点, 如果能以此法进行 \(\lceil n \rceil\) 次, 便找到了需要的独立集; 如果在某一时刻找不到度数小于 \(\lceil n \rceil\) 的点, 便可以运用前述定理找到需要的环(此时剩余的子图一定不为空).
view code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define inc(i, l, r) for (int i = l; i <= r; i++)
const int maxn = 1e5 + 5;
int n, m, u, v, sq;
vector<int> g[maxn];
int du[maxn], vis[maxn], vis2[maxn], vis3[maxn];
vector<int> r1, r2;
int cnt;
void dfs(int x) {
vis2[x] = 1;
r2.push_back(x);
int fail = 1;
for (int i : g[x]) {
if (!vis[i] && !vis2[i]) {
fail = 0;
dfs(i);
// break;
}
}
if (fail) {
cout << "2\n";
for (int i : g[x]) vis3[i] = 1;
vis3[x] = 1;
int sz = r2.size();
inc(i, 0, sz - 1) if (vis3[r2[i]]) {
cout << sz - i << "\n";
inc(j, i, sz - 1) cout << r2[j] << " ";
break;
}
cout << "\n";
exit(0);
}
}
int main() {
scanf("%d %d", &n, &m);
for (int i = 1; i <= m; i++) {
scanf("%d %d", &u, &v);
g[u].push_back(v);
g[v].push_back(u);
du[u]++, du[v]++;
}
sq = (int)ceil(sqrt(n));
inc(i, 1, sq) {
inc(j, 1, n) if (!vis[j] && du[j] < sq - 1) {
r1.push_back(j);
vis[j] = 1;
for (int k : g[j]) {
if (!vis[k]) {
vis[k] = 1, du[k]--;
for (int l : g[k]) du[l]--;
}
}
break;
}
if (r1.size() < i) break;
if (i == sq) {
cout << "1\n";
for (int j : r1) cout << j << " ";
cout << "\n";
return 0;
}
}
inc(i, 1, n) {
if (!vis[i]) {
dfs(i);
break;
}
}
}
题意: 为了组建排球队, 现在需要 p 个选手和 k 个观众, 给出 n 个人选, 每个人具有去做第 j 位选手和观众贡献的力量值 \(s_{ij}\) 和 \(a_i\). 现在要最大化总力量值. 2 ≤ n ≤ 1e5, 1 ≤ p ≤ 7, 1 ≤ k, p + k ≤ n.
思路: 按 \(a_i\) 降序排序, 定义 dp[i][S] 为使用前 i 个人时的最大力量值(每个人做选手, 观众, 或什么也不做都有可能), S 是位置被占用的状态. 状态转移时, 考虑第 i 个人: 1. 做第 j 位选手; 2. 做观众; 3. 吃瓜. (1) (3) 都是好做的, 而做观众得考虑当前当观众的机会是否已经用完了. 由于已经按 \(a_i\) 降序排序, 所以观众总是贪心地取前面的未做选手的人, 所以对于 dp[i][S] 做观众的人数为 max(i - popcount(S), k), 即靠前的人不当选手就得当观众, 这样就可以知道当前第 i 人能否还能当观众.
view code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define inc(i, l, r) for (int i = l; i <= r; i++)
const int maxn = 1e6 + 5;
int n, k, p;
ll dp[2][130];
int s[maxn][10], a[maxn], id[maxn];
bool cmp(int x, int y) { return a[x] > a[y]; }
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> p >> k;
inc(i, 0, n - 1) cin >> a[i];
inc(i, 0, n - 1) inc(j, 0, p - 1) cin >> s[i][j];
inc(i, 0, n - 1) id[i] = i;
sort(id, id + n, cmp);
ll *now = dp[0], *nxt = dp[1];
inc(j, 1, (1 << p) - 1) nxt[j] = -1;
inc(i, 0, n - 1) {
inc(j, 0, (1 << p) - 1) now[j] = nxt[j];
inc(j, 0, (1 << p) - 1) {
if (now[j] == -1) continue;
inc(k, 0, p - 1) if (!((j >> k) & 1)) nxt[j | (1 << k)] =
max(nxt[j | (1 << k)], now[j] + s[id[i]][k]);
if (i - __builtin_popcount(j) < k) {
nxt[j] = max(nxt[j], now[j] + a[id[i]]);
}
}
}
cout << nxt[(1 << p) - 1] << "\n";
}
1313C2 - Skyscrapers (hard version)
题意: 给出N个摩天大楼的最大高度, 要求高度数列是山脊型, 问最大的高度和.
思路: 感觉像 \(dp\). 但是这题每个数只减不增, 所以在确定某一点为最大时, 其他点的答案是唯一确定的(贪心). 从两边各扫描一遍单调栈处理出\(\sum_{1≤j≤i}h_j\)和\(\sum_{i≤j≤n}h_j\)的最大值.
view code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define inc(i, l, r) for (int i = l; i <= r; i++)
#define dec(i, l, r) for (int i = l; i >= r; i--)
const int maxn = 1e6 + 5;
int a[maxn];
ll pre[maxn], suff[maxn];
int n;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
inc(i, 0, n - 1) cin >> a[i];
stack<int> id;
ll sum = 0;
inc(i, 0, n - 1) {
while (!id.empty() && a[i] < a[id.top()]) {
int j = id.top();
id.pop();
sum -= (ll)a[j] * (j - (id.empty() ? -1 : id.top()));
}
sum += (ll)a[i] * (i - (id.empty() ? -1 : id.top()));
pre[i] = sum;
id.push(i);
}
while (id.size()) id.pop();
sum = 0;
dec(i, n - 1, 0) {
while (!id.empty() && a[i] < a[id.top()]) {
int j = id.top();
id.pop();
sum -= (ll)a[j] * ((id.empty() ? n : id.top()) - j);
}
sum += (ll)a[i] * ((id.empty() ? n : id.top()) - i);
pre[i] += sum;
id.push(i);
}
inc(i, 0, n - 1) pre[i] -= a[i];
int pos = max_element(pre, pre + n) - pre;
dec(i, pos - 1, 0) if (a[i] > a[i + 1]) a[i] = a[i + 1];
inc(i, pos + 1, n - 1) if (a[i] > a[i - 1]) a[i] = a[i - 1];
inc(i, 0, n - 1) cout << a[i] << " ";
cout << "\n";
}
题意: 给出一个有 n 个数的数列 \(a_i\), 可以选择两个大小相同位置相邻的数 x, 用一个 x + 1 代替这两个元素. 问数列经任意次合并后的最短长度. n ≤ 100, \(1 ≤ a_i ≤ 1000\).
思路: \(dp[l][r]\) 为区间 [l, r] 能否合并成一个元素, 若不能则返回 -1, 若可以则返回最后合并的结果. 状态转移时, 考虑到如果一个长度大于 1 的区间可以合并成一个元素, 那它一定可以分成两个也可以合并成一个元素的区间(并且大小相同).
view code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define inc(i, l, r) for (int i = l; i <= r; i++)
const int maxn = 1e3 + 5;
int n, a[maxn], dp[maxn][maxn];
int f[maxn];
int solve(int l, int r) {
if (dp[l][r] != 0) return dp[l][r];
inc(i, l, r - 1) {
int pre = solve(l, i);
if (pre != -1 && pre == solve(i + 1, r)) return dp[l][r] = pre + 1;
}
return dp[l][r] = -1;
}
int main() {
cin >> n;
inc(i, 1, n) cin >> a[i];
inc(i, 1, n) dp[i][i] = a[i];
inc(i, 1, n) {
f[i] = n;
inc(j, 1, i) {
if (solve(j, i) > 0) f[i] = min(f[i], f[j - 1] + 1);
}
}
cout << f[n] << "\n";
}
1311E - Construct the Binary Tree
题意: 构造一个 n 个点深度和为 d 的二叉树.
思路: 链状的树深度和是最大的, 以此为初始状态, 每次把最下面的节点往上移至某一层填满或者深度和达到 d. 这也说明了 n 固定时深度和是在一个区间上连续的. 知道每层有几个点后, 层序遍历输出顶点.
view code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define inc(i, l, r) for (int i = l; i <= r; i++)
const int maxn = 3e5 + 5;
const int inf = 0x3f3f3f3f;
int l[maxn], r[maxn];
int main() {
int t, n, d;
inc(i, 2, 5000) {
l[i] = inf;
inc(j, 0, i - 1) {
l[i] = min(l[j] + l[i - j - 1] + i - 1, l[i]);
r[i] = max(r[j] + r[i - j - 1] + i - 1, r[i]);
}
}
cin >> t;
while (t--) {
cin >> n >> d;
if (d < l[n] || d > r[n]) {
cout << "NO\n";
continue;
}
cout << "YES\n";
vector<int> v(n, 1);
int tmp = n * (n - 1) / 2, last = 1, top = n - 1;
while (tmp > d) {
if (tmp - (top - last) >= d) {
tmp -= top - last;
if (--v[top] == 0) top--;
if (last < 30 && ++v[last] == 1 << last) last++;
} else {
v[top]--;
v[top - (tmp - d)]++;
break;
}
}
int cnt = 1;
for (int i = 1; i <= n - 1 && v[i]; i++) {
inc(j, 0, v[i] - 1) { cout << cnt + j / 2 << " "; }
cnt += v[i - 1];
}
cout << "\n";
}
}
题意: 给出一个N(N \(\leq\) 2e5)个点的无向图, 已知其中有k(2 \(\leq\) k \(\leq\) N)个点是"特殊的"的, 你必须选择其中两个点连边, 使得点1到点N的距离最大化.
思路: 问题转化为最大化 min(d[1][u] + 1 + d[v][n], d[1][v] + 1 + d[u][n]). 此时是希望在固定i/j时可以确定min取哪个. 按d[1][u] - d[u][n]降序排列, 此时在选定当前点 i 后, 另一个点 j (j > i)无论是哪个, 最小值都是d[1][i] + 1 + d[j][n], 利用这一点, 就可以O(1)地查询后缀解决.
view code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define inc(i, l, r) for (int i = l; i <= r; i++)
#define pii pair<int, int>
#define fi first
#define se second
#define pb push_back
int n, m, k;
const int maxv = 2e5 + 5;
const int inf = 0x3f3f3f3f;
int V, d[maxv];
vector<int> g[maxv];
pii p[maxv];
int suffix[maxv];
void solve(int s) {
queue<int> que;
que.push(s);
memset(d, 63, sizeof(d));
d[s] = 0;
while (!que.empty()) {
int q = que.front();
que.pop();
for (int i = 0; i < g[q].size(); i++) {
if (d[g[q][i]] == inf) {
d[g[q][i]] = d[q] + 1;
que.push(g[q][i]);
}
}
}
}
bool cmp(const pii &p1, const pii &p2) { return p1.fi - p1.se < p2.fi - p2.se; }
int sp[maxv], u, v;
int main() {
cin >> n >> m >> k;
inc(i, 0, k - 1) cin >> sp[i];
inc(i, 1, m) {
u--, v--;
cin >> u >> v;
g[u].pb(v);
g[v].pb(u);
}
solve(1);
for (int i = 0; i < k; i++) p[i].fi = d[sp[i]];
solve(n);
for (int i = 0; i < k; i++) p[i].se = d[sp[i]];
sort(p, p + k, cmp);
suffix[k - 1] = p[k - 1].se;
for (int i = k - 2; i >= 0; i--) suffix[i] = max(suffix[i + 1], p[i].se);
int res = 0;
for (int i = 0; i < k - 1; i++) res = max(res, p[i].fi + suffix[i + 1] + 1);
cout << min(d[1], res);
}
题意: 给出一列N个草的美味程度, 现在有M只牛, 牛会从左端或右端出发, 见到与自己fi相同的草就吃, 吃满hi单位的草为止, 然后原地倒下, 不让其他牛经过自己. 农夫要选出尽可能多的牛吃草, 而不发生有牛被吃饱了倒下的其他牛挡到的情况. 问最大的牛数量以及方案数(左边出发还是右边出发认为是不同的, 出发的顺序是不考虑的). N≤5000, M≤5000.
思路: 杜老师说这是道狗 shi 题. 只能想到以dp[i][j]为当前从左出发的牛最远到i, 从右出发到j. 正解是考虑枚举从左边出发的牛最远到哪, 然后就可以考虑吃各种美味程度的牛都会产生怎样的贡献. 注意不要漏掉从左出发到 0 的情况. 另外我自己的方法是确保有牛到达这个最远的地方(也导致讨论的情况变多), 不然可能会重复算方案数. 这题O(n^2)维护的变量是可以优化到 O(nlogn) 的.
view code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define inc(i, l, r) for (int i = l; i <= r; i++)
#define dec(i, l, r) for (int i = l; i >= r; i--)
const int maxn = 5e3 + 5;
const int mod = 1e9 + 7;
int n, m, t, f;
int a[maxn], pre[maxn];
int ans1[maxn];
ll ans2[maxn];
int top[maxn];
struct cow {
int f, l, r;
bool operator<(const cow& o) const { return f < o.f; }
};
vector<cow> c[maxn];
int vis[maxn];
int main() {
cin >> n >> m;
inc(i, 1, n) cin >> a[i];
inc(i, 1, m) {
cin >> t >> f;
c[t].push_back({f, n + 1, 0});
}
inc(i, 1, n) sort(c[i].begin(), c[i].end());
inc(i, 1, n) {
int nw = a[i];
pre[nw]++;
if (top[nw] < c[nw].size() && pre[nw] == c[nw][top[nw]].f)
c[nw][top[nw]++].l = i, vis[i] = 1;
}
memset(top, 0, sizeof(top));
memset(pre, 0, sizeof(pre));
dec(i, n, 1) {
int nw = a[i];
pre[nw]++;
if (top[nw] < c[nw].size() && pre[nw] == c[nw][top[nw]].f)
c[nw][top[nw]++].r = i;
}
vis[0] = 1;
inc(lim, 0, n) {
if (!vis[lim]) continue;
ans2[lim] = 1;
inc(i, 1, n) {
if (c[i].size() == 1) {
if (c[i][0].l == lim)
ans1[lim]++;
else {
if (c[i][0].l < lim && c[i][0].r > lim)
ans1[lim]++, ans2[lim] = ans2[lim] * 2 % mod;
else if (c[i][0].l < lim || c[i][0].r > lim)
ans1[lim]++;
}
} else if (c[i].size() > 1) {
int cnt[3] = {0}, fail = 1;
inc(j, 0, c[i].size() - 1) {
if (c[i][j].l == lim)
fail = 0;
else if (c[i][j].l < lim) {
if (c[i][j].r > lim)
cnt[0]++;
else
cnt[1]++;
} else if (c[i][j].r > lim)
cnt[2]++;
}
if (fail) {
if (cnt[0] >= 2 || cnt[0] == 1 && cnt[1] + cnt[2] ||
cnt[1] && cnt[2]) {
ans1[lim] += 2;
ans2[lim] = ans2[lim] *
(cnt[1] * (cnt[0] + cnt[2]) +
cnt[0] * (cnt[0] - 1 + cnt[2])) %
mod;
} else if (cnt[0] + cnt[1] + cnt[2]) {
ans1[lim] += 1;
if (cnt[0])
ans2[lim] = ans2[lim] * 2 % mod;
else
ans2[lim] = ans2[lim] * max(cnt[1], cnt[2]) % mod;
}
} else {
ans1[lim] += 1 + (cnt[0] + cnt[2] > 0);
ans2[lim] = ans2[lim] * max(1, cnt[0] + cnt[2]) % mod;
}
}
}
}
int md = 0;
inc(i, 0, n) md = max(md, ans1[i]);
ll res = 0;
inc(i, 0, n) if (ans1[i] == md) res += ans2[i];
cout << md << " " << res % mod << "\n";
}
1305E - Kuroni and the Score Distribution
题意: 构造一个严格递增的数列 {\(a_i\)}, \(a_i ≤ 1e9\), 使得对于所有三元组 (i, j, k), 1 ≤ i < j < k ≤ n, 满足 \(a_i + a_j = a_k\) 的数量恰为 m.
思路: 考虑对于 {1, 2, ... , n} 这样的一个起始序列, 枚举 k, 会发现有 \(\lfloor \frac{k - 1}{2} \rfloor\) 个满足条件的三元组, 从而得到总的三元组数. 因此 m > \(\sum ^ {n} _ {i=1} {\lfloor \frac{i - 1}{2} \rfloor}\) 可以先判定是不可能有解的. 我们找到这样的 k 使得 $\sum ^ {k} _ {i=1} {\lfloor \frac{i - 1}{2} \rfloor} ≤ m < \sum ^ {k+1} _ {i=1} {\lfloor \frac{i - 1}{2} \rfloor} $ 成立, 而剩下的三元组 res = m - \(\sum ^ {k} _ {i=1} {\lfloor \frac{i - 1}{2} \rfloor}\) 全由 $ a_{k+1} = 2 * k + 1 - res $ (这个数是怎么来的?考虑 $a_{k-2×res+1} + a_k = a_{k+1} $)与前面的数组合搞定. 再后面的数取大奇数防止出现合法三元组就可了, 即它们的间距大于 \(a_{k+1}\) 且 \(a_{k+2}+a_{k+3} > a_n\).
view code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define inc(i, l, r) for (int i = l; i <= r; i++)
const int maxn = 1e6 + 5;
int top, n, m;
int a[maxn];
int main() {
cin >> n >> m;
inc(i, 1, n) a[i] = a[i - 1] + (i - 1) / 2;
int pos = upper_bound(a + 1, a + n + 1, m) - a - 1;
if (a[n] < m) {
cout << "-1\n";
} else {
inc(i, 1, pos) cout << i << " ";
if (pos < n) {
int res = m - a[pos];
cout << 2 * pos + 1 - 2 * res << " ";
inc(i, pos + 2, n) cout << (int)1e6 + 1 + (int)1e4 * (i - pos)
<< " ";
}
cout << "\n";
}
}
1305F - Kuroni and the Punishment
题意: 给出 n 个数 \(a_i\), n ≤ 2e5, \(a_i\) ≤ 1e12. 可以每次使某一个数 +1 / -1 (但要保持还是正数). 问要使这些数的最小公因数不为 1 的最少操作数.
思路: 由于可以对每个数进行至多一次操作, 使得所有数都是偶数, 从而满足题意的要求, 说明答案不大于 n, 进而得知变化次数大于 1 的数的个数不大于 \(\lfloor \frac{n}{2} \rfloor\). 随机取出 \(a_i\) 中的一个数, 设为 x, 至少有 1 / 2 的概率 x 被增减次数是小于等于 1 的, 把 x - 1, x, x + 1 质因数分解, 这样随机取出 20 次后, 最小公因数出现在这些质因数的概率为 \(1-2^{-20}\). 这个集合至多有 $ 60 × \log{a_i} $ 个数. 对于这些可能是最小公因数的质数, 可以每个都 O(n) 地更新答案.
view code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define inc(i, l, r) for (int i = l; i <= r; i++)
const int maxn = 1e6 + 5;
int n;
ll a[maxn], res;
const int maxnum = 1e6;
int prim[maxnum], pvis[maxnum + 5], pcnt;
void getprim() {
for (int i = 2; i <= maxnum; i++) {
if (!pvis[i]) prim[++pcnt] = i;
for (int j = 1; j <= pcnt && prim[j] * i <= maxnum; j++) {
pvis[prim[j] * i] = 1;
if (i % prim[j] == 0) break;
}
}
}
set<ll> s;
int main() {
srand(0);
ios::sync_with_stdio(false);
cin.tie(nullptr);
getprim();
cin >> n;
inc(i, 0, n - 1) cin >> a[i];
res = n;
for (int i = 1, j = rand() % n; i <= 20; i++, j = (j + rand()) % n) {
inc(del, -1, 1) {
ll tmp = a[j] + del;
for (int k = 1; k <= pcnt && tmp > 1; k++) {
if (tmp % prim[k] == 0) {
s.insert(prim[k]);
while (tmp % prim[k] == 0) tmp /= prim[k];
}
}
if (tmp > 1) s.insert(tmp);
}
}
for (ll e : s) {
ll tmp = 0;
inc(i, 0, n - 1) tmp +=
a[i] > e ? min(a[i] % e, e - a[i] % e) : e - a[i];
res = min(tmp, res);
}
cout << res << "\n";
}
题意: 给出一个N(N \(\leq\) 1e5)个点的树, q(q \(\leq\) 1e5)组询问, 每次询问会连接x, y两点, 查询是否存在长度为k的a, b间路径(可以经过重复的边).
思路: 原本树上路径长度是唯一的, 引入x-y后只需考虑在x-y上经过奇数次的情形, 奇数次又可以等效于经过1次. 讨论三种走法, a-b, a-x-y-b, a-y-x-b, 剩下的路程可以模2处理(在一条边上来回走), 而走x-y是唯一可能影响到奇偶性的走法.
view code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define inc(i, l, r) for (int i = l; i <= r; i++)
const int maxn = 1e5 + 5;
const int logn = 20;
int n;
int par[logn][maxn], dep[maxn], root;
vector<int> g[maxn];
void dfs(int v, int p, int d) {
par[0][v] = p;
dep[v] = d;
for (int i = 0; i < g[v].size(); i++)
if (g[v][i] != p) dfs(g[v][i], v, d + 1);
}
void init() {
dfs(root, -1, 0);
for (int k = 0; k + 1 < logn; k++) {
for (int v = 0; v < n; v++) {
if (par[k][v] < 0)
par[k + 1][v] = -1;
else
par[k + 1][v] = par[k][par[k][v]];
}
}
}
int lca(int u, int v) {
if (dep[u] > dep[v]) swap(u, v);
for (int k = 0; k < logn; k++)
if ((dep[v] - dep[u]) >> k & 1) v = par[k][v];
if (u == v) return u;
for (int k = logn - 1; k >= 0; k--) {
if (par[k][u] != par[k][v]) u = par[k][u], v = par[k][v];
}
return par[0][u];
}
int dis(int u, int v) { return dep[u] + dep[v] - 2 * dep[lca(u, v)]; }
int u, v, q, x, y, k;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n;
inc(i, 1, n - 1) {
cin >> u >> v;
u--, v--;
g[u].push_back(v);
g[v].push_back(u);
}
init();
cin >> q;
while (q--) {
cin >> x >> y >> u >> v >> k;
x--, y--, u--, v--;
int d1 = dis(u, v);
int d2 = dis(u, x) + 1 + dis(y, v);
int d3 = dis(u, y) + 1 + dis(x, v);
if (d1 <= k && (k - d1) % 2 == 0 || d2 <= k && (k - d2) % 2 == 0 ||
d3 <= k && (k - d3) % 2 == 0)
cout << "yes\n";
else
cout << "no\n";
}
}
1304F1 - Animal Observation (easy version)
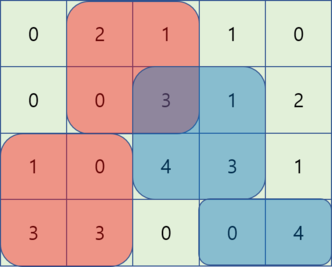
题意: 摄影师要在 n 天拍摄 m 个区域的动物, 每天可以布置一个相机来观察连续 k 个区域, 每次相机可以工作2天(也就是每天会有2个相机在工作, 但是观察区域重叠时不会重复算), 已知每一天每片区域出现的动物数量, 问最多能观察到多少动物. n≤50, m≤2e4, k≤min(m, 20). 下面是从原题盗来的图.
思路: dp[i][j]为在第 i 天布置的相机观察 [j, j + k -1] 区域, 累计最多的观察动物数. 而它会从上一行三种状态转移过来, 即左边不重合, 重合, 右边不重合, 其中不重合就是查询最大的前缀/后缀, 而重合时可以扫描一遍 O(k) 地减去重合部分的影响. 总的时间复杂度为O(nmk).
view code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define inc(i, l, r) for (int i = l; i <= r; i++)
#define dec(i, l, r) for (int i = l; i >= r; i--)
const int maxn = 55;
const int maxm = 2e4 + 5;
int a[maxn][maxm], dp[maxn][maxm], sum[maxn][maxm];
int n, m, k;
int pre[maxn][maxm], suff[maxn][maxm];
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m >> k;
inc(i, 0, n - 1) inc(j, 0, m - 1) cin >> a[i][j];
inc(i, 0, n - 1) inc(j, 0, k - 1) sum[i][0] += a[i][j];
inc(i, 0, n - 1) inc(j, 1, m - k) sum[i][j] =
sum[i][j - 1] + a[i][j + k - 1] - a[i][j - 1];
inc(i, 0, m - k) dp[0][i] = sum[0][i] + sum[1][i];
pre[0][0] = dp[0][0];
inc(i, 1, m - k) pre[0][i] = max(pre[0][i - 1], dp[0][i]);
suff[0][m - k] = dp[0][m - k];
dec(i, m - k - 1, 0) suff[0][i] = max(suff[0][i + 1], dp[0][i]);
inc(i, 1, n - 1) {
inc(j, 0, m - k) {
if (j - k >= 0) dp[i][j] = max(dp[i][j], pre[i - 1][j - k]);
if (j + k <= m - k) dp[i][j] = max(dp[i][j], suff[i - 1][j + k]);
int tmp = 0;
inc(p, j - k + 1, j) {
tmp += a[i][p + k - 1];
if (p >= 0) dp[i][j] = max(dp[i][j], dp[i - 1][p] - tmp);
}
inc(p, j + 1, j + k - 1) {
tmp -= a[i][p - 1];
if (p <= m - k) dp[i][j] = max(dp[i][j], dp[i - 1][p] - tmp);
}
dp[i][j] += sum[i][j] + sum[i + 1][j];
}
pre[i][0] = dp[i][0];
inc(j, 1, m - k) pre[i][j] = max(pre[i][j - 1], dp[i][j]);
suff[i][m - k] = dp[i][m - k];
dec(j, m - k - 1, 0) suff[i][j] = max(suff[i][j + 1], dp[i][j]);
}
cout << pre[n - 1][m - k] << "\n";
}
1304F2 - Animal Observation (hard version)
题意: 与 easy version 唯一的区别在于 k 的取值范围由 k ≤ min(m, 20) 变成 k ≤ m.
思路1: 考虑更快地从上一行得到最大值. 对于 dp[i][j], 我们已经知道了上一行的哪些区域会发生重合并且要减去哪些值, 而对于 dp[i][j + 1], 我们发现每个位置要减去的值仅变化了 a[i][j] 或者 a[i][j + k] 或者不变, 所以可以维护这样的线段树: 当前已处理至 dp[i][j], 线段树中每一个节点代表了上一行的答案减去与 dp[i][j] 重合的部分, 而处理 dp[i][j + 1]前, 上一行范围 [j - k + 1, j] 的节点要 +a[i][j](不再与 a[i][j] 重合), 在范围 [j + 1, j + k] 的节点要 -a[i][j + k] (与 a[i][j + k] 发生重合), 这样就可以在 O(nmlogk)的时间里得到答案了.
解法1
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define inc(i, l, r) for (int i = l; i <= r; i++)
#define dec(i, l, r) for (int i = l; i >= r; i--)
const int maxn = 55;
const int maxm = 2e4 + 5;
int a[maxn][maxm], dp[maxm], nxt[maxm], sum[maxn][maxm];
int n, m, k;
int w[maxm * 4], f[maxm * 4];
void push(int k) {
if (f[k]) {
f[k << 1] += f[k], f[k << 1 | 1] += f[k];
w[k << 1] += f[k], w[k << 1 | 1] += f[k];
f[k] = 0;
}
}
void up(int k) { w[k] = max(w[k << 1], w[k << 1 | 1]); }
void build(int k, int l, int r) {
if (l == r) {
w[k] = dp[l], f[k] = 0;
return;
}
w[k] = f[k] = 0;
int mid = l + r >> 1;
build(k << 1, l, mid);
build(k << 1 | 1, mid + 1, r);
up(k);
}
void change(int k, int l, int r, int val, int a, int b) {
if (a <= l && r <= b) {
w[k] += val, f[k] += val;
return;
}
push(k);
int mid = l + r >> 1;
if (a <= mid) change(k << 1, l, mid, val, a, b);
if (b > mid) change(k << 1 | 1, mid + 1, r, val, a, b);
up(k);
}
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m >> k;
inc(i, 0, n - 1) inc(j, 0, m - 1) cin >> a[i][j];
inc(i, 0, n - 1) inc(j, 0, k - 1) sum[i][0] += a[i][j];
inc(i, 0, n - 1) inc(j, 1, m - k) sum[i][j] =
sum[i][j - 1] + a[i][j + k - 1] - a[i][j - 1];
inc(i, 0, m - k) nxt[i] = sum[0][i] + sum[1][i];
inc(i, 1, n - 1) {
inc(j, 0, m - k) dp[j] = nxt[j], nxt[j] = 0;
int tmp = 0;
dec(j, k - 1, 0) {
tmp += a[i][j];
dp[j] -= tmp;
}
build(1, 0, m - k);
inc(j, 0, m - k) {
nxt[j] = w[1] + sum[i][j] + sum[i + 1][j];
change(1, 0, m - k, a[i][j], max(0, j - k + 1), j);
change(1, 0, m - k, -a[i][j + k], j + 1, min(j + k, m - k));
}
}
int res = 0;
inc(i, 0, m - k) res = max(res, nxt[i]);
cout << res << "\n";
}
思路2: 考虑用单调队列来维护相交部分的最大值, 复杂度可以优化成 O(nm). 对于上下行不相交的情况, 仍然使用前后缀更新; 而相交的部分是这样处理的: 从左往右扫描, 把 dp[i - 1][j] - sum[i][j] 加入队列并保持单调性, 弹出编号为 j - k 的元素, 查询队列最大值, 队列整体 +a[i][j] (因为不再与 a[i][j] 相交, 参见思路 1); 而弹出操作我是给每个元素加了编号, 以编号检查是否要弹出, 查询队列最大值自然是队尾元素, 队列整体增加并没有真正实施, 而是加在了马甲 tmp 上, 查询的时候加上 tmp 即可, 后面压入一个新的数时得减去 tmp 保证比较大小的正确性, 由于压入的数不是原本的真值, 所以我前面要用编号来确定弹出的数还在不在. 个人感觉知道这题是用单调队列和队列整体增加操作后, 后面的细节最好自己解决.
解法2
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define inc(i, l, r) for (int i = l; i <= r; i++)
#define dec(i, l, r) for (int i = l; i >= r; i--)
#define pii pair<int, int>
#define fi first
#define se second
#define pb push_back
const int maxn = 55;
const int maxm = 2e4 + 5;
int a[maxn][maxm], dp[maxm], nxt[maxm], sum[maxn][maxm];
int pre[maxm], suff[maxm];
int n, m, k;
int main() {
ios::sync_with_stdio(false);
cin.tie(nullptr);
cin >> n >> m >> k;
inc(i, 0, n - 1) inc(j, 0, m - 1) cin >> a[i][j];
inc(i, 0, n - 1) inc(j, 0, k - 1) sum[i][0] += a[i][j];
inc(i, 0, n - 1) inc(j, 1, m - k) sum[i][j] =
sum[i][j - 1] + a[i][j + k - 1] - a[i][j - 1];
inc(i, 0, m - k) nxt[i] = sum[0][i] + sum[1][i];
inc(i, 1, n - 1) {
inc(j, 0, m - k) dp[j] = nxt[j], nxt[j] = 0;
pre[0] = dp[0];
inc(i, 1, m - k) pre[i] = max(pre[i - 1], dp[i]);
suff[m - k] = dp[m - k];
dec(i, m - k - 1, 0) suff[i] = max(suff[i + 1], dp[i]);
inc(j, 0, m - k) {
if (j - k >= 0) nxt[j] = max(pre[j - k], nxt[j]);
if (j + k <= m - k) nxt[j] = max(suff[j + k], nxt[j]);
}
int tmp = 0;
deque<pii> que;
inc(j, 0, m - k) {
int now = dp[j] - tmp - sum[i][j];
while (que.size() && que.front().fi < now) que.pop_front();
que.push_front(pii(now, j));
if (j - k >= 0 && que.size() && que.back().se == j - k)
que.pop_back();
nxt[j] = max(nxt[j], que.back().fi + tmp);
tmp += a[i][j];
}
tmp = 0;
que.clear();
dec(j, m - k, 0) {
int now = dp[j] - tmp - sum[i][j];
while (que.size() && que.front().fi < now) que.pop_front();
que.push_front(pii(now, j));
if (j + k <= m - k && que.size() && que.back().se == j + k)
que.pop_back();
nxt[j] = max(nxt[j], que.back().fi + tmp);
tmp += a[i][j + k - 1];
}
inc(j, 0, m - k) nxt[j] += sum[i][j] + sum[i + 1][j];
}
int res = 0;
inc(i, 0, m - k) res = max(res, nxt[i]);
cout << res << "\n";
}
题意: 让一只 cow 在二维矩形方格里不走重复边地尽可能运动.
思路: 模拟, 构造, 见代码. 主要想说写代码前一定要先计算一下自己的走法是不是在数量上等于总的边数, 以及 n, m = 1 等极限情况能否适用.
view code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define inc(i, l, r) for (int i = l; i <= r; i++)
int n, m, k;
struct pii {
int d;
string s;
pii(int d_, string s_) { d = d_, s = s_; }
};
queue<pii> que;
queue<pii> res;
int main() {
cin >> n >> m >> k;
if (k > 4 * n * m - 2 * n - 2 * m) {
cout << "NO\n";
return 0;
}
cout << "YES\n";
if (m == 1) {
if (k <= n - 1)
cout << "1\n" << k << " D\n";
else
cout << "2\n" << n - 1 << " D\n" << k - n + 1 << " U\n";
return 0;
}
inc(i, 1, n - 1) {
if (k) que.push(pii(min(k, m - 1), "R")), k -= min(k, m - 1);
pii tmp = pii(-1, "");
if (k % 3 == 1 && k < 3 * (m - 1)) tmp = pii(1, "D"), k--;
if (k % 3 == 2 && k < 3 * (m - 1)) tmp = pii(1, "DU"), k -= 2;
if (k >= 3)
que.push(pii(min(k / 3, m - 1), "DUL")), k -= min(k / 3, m - 1) * 3;
if (tmp.s.size()) que.push(tmp);
if (k) que.push(pii(1, "D")), k--;
}
if (k) que.push(pii(min(k, m - 1), "R")), k -= min(k, m - 1);
if (k) que.push(pii(min(k, m - 1), "L")), k -= min(k, m - 1);
if (k) que.push(pii(min(k, n - 1), "U")), k -= min(k, n - 1);
cout << que.size() << "\n";
while (que.size())
cout << que.front().d << " " << que.front().s << "\n", que.pop();
}
题意: 给出一个长度为 n 的 01 串和 k 个集合, 集合里面是 1 - n 的一些数, 任意三个集合的交集是空集. 要求选出部分集合, 对于每个集合中的每个数, 都会使得 01 串中的相应位置翻转. 问要使得串前 m 个数都是 1, 最少需要选出的集合数(保证有解). 输出 m 取遍 1 - n 共 n 个答案.
思路: 每个位置最多只会受 2 个集合的选取与否影响. 要使得某一位置的数为 1, 如果该位置受 2 个集合影响, 可以得到这 2 个集合是否会共同存在, 如果受 1 个集合影响, 可以得到这 1 个集合是否会存在. 用带权并查集维护这样的关系, 根节点存储当前块中与根节点共存的数的数量和不共存的(每个节点初始值为 (1, 0)), 对答案的贡献是这两个权值的最小值, 每个节点到根节点的距离的奇偶性反映是否与根节点共存. 同时建立一个特殊的节点, 权值为 (0, inf), 当一个集合被断言存在或不存在时就与该节点相连, 若存在距离为 0; 不存在距离为1.
view code
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define inc(i, l, r) for (int i = l; i <= r; i++)
#define dec(i, l, r) for (int i = l; i >= r; i--)
#define pii pair<int, int>
#define fi first
#define se second
#define pb push_back
const int maxn = 3e5 + 5;
int n, k, q, c;
ll res;
string s;
vector<int> v[maxn];
int par[maxn], dis[maxn];
ll val[maxn][2];
int find(int x) {
if (x == par[x]) return x;
int pp = par[x];
par[x] = find(par[x]);
dis[x] += dis[pp];
return par[x];
}
ll query(int x) {
x = find(x);
return min(val[x][0], val[x][1]);
}
void unite(int x, int y, int d) {
int px = find(x), py = find(y);
if (px != py) {
d = (d + dis[x] + dis[y]) & 1;
res -= query(px), res -= query(py);
par[px] = py;
dis[px] += d;
val[py][0] += val[px][0 ^ d];
val[py][1] += val[px][1 ^ d];
res += query(py);
}
}
int main() {
cin >> n >> k >> s;
inc(i, 1, k) par[i] = i, val[i][0] = 1;
par[k + 1] = k + 1, val[k + 1][1] = (int)1e7;
inc(i, 1, k) {
scanf("%d", &q);
while (q--) {
scanf("%d", &c);
v[c].push_back(i);
}
}
inc(i, 1, n) {
if (s[i - 1] == '1') {
if (v[i].size() == 2) {
unite(v[i][0], v[i][1], 0);
} else if (v[i].size() == 1) {
unite(v[i][0], k + 1, 1);
}
} else {
if (v[i].size() == 2) {
unite(v[i][0], v[i][1], 1);
} else if (v[i].size() == 1) {
unite(v[i][0], k + 1, 0);
}
}
printf("%d\n", res);
}
}

