EM算法

EM算法引入

首先回顾下数据满足单个高斯的场景下我们是如何找到最优参数的，我们是通过极大似然估计，直接求导得到参数结果。

\[\hat{\theta}= \underset{\theta}{argmax}P(X \mid \theta)=\underset{\theta}{argmax}\prod_i^{n}P(x_i \mid \theta) \]

其中 \(\begin{aligned}p(x_i) =\mathcal{N}(x_i \mid \mu, \Sigma) =(2 \pi)^{-k / 2}|\Sigma|^{-\frac{1}{2}} \exp ^{-\frac{1}{2}(x_i-\mu)^{T} \Sigma^{-1}(x_i-\mu)}\end{aligned}\)

为了求解方便，我们一般将其写成：

\[\begin{aligned}\Theta_{\mathrm{MLE}}&=\underset{\Theta}{\arg \max } \mathcal{L}(\Theta \mid X)\\&=\underset{\Theta}{\arg\max}\ log\prod_i^{n}P(x_i \mid \theta)\\&=\underset{\Theta}{\arg\max}\ \sum_i^{n}logP(x_i \mid \theta)\end{aligned} \]

然后求解相应的\(\frac{\partial \mathcal{L}(\Theta \mid X)}{\partial\mu}=0\)和\(\frac{\partial \mathcal{L}(\Theta \mid X)}{\partial\Sigma}=0\)即可。

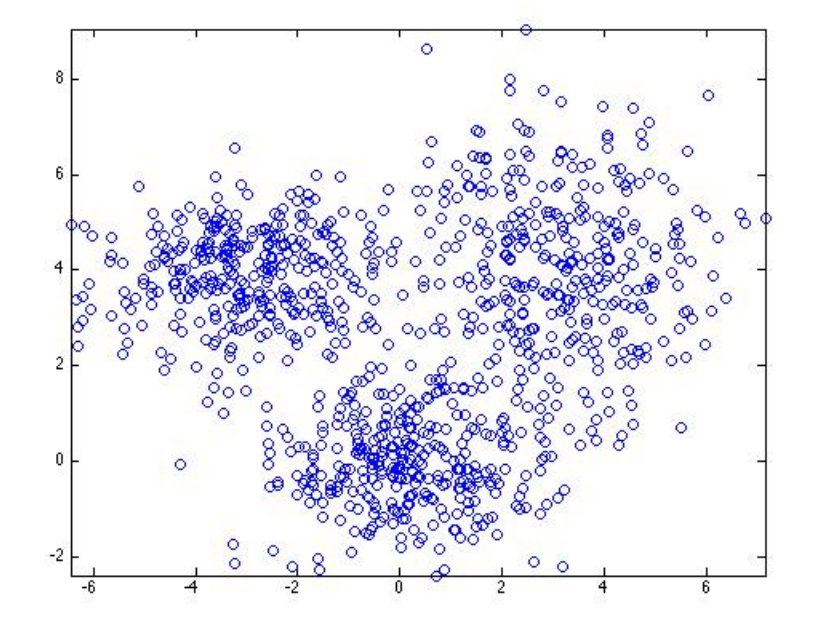
但是现在考虑这样一个数据：

从图中可以看出，大概可以分成三个部分，如果这个数据用一个高斯去拟合的话，显然不会得到很好的结果，那么这个时候我们就需要用多个高斯来拟合。

这个时候的\(P(X)\)就需要写成以下这种形式：

\[P(X)=\sum_{l=1}^{k} \alpha_{l} \mathcal{N}\left(X \mid \mu_{l}, \Sigma_{l}\right) \quad \sum_{l=1}^{k} \alpha_{l}=1 \]

公式的含义是说，当前的概率是由k个高斯分布决定的，每个高斯分布的权重为\(\alpha_l\)，并且要满足权重和为1（为了保证概率满足[0, 1]）。

既然我们已经得到了每个数据的概率，那么就可以带入上面一个高斯的最大似然估计的求解公式中：

\[\begin{aligned} \Theta_{\mathrm{MLE}}&=\underset{\Theta}{\arg \max } \mathcal{L}(\Theta \mid X) \\ &=\underset{\Theta}{\arg\max}\ \sum_i^{n}logP(x_i \mid \theta)\\ &=\underset{\Theta}{\arg \max }\left(\sum_{i=1}^{n} \log \sum_{l=1}^{k} \alpha_{l} \mathcal{N}\left(X \mid \mu_{l}, \Sigma_{l}\right)\right) \end{aligned}\]

那么现在我们的目标就变成了要去求解上面这个式子，这里直接求导令其为就不太容易做到，就需要用到EM算法来帮助我们解出最优结果。

Jensens不等式推导

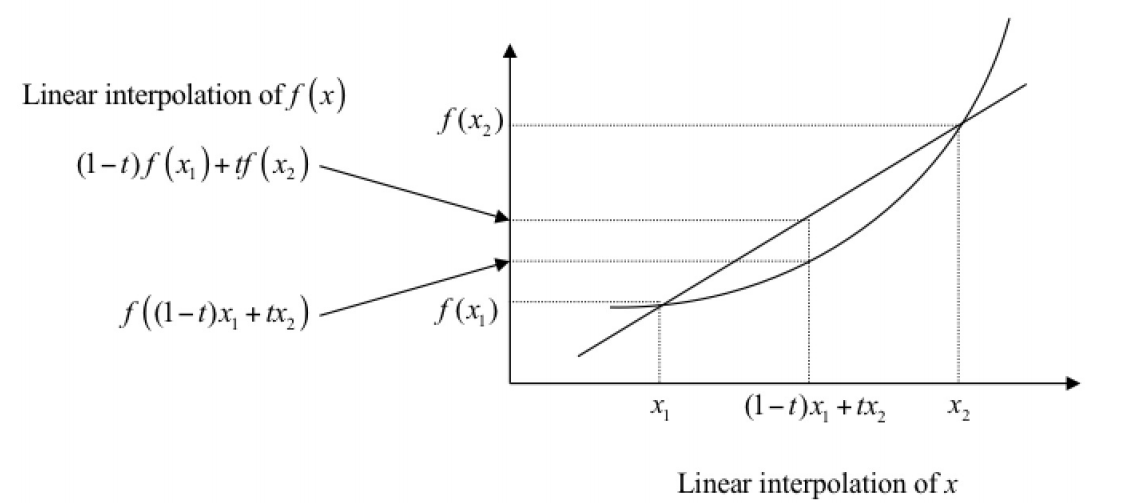
首先我们需要看下凸函数的定义：

其中包含一个小技巧，就是说已知两点A和B，那么两点之间连线的任意一点可以用\((1-t)A+tB\)，其中\(t\in[0, 1]\)。

依据凸函数的图例，我们可以很容易得到以下结论（参考自徐亦达老师的PPT，这里t的取值两个端点应该是可以取到的）：

\[f\left((1-t) x_{1}+t x_{2}\right) \leq(1-t) f\left(x_{1}\right)+t f\left(x_{2}\right) \quad t \in[0 \ldots 1] \]

改写一下上面的式子：

\[\Phi\left((1-t) x_{1}+t x_{2}\right) \leq(1-t) \Phi\left(x_{1}\right)+t \Phi\left(x_{2}\right) \quad t \in[0 \ldots 1] \]

对上面的式子进行一个推广，满足\(\sum_{i=1}^np_i=1\)，式子可以写成：

\[\begin{aligned} &\begin{aligned} \Phi\left(p_{1} x_{1}+p_{2} x_{2}+\ldots p_{n} x_{n}\right) & \leq p_{1} \Phi\left(x_{1}\right)+p_{2} \Phi\left(x_{2}\right) \ldots p_{n} \Phi\left(x_{n}\right) \quad \sum_{i=1}^{n} p_{i}=1 \\ \Longrightarrow & \Phi\left(\sum_{i=1}^{n} p_{i} x_{i}\right) \leq \sum_{i=1}^{n} p_{i} \Phi\left(x_{i}\right) \end{aligned}\\ &\Longrightarrow \Phi\left(\sum_{i=1}^{n} p_{i} f\left(x_{i}\right)\right) \leq \sum_{i=1}^{n} p_{i} \Phi\left(f\left(x_{i}\right)\right) \quad \text { by replacing } x_{i} \text { with } f\left(x_{i}\right) \end{aligned}\]

如果是连续的话，其中：\(\int_{X \in \mathbb{S}} p(x)=1\)，则：

\[\Phi\left(\int_{x \in \mathbb{S}} f(x) p(x)\right) \leq \int_{x \in \mathbb{S}} \Phi\left(f\left(x_{i}\right)\right) p(x) \Longrightarrow \Phi \mathbb{E}[f(x)] \leq \mathbb{E}\left[\Phi\left(f\left(x_{i}\right)\right)\right] \]

最后我们得到一个结论：\(\Phi \mathbb{E}[f(x)] \leq \mathbb{E}\left[\Phi\left(f\left(x_{i}\right)\right)\right]\)。

总结：

1. \(\Phi(x)\)为凸函数，则\(\Phi \mathbb{E}[f(x)] \leq \mathbb{E}\left[\Phi\left(f\left(x_{i}\right)\right)\right]\)。即望函数小于等于函数期望
2. \(\Phi(x)\)为凹函数，则\(\Phi \mathbb{E}[f(x)] \ge \mathbb{E}\left[\Phi\left(f\left(x_{i}\right)\right)\right]\)。即望函数大于等于函数期望

EM公式推导

推导1

首先我们来看，在原来的函数中加入隐变量 \(z\)，该隐变量的分布为 \(g(z)\)：

\[\log p(x \mid \theta)=\log p(z, x \mid \theta)-\log p(z \mid x, \theta)=\log \frac{p(z, x \mid \theta)}{q(z)}-\log \frac{p(z \mid x, \theta)}{q(z)} \]

其中：\(p(x) = \frac{p(z, x)}{p(z\mid x)}\)

对等式两边求期望：

\[\begin{array}{l} \text {Left: } \int_{z} q(z) \log p(x \mid \theta) d z=\log p(x \mid \theta) \\ \text {Right: } \int_{z} q(z) \log \frac{p(z, x \mid \theta)}{q(z)} d z-\int_{z} q(z) \log \frac{p(z \mid x, \theta)}{q(z)} d z=E L B O+K L(q(z), p(z \mid x, \theta)) \end{array} \]

上式中，Evidence Lower Bound(ELBO)，是一个下界，所以 \(\log p(x|\theta)\ge ELBO\)，等于号取在 KL 散度为0是，即：\(q(z)=p(z|x,\theta)\)，EM 算法的目的是将 ELBO 最大化，根据上面的证明过程，在每一步 EM 后，求得了最大的ELBO，并根据这个使 ELBO 最大的参数代入下一步中：

\[\hat{\theta}=\mathop{argmax}{\theta}\ ELBO=\mathop{argmax}\theta\int_zq(z)\log\frac{p(x,z|\theta)}{q(z)}dz \]

由于 \(q(z)=p(z|x,\theta^t)\) 的时候，这一步的最大值才能取等号，所以：

\[\begin{aligned} \hat{\theta}=\underset{\theta}{\arg \max}ELBO &=\mathop{argmax}\theta\int_zq(z)\log\frac{p(x,z|\theta)}{q(z)}dz\\ &=\mathop{argmax}\theta\int_zp(z|x,\theta^t)\log\frac{p(x,z|\theta)}{p(z|x,\theta^t)}d z\ \\ &=\mathop{argmax}_\theta\int_z p(z|x,\theta^t)\log p(x,z|\theta) \end{aligned} \]

这个式子就是EM 迭代过程中的式子。

推导2

从 Jensen 不等式出发，也可以导出这个式子：

\[\log p(x|\theta)=\log\int_zp(x,z|\theta)dz=\log\int_z\frac{p(x,z|\theta)q(z)}{q(z)}dz\ =\log \mathbb{E}{q(z)}[\frac{p(x,z|\theta)}{q(z)}]\ge \mathbb{E}{q(z)}[\log\frac{p(x,z|\theta)}{q(z)}] \]

其中，右边的式子就是 ELBO，等号在 \(p(x,z\mid \theta)= Cq(z)\) 时成立。于是：

\[\int_zq(z)dz=\frac{1}{C}\int_zp(x,z|\theta)dz=\frac{1}{C}p(x|\theta)=1\ \Rightarrow q(z)=\frac{1}{p(x|\theta)}p(x,z|\theta)=p(z|x,\theta) \]

我们发现，这个过程就是上面的最大值取等号的条件。

EM算法的两步：

E step：计算 \(\log p(x,z|\theta)\) 在概率分布 \(p(z|x,\theta^t)\) 下的期望
M step：计算使这个期望最大化的参数得到下一个 EM 步骤的输入

收敛性证明

我们现在已知直接求解多个高斯分布的最大似然函数是不好做的，那么可以通过引入一个隐变量来简化计算，这个隐变量不是随便引入的，必须满足某个条件。

在这里我们引入变量\(z\)，它表示的是当前这个数据属于哪一个高斯分布。

这样子的话，我们可以改写一下优化函数，引入隐变量 \(z\)：

\[\begin{aligned} \mathcal{L}(\theta \mid X) &=\ln [p(X \mid \theta)]=\ln [p(Z, X, \theta)]-\ln [p(Z \mid X, \theta)] \\ &\left(p(Z \mid X)=\frac{p(Z, X)}{p(X)})\Longrightarrow p(X)=\frac{p(Z,X)}{p(Z \mid X)}\right)\end{aligned}\]

然后等式两边同时乘以 \(p\left(z \mid X, \Theta^{(g)}\right)\)，然后对 \(z\) 求积分写成：

\[\begin{aligned} \int_{z \in S} \ln [p(X \mid \theta)] p\left(z \mid X, \Theta^{(g)}\right) \mathrm{d} z &=\int_{z \in S} \ln [p(Z, X, \theta)] p\left(z \mid X, \Theta^{(g)}\right) \mathrm{d} z-\int_{z \in S} \ln [p(Z \mid X, \theta)] p\left(z \mid X, \Theta^{(g)}\right) \mathrm{d} z\end{aligned}\]

其中，观察左边的式子中，可以看到 \(\ln [p(X \mid \theta)]\) 是不包含 \(z\) 的，所以积分内可以提到积分外，后面积分就是关于\(z\)随机变量的，结果等于1，所以：

\[\int_{z \in S} \ln [p(X \mid \theta)] p\left(z \mid X, \Theta^{(g)}\right) \mathrm{d} z=\ln [p(X \mid \theta)]\int_{z \in S} p\left(z \mid X, \Theta^{(g)}\right) \mathrm{d} z=\ln [p(X \mid \theta)] \]

这样子我们上面的式子就化简成：

\[\begin{aligned} \ln [p(X \mid \theta)]&=\underbrace{\int_{z \in S} \ln [p(Z, X, \theta)] p\left(z \mid X, \Theta^{(g)}\right) d z}_{Q\left(\theta, \theta^{(g)}\right)}-\underbrace{\int_{z \in S} \ln [p(Z \mid X, \theta)] p\left(z \mid X, \Theta^{(g)}\right) d z}_{H(\theta, \Theta^{(g)})} \end{aligned}\]

则我们要优化的内容就可以写成：\(Q(\theta, \theta^{(g)})-H(\theta, \Theta^{(g)})\)，这里需要优化两个内容，那么我们是否可以取个巧，只优化一个呢，这样计算不就简单多了，如果只需要优化第一个\(Q(\theta, \theta^{(g)})\)，那不就快乐多多了吗？

下面我们来看下是否可以：

首先明确下我们需要证明的内容：
在E-M算法中，下一步迭代的：\(\Theta^{(g+1)}=\underset{\theta}{\arg \max} Q\left(\theta, \Theta^{(g)}\right)\)
我们需要保证的是每一次迭代过后，它的似然函数是增大的，并且最终能够收敛。

证明：
\(\underset{\theta}{\arg \max }\left[\int_{z \in \mathbb{S}} \ln [p(Z \mid X, \theta)] p\left(z \mid X, \Theta^{(g)}\right) \mathrm{d} z\right]=\Theta^{(g)} \Longrightarrow H\left(\Theta^{(g+1)}, \Theta^{(g)}\right) \leq H\left(\Theta^{(g)}, \Theta^{(g)}\right)\)

\(\mathcal{L}(\Theta^{(g+1)})=\underbrace{Q\left(\Theta^{(g+1)}, \Theta^{(g)}\right)}_{\geq Q(\Theta(g), \Theta(g))}-\underbrace{H\left(\Theta^{(g+1)}, \Theta^{(g)}\right)}_{\leq H(\Theta(g), \Theta(g))} \geq Q\left(\Theta^{(g)}, \Theta^{(g)}\right)-H\left(\Theta^{(g)}, \Theta^{(g)}\right)=\mathcal{L}\left(\Theta^{(g)})\right.\)

这里说明下为什么这样子是可以的，上面证明的式子中：第一个式子的意思是说，当我们最大化\(H(\theta, \Theta^{(g)})\)的时候，得到的结果是\(\Theta^{(g)}\)，那么说明什么，\(H(\Theta^{(g)}, \Theta^{(g)})\)是最大值。注意在优化\(H(\theta, \Theta^{(g)})\)的时候，括号后面的\(\Theta^{(g)}\)是一个常量，不是变量了，我们要得到的结果是\(\theta\)。

那么既然\(H(\Theta^{(g)}, \Theta^{(g)})\)是最大值了，那么必然是大于等于\(H(\Theta^{(g+1)}, \Theta^{(g)})\)的。

第二个式子的话，我们得到了每次优化得到的\(Q\left(\Theta^{(g+1)}, \Theta^{(g)}\right)\)是大于等于\(Q\left(\Theta^{(g)}, \Theta^{(g)}\right)\)，二者相减必然满足大于等于的关系，进而可以得到最终的结论：\(\mathcal{L}(\Theta^{(g+1)})\ge \mathcal{L}(\Theta^{(g)})\)

接下来证明上面的两个式子：

第一个式子的证明：

\[\begin{aligned} \text { 要证明 } & \underset{\theta}{\arg \max }\left[H\left(\theta, \Theta^{(g)}\right)\right]=\underset{\theta}{\arg \max }\left[\int_{z \in \mathbb{S}} \operatorname{In}[p(Z \mid X, \theta)] p\left(z \mid X, \Theta^{(g)}\right) \mathrm{d} z\right]=\Theta^{(g)} \\ \Longrightarrow \text { 也就是以证明 } & H\left(\Theta^{(g)}, \Theta^{(g)}\right)-H\left(\theta, \Theta^{(g)}\right) \geq 0 \quad \forall \theta \end{aligned}\]

证明如下：

\[\begin{aligned} H\left(\Theta^{(g)}, \Theta^{(g)}\right)-H\left(\theta, \Theta^{(g)}\right)&=\int_{z \in \mathbb{S}} \ln \left[p\left(Z \mid X, \Theta^{(g)}\right)\right] p\left(z \mid X, \Theta^{(g)}\right) \mathrm{d} z-\int_{z \in \mathbb{S}} \ln [p(Z \mid X, \theta)] p\left(z \mid X, \Theta^{(g)}\right) \mathrm{d} z \\ &=\int_{z \in \mathbb{S}} \ln \left[\frac{p\left(Z \mid X, \Theta^{(g)}\right)}{p(Z \mid X, \theta)}\right] p\left(z \mid X, \Theta^{(g)}\right) \mathrm{d} z\\ &=\int_{z \in \mathbb{S}}-\ln \left[\frac{p(Z \mid X, \theta)}{p(Z \mid X, \Theta(g))}\right] p\left(z \mid X, \Theta^{(g)}\right) \mathrm{d} z \\ &\geq-\ln \left[\int_{z \in \mathbb{S}} \frac{p(Z \mid X, \theta)}{p\left(Z \mid X, \Theta^{(g)}\right)} p\left(z \mid X, \Theta^{(g)}\right) \mathrm{d} z\right]\\ &=-\ln \left[\int_{z \in \mathbb{S}} p(Z \mid X, \theta)\mathrm{d} z\right]= -\ln(1)=0 \end{aligned}\]

其中大于等于那一步用到了我们上面证明的Jensens不等式，\(-\ln(x)\) 是凸函数，所以是期望函数\(\leq\)函数期望。

第二个式子的证明：

由 \(\Theta\) 的定义：

\[\Theta^{(g+1)}=\underset{\theta}{\arg\max}\ln [p(Z, X, \theta)] p\left(z \mid X, \Theta^{(g)}\right) \]

可以得到\(Q\left(\Theta^{(g+1)}, \Theta^{(g)}\right) \ge Q\left(\theta, \Theta^{(g)}\right)\)。
综上可以得到：\(\mathcal{L}(\Theta^{(g+1)})\ge \mathcal{L}(\Theta^{(g)})\)

参考来自：

1. B站：https://www.bilibili.com/video/BV1aE411o7qd?p=60
2. B站：https://www.bilibili.com/video/BV1Qx411W7mf?p=1
3. 语雀文档：https://www.yuque.com/books/share/f4031f65-70c1-4909-ba01-c47c31398466
4. 语雀文档源文件：https://github.com/tsyw/MachineLearningNotes