组合数学 隔板法

隔板法在排列组合中的应用技巧

张红兵

在排列组合中，对于将不可分辨的球装入到可以分辨的盒子中而求装入方法数的问题，常用隔板法。

例1. 求方程的正整数解的个数。

［分析］

将10个球排成一排，球与球之间形成9个空隙，将两个隔板插入这些空隙中（每空至多插一块隔板），规定由隔板分成的左、中、右三部分的球数分别为x、y、z之值（如下图）。则隔法与解的个数之间建立了一一对立关系，故解的个数为（个）。实际运用隔板法解题时，在确定球数、如何插隔板等问题上形成了一些技巧。下面举例说明。

技巧一：添加球数用隔板法。

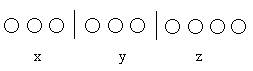
例2. 求方程的非负整数解的个数。

［分析］

注意到x、y、z可以为零，故上题解法中的限定“每空至多插一块隔板”就不成立了，怎么办呢？只要添加三个球，给x、y、z各一个球。这样原问题就转化为求的正整数解的个数了，故解的个数为（个）。

［点评］

本例通过添加球数，将问题转化为如例1中的典型隔板法问题。

 

技巧二：减少球数用隔板法：

例3. 将20个相同的小球放入编号分别为1，2，3，4的四个盒子中，要求每个盒子中的球数不少于它的编号数，求放法总数。

解法1：先在编号1，2，3，4的四个盒子内分别放0，1，2，3个球，剩下14个球，有1种方法；再把剩下的球分成4组，每组至少1个，由例1知方法有（种）。

解法2：第一步先在编号1，2，3，4的四个盒子内分别放1，2，3，4个球，剩下10个球，有1种方法；第二步把剩下的10个相同的球放入编号为1，2，3，4的盒子里，由例2知方法有（种）。

［点评］

两种解法均通过减少球数将问题转化为例1、例2中的典型问题。

关于例一到例二的转化。。

因为x+y+z=3的非负整数解

1,2,0

1,0,2

2,1,0

2,0,1

0,1,2

0,2,1

0,0,3

0,3,0

3,0,0

1,1,1

一共有10种。。

然后我们给每个部分都加一。。

总和是6.。

但是其解得分布全部是正整数。。这就与6个球分成3部分的正整数解

的情况形成了一一对应。。所以我们仍然可以按照例一的情形来理解