从维度理解dp问题
对于dp,我目前的理解就是,干成题目中的那件事需要作出若干次决策,然后你要取其中最优的结果,我们可以用深搜来递归地找最优解,然后我们来观察一下这个递归树的形状,如果它能从底往上直接递推的话,就不用递归了,直接递推迭代到结果。。
当你不知道哪个决策最优时,我的解决方法是,那我们就遍历所有决策,从中选择最优的,当你用深搜遍历所有决策时,题目中的条件或者你自己推的结论可以帮助你进行dfs剪枝
【维度可以是任何东西】
这里先要澄清一个误区。时间和空间本身不是维度,而是“可以用维度概念描述的东西”。空间拥有三个维度,并不是说一维、二维和三维是空间;就像百米赛跑有前三名,但你不能说第一名、第二名和第三名就是百米跑。
维度(dimension)这个概念其实非常基础:允许某种东西自由变化的范围。
-
int dp[n0][n1][n2];
比如上面这个多维数组每个维度n0、n1和n2都可以自由在0到ni-1变化,这正是维度的概念!只不过这些维度是些表面没有太多意义的连续非负整数。
实际上数组下标本身存储了一定的信息,假如他每个维度本身的信息就是一个离散的下标,那么数组下标本身就是我们dp的语义信息
然而除了这种情况,我们可以仅把一个数组下标就当成一个下标,他真正的意义(的值)储存在A[index]中,或者其他更复杂的数据结构
例如树上的一条链,一个凸包,或者是一个边集,点集,向量集,矩阵,线段树的某一子树,某值的集合等等等等,每个维度的下标变换可以
链接到外面的资源
在后面声明的一点是。。当我们分析出了这个dp问题的状态图之后,我们要保证dp的顺序正确,即在这个DAG中要按照拓扑序去考虑递推的顺序,
什么是拓扑序呢,我们可以参考拓扑排序的定义以及拓扑序的定义。
二、状态
事物具有多个维度,反之多个维度就能共同描述一个事物,而多个维度的值就描述了事物的状态。
比如说,导航程序,经度和纬度这两个维度的值就能描述当前某用户的状态,即这个用户正在某经度某维度的地方。
对应于数组,经度、纬度两个维度对应了二维数组:
-
int dp[MaxLng][MaxLat];
如果多维数组各个维度的值确定后,那么就相当于确定了在多维数组中具体哪一个单元格。因此可以这么说,各个单元格就对应了各个状态,数组就是状态的集合,而状态就是通过确定数组各个维度的值定位的!
-
dp[x][y]所对应的单元格就表示人在经度x纬度y的状态
不过,单元格可不仅仅是单元格,因为数组可以是bool类型、int类型等等,即这个单元格有值的。这个值就是状态的值,而状态该是什么类型的值,取值是多少这取决于具体的问题。
注意,上面说到值有两个,红色字,一个是维度的值,一个是状态的值,其中维度的值描述了具体的状态。
比如说,上面的导航程序的数组是int类型,这样dp[x][y]就可以拿来表示人在到达经度x纬度y这个状态所需的时间(分钟数)。
再比如说,如果数组是bool类型,这样dp[x][y]就可以拿来表示人能否到达经度x纬度y这个状态。
在动态规划问题里,状态的值经常是最小值、最大值和方案数等。一般就是从已知的初始状态的值,通过状态的转移,得出最终目标状态的值。
不过,上面提到的这个“状态”还不是动态规划里的“状态”,因为还少了一样东西——请看下一节,【无后效性】。
三、无后效性
动态规划的状态必须是无后效性的。下面我用一道题目具体说明什么是无后效性。
有一楼梯共M级,刚开始时你在第一级,若每次只能跨上一级或二级,要走上第M级,共有多少种走法?
这个问题里面很容易找到一个维度:楼梯的级数。那么到达第i级台阶就是一个状态,简称状态i,问题所需要求的是到达状态i的方案数,即:
- dp[i]表示到达第i级台阶的方案数
i的取值是从1到M,也就是说有M个状态。这M个状态之间是有关系的。比如可以从第1级的台阶直接移动到第2级或者第3级,或者第5级台阶可以从第3级或者第4级台阶直接移动到。
下面就M取5画一张状态图:

这张图上面的顶点表示的是各个状态,有向边(弧)就表示状态的转移。事实上这张图是一张有向无环图(DAG, Directed Acyclic Graph),即从任何一点出发不可能回到自身。
也就是说在那张图中状态i是通过状态i-1和状态i-2确定的,并且和状态i-3、i-4、i-5...没有一点关系,之后状态i也不会影响到状态i-3、i-4、i-5…,i-3、i-4、i-5状态的值已经是确定好的。
这就是无后效性。动态规划的状态必须是无后效性的状态。
动态规划本质上可以理解成在一个DAG上的递推:入度0的状态点就是初始的状态,有向边说明了状态转移的方向,通过状态的转移按着DAG的拓扑序推出最终目标状态的值。而由于是DAG,状态不会重复经过,最多就经过所有的状态。
具体如何转移请看下一节,【状态转移】。
四、状态转移
前面提到了,动态规划的过程就是从初始状态转移到最终的目标状态,而初始状态的值是知道的,目标状态的值就是问题需要的。
还是那一题【超级楼梯】,状态(的值)是这么表示的:
-
dp[i]表示到达第i级台阶的方案数
而转移的表示,通常当然不是画图,而是写出状态转移方程:
- dp[i] = 1 (i=1)
- dp[i] = dp[i-1] (i=2)
- dp[i] = dp[i-1] + dp[i-2] (i>2)
为什么是这样呢?可以从之前画的状态图中理解。
- 首先dp[1]就表示到达台阶1的方案数,一开始就在台阶1,这个状态的值当然就是1了,即dp[1]=1,而事实上这个也正是初始状态;
- 然后dp[i]=dp[i-1](i=2),也就是说dp[2]=dp[1],因为走到台阶2只有一种策略就会从台阶1走来,因而到达台阶2的方案数就等于达到台阶1的方案数,也就是1;
- 最后dp[i]=dp[i-1]+dp[i-2](i>2),这个从语义上理解是这样的:走到i-1的方案数是dp[i-1],然后向上走一步就到了i,因而状态i的方案数就有dp[i-1];而走到i-2的方案数是dp[i-2],然后向上走2步就到了i,因而状态i的方案数又可以有dp[i-2]种;总共就是dp[i-1]+dp[i-2]个方案数。
那么有了状态转移方程,就可以动手写程序实现了。具体程序的实现多种多样,但要注意的是状态的值一定要按拓扑序依次求出。下面我讲讲讲三种方式:“人人为我”、“我为人人”和记忆化搜索。其中“人人为我”和“我为人人”这两个是我从北大ACM-ICPC暑期课的课件中学到的。
- “人人为我”
这个很常见,就是上面转移方程表示的那样。
状态图大概可以这么看:
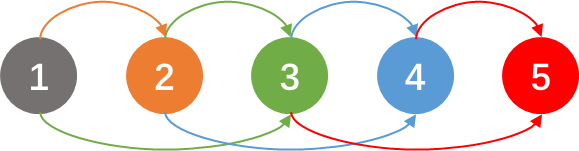
比如可以看到状态5就是从3和4转移过来的。
写成程序就是这样:
- #include<cstdio>
- usingnamespace std;
- int dp[41];
- int main(){
- dp[1]=1; dp[2]=1;
- for(int i=3; i<=40;++i){
- dp[i]=dp[i-1]+dp[i-2];
- }
- int N,M;
- scanf("%d",&N);
- while(N--){
- scanf("%d",&M);
- printf("%d\n",dp[M]);
- }
- return0;
- }
- “我为人人”
这个是从当前状态顺着推过去,更新能到达状态的值。
这个实现起来挺直观的,因为是顺着往前推。
状态图可以这么看:

比如可以看到状态1更新到2和3。
写成程序是这样的:
- #include<cstdio>
- usingnamespace std;
- int dp[44];
- int main(){
- dp[1]=1;
- for(int i=1; i<40;++i){
- dp[i+1]+=dp[i];
- dp[i+2]+=dp[i];
- }
- int N,M;
- scanf("%d",&N);
- while(N--){
- scanf("%d",&M);
- printf("%d\n",dp[M]);
- }
- return0;
- }
- 记忆化搜索
一般都是用DFS实现,就是用搜索当前状态能从哪儿转移过来。
另外开一个数组记录搜索过的状态的值,避免重复搜索,时间复杂度就不会是指数级的了,而是多项式级。
有时候用记忆化搜索很直观,而且记忆化搜索还可以避免搜索无意义、不需要的状态,从而使效率提升。
这个直接上代码吧:
- #include<cstdio>
- usingnamespace std;
- int dp[44];
- int dfs(int i){
- if(dp[i]!=0)return dp[i];
- return dp[i]=dfs(i-1)+dfs(i-2);
- }
- int main(){
- dp[1]=1; dp[2]=1;
- int N,M;
- scanf("%d",&N);
- while(N--){
- scanf("%d",&M);
- printf("%d\n",dfs(M));
- }
- return0;
- }
二、状态
事物具有多个维度,反之多个维度就能共同描述一个事物,而多个维度的值就描述了事物的状态。
比如说,导航程序,经度和纬度这两个维度的值就能描述当前某用户的状态,即这个用户正在某经度某维度的地方。
对应于数组,经度、纬度两个维度对应了二维数组:
-
int dp[MaxLng][MaxLat];
如果多维数组各个维度的值确定后,那么就相当于确定了在多维数组中具体哪一个单元格。因此可以这么说,各个单元格就对应了各个状态,数组就是状态的集合,而状态就是通过确定数组各个维度的值定位的!
-
dp[x][y]所对应的单元格就表示人在经度x纬度y的状态
不过,单元格可不仅仅是单元格,因为数组可以是bool类型、int类型等等,即这个单元格有值的。这个值就是状态的值,而状态该是什么类型的值,取值是多少这取决于具体的问题。
注意,上面说到值有两个,红色字,一个是维度的值,一个是状态的值,其中维度的值描述了具体的状态。
比如说,上面的导航程序的数组是int类型,这样dp[x][y]就可以拿来表示人在到达经度x纬度y这个状态所需的时间(分钟数)。
再比如说,如果数组是bool类型,这样dp[x][y]就可以拿来表示人能否到达经度x纬度y这个状态。
在动态规划问题里,状态的值经常是最小值、最大值和方案数等。一般就是从已知的初始状态的值,通过状态的转移,得出最终目标状态的值。
不过,上面提到的这个“状态”还不是动态规划里的“状态”,因为还少了一样东西——请看下一节,【无后效性】。




