尾调用与尾递归

本讲将对尾调用与尾递归进行介绍：函数的最后一条执行语句是调用一个函数的形式即为尾调用；函数尾调用自身则为尾递归，通过改写循环即可轻松写出尾递归函数。在语言支持尾调用优化的条件下，尾调用能节省很大一部分内存空间。

什么是尾调用

问：何为尾调用？
说人话：函数的最后一条执行语句是调用一个函数，这种形式就称为尾调用。

让我们看看以下几个例子。

// 正确的尾调用：函数/方法的最后一行是去调用function2()这个函数
public int function1(){
    return function2();
}

// 错误例子1：调用完函数/方法后，又多了赋值操作
public int function1(){
    int x = function2();
    return x;
}

// 错误例子2：调用完函数后，又多了运算操作
public int function1(){
    return function2() + 1;
}

// 错误例子3：f(x)的最后一个动作其实是return null
public void function1(){
    function2();
}

尾调用优化

以Java为例。JVM会为每个新创建的线程都创建一个栈（stack）。栈是用来存储栈帧（stack frame）的容器；而栈帧是用来保存线程状态的容器，其主要包括方法的局部变量表（local variable table），操作数栈（operand stack），动态连接（dynamic linking）和方法返回地址（return address）等信息。
（注：Java语言目前还不支持尾调用优化，但尾调用优化的原理是相通的。）

栈会对栈帧进行压栈和出栈操作：每当一个Java方法被执行时都会新创建一个栈帧（压栈，push），方法调用结束后即被销毁（出栈，pop）。

在方法A的内部调用方法B，就会在A的栈帧上叠加一个B的栈帧。在一个活动的线程中，只有在栈顶的栈帧才是有效的，它被称为当前栈帧（Current Stack Frame），这个栈帧所关联的方法则被称为当前方法（Current Method）。只有当方法B运行结束，将结果返回到A后，B的栈帧才会出栈。

举个例子。

public int eat(){
    return 5;
}

public int action(){
    int x = eat();
    return x;
}

public int imitate(){
    int x = action();
    return x;
}

public static void main(String[] args){
    imitate();
}

这段代码对应的栈的状况则为如下：

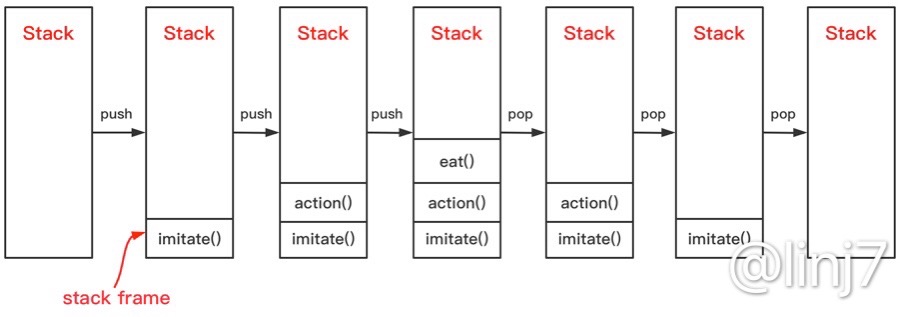
首先，在main线程调用了imitate()方法，便将它的栈帧压入栈中。
在imitate()方法里，调用了action()方法，由于这不是个尾调用，在调用完action()方法后仍存在一个运算操作，因此将\(action\)的栈帧压入栈中后，JVM认为imitate()方法还没执行完，便仍然保留着\(imitate\)的栈帧。
同理：action()方法里对eat()方法的调用也不是尾调用，JVM认为在调用完eat()方法后，action()方法仍未执行结束。因此保留\(action\)的栈帧，并继续往栈中压入\(eat\)的栈帧。
eat()方法执行完后，其对应栈帧就会出栈；action()方法和imitate()方法在执行完后其对应的栈帧也依次出栈。

但假如我们对上述示例代码改写成如下所示：

public int eat(){
    return 5;
}

public int action(){
    return eat();
}

public int imitate(){
    return action();
}

public static void main(String[] args){
    imitate();
}

那么如果尾调用优化生效，栈对应的状态就会为如下：

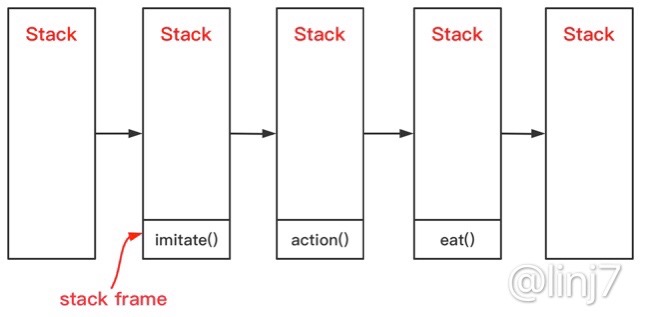
首先，仍然是将imitate()方法的栈帧压入栈中。
在imitate()方法中对action()方法进行了尾调用，因此在调用action()方法时就意味着imitate()方法执行结束：\(imitate\)栈帧出栈，\(action\)栈帧入栈。
同理：\(action\)栈帧出栈，\(eat\)栈帧入栈。
最后，eat()方法执行完毕，全流程结束。

我们可以看到，由于尾调用是函数的最后一条执行语句，无需再保留外层函数的栈帧来存储它的局部变量以及调用前地址等信息，所以栈从始至终就只保留着一个栈帧。这就是尾调用优化(tail call optimization)，节省了很大一部分的内存空间。

但上面只是理论上的理想情况，把代码改写成尾调用的形式只是一个前提条件，栈是否真的如我们所愿从始至终只保留着一个栈桢还得取决于语言是否支持。例如python就不支持，即使写成了尾递归的形式，栈该爆还是会爆。

尾递归

问：何为尾递归？
说人话：函数尾调用自身，这个形式就称为尾递归。

在手把手教你写递归这篇文章中我们提过，递归对空间的消耗大，例如计算factorial(1000)，就需要保存1000个栈帧，很容易就导致栈溢出。

但假如我们将其改为尾递归，那对于那些支持尾调用优化的语言来说，就能做到只保存1个栈帧，有效避免了栈溢出。

那尾递归函数要怎么写呢？

一个比较实用的方法就是先写出用循环实现的版本，再把循环中用到的局部变量都改为函数的参数即可。这样再进入下一层函数时就不需要再用到上一层函数的环境了，到最后一层时就包含了前面所有层的计算结果，就不要再返回了。

例如阶乘函数。

public int fac(int n) {
    int result = 1;
    for (int index = 1; index <= n; index++)
        result = index * result;
    return result;
}

在这个用循环实现的版本中，可以看到用到了\(result, index\)这两个局部变量，那就将其改为函数的参数。并且通过循环可以看出边界条件是当index == n时；\(n\)从头到尾不会变；\(index\)在每次进入下一层循环时会递增，\(result\)在每次进入下一层循环时会有变动。我们把这些改动直接照搬，改写就非常容易了。

所以用尾递归实现的版本即为如下：

public int fac(int n, int index, int result) {
    if (index == n)
        return index * result;
    else 
        return fac(n, index + 1, index * result);
}

再举个例子，斐波那契数列（0, 1, 1, 2, 3, 5, 8, 13...）

其循环实现版本如下：

public int fibo(int n) {
    int a = 0;
    int b = 1;
    int x = 0;
    for (int index = 0; index < n; index++){
    	x = b;
        b = a + b;
        a = x;
    }
    return a;
}

局部变量有\(a, b, index\)（\(x\)作为\(a, b\)赋值的中间变量，在递归中可以不需要用到），把这些局部变量放到参数列表。边界条件为当index == n时；并且，在进入下一层循环时，\(a\)的值会变为\(b\)，\(b\)的值会变为\(a + b\)，\(index\)的值加1，把这些改动照搬。

public int fibo(int n, int a, int b, int index) {
    if (index == n) 
        return a;
    else 
        return fibo(n, b, a + b, index + 1);
}

参考

创作不易，点个赞再走叭～

posted @ 2020-12-20 13:04 说人话阅读(753) 评论(0) 编辑收藏举报

刷新页面返回顶部

说人话

说点大家都听得懂的话。

尾调用与尾递归

什么是尾调用

尾调用优化

尾递归

参考