Debug心得&笔记「持续更新」
① scanf读取单个字符「2021/8/6」
scanf 的 %c 读取的是单个字符,是连续的!
如:scanf("%c%c",&ch1,&ch2),输入 ab 则接受 ab,但若输入 a b 则会接收 a 。
解决方案:scanf("%c %c",&ch1,&ch2),注意只是加了个空格。
② switch语句的参数类型「2021/8/6」
switch 语句的参数类型只能为 int、char 等,不能为实型「浮点数、实数等」或字符串!!!
③ 输入字符串(string)「2021/8/6」
scanf("%s %s",book[i].name,temptype);
运行时报错:
[Error] cannot pass objects of non-trivially-copyable type 'std::string {aka class std::basic_string<char>}' through '...'
[Error] cannot pass objects of non-trivially-copyable type 'std::string {aka class std::basic_string<char>}' through '...'
分析:
这里的 book[i].name 和 temptype 均为 string 类型。
语法:
const char c_str();c_str()函数返回一个指向正规 C 字符串的指针, 内容与string相同。- 为了与C兼容,在C中没有
string类型,故必须通过string类对象的成员函数c_str()把string对象转换成 C 中的字符串样式。
解决方案:
在要打印的string后面加.c_str()即可。
更正后:
scanf("%s %s",book[i].name.c_str(),temptype.c_str());
然而,上面的分析都是错的!!!
虽然修改后编译可以通过,但运行结果仍然是错的——输入后根本没有为book[i].name和temptype赋值!
解决方案的解决方案:
cin>>book[i].name>>temptype;
总结:
输入字符串,千万不要用 scanf!!!
用 cin!!!
④ 字符串(string)赋值「2021/8/6」
string sort1[k+1]={0},sort2[k+1]={0};
运行时报错「编译已通过」:
terminate called after throwing an instance of 'std::logic_error'
what(): basic_string::_M_construct null not valid
Aborted (core dumped)
分析:
我竟然给字符串赋值为 0 ……
解决方案:
直接赋为空集:
string sort1[k+1]={},sort2[k+1]={};
⑤ C++ 精度修正问题「2021/8/7」
原题:求解一元二次方程
原代码:
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
double a,b,c,x1,x2,delta;
int main()
{
cin>>a>>b>>c;
delta=b*b-4*a*c;
if(delta<0)cout<<"No answer!";
else if(delta>0) printf("x1=%.5lf;x2=%.5lf",min((-b-sqrt(delta))/(2*a),(-b+sqrt(delta))/(2*a)),max((-b-sqrt(delta))/(2*a),(-b+sqrt(delta))/(2*a)));
else printf("x1=x2=%.5lf",(-b)/(2*a));//x1+x2=-b/a,x1=x2时,x1=x2=-b/2a
return 0;
}
测试信息:一个测试点 WA 了。
分析:
C/C++ 中,浮点数的运算(和函数)有可能存在误差。
例如,在经过大量计算后,由于误差的影响,整数 \(1\) 变成了 \(0.9999999999\)。
因此,浮点数只有完全一样才能使用 == 判断相等。
解决方案:
可以借助修正写法,fabs(a–b)<eps,可以自定义精度 esp,esp 一般取 1e-8 左右大小。
比如double类型的 \(a\) 和 \(b\),要判断\(a=b\),在一定的精度范围内比较大小。
修正后:
#include<iostream>
#include<cstdio>
#include<cmath>
#define eps1 1e-10//定义精度esp 10的-10次方
#define eps2 1e-6//定义精度esp 10的-6次方
using namespace std;
double a,b,c,x1,x2,delta;
int main()
{
cin>>a>>b>>c;
delta=b*b-4*a*c;
if(delta<0&&abs(delta)>eps1)cout<<"No answer!";//(修正写法)
else if(abs(delta)<eps1)printf("x1=x2=%.5lf",(-b)/(2*a));//x1+x2=-b/a,x1=x2时,x1=x2=-b/2a //(修正写法)
else
{
x1=(-b+sqrt(delta))/(2*a);
x2=(-b-sqrt(delta))/(2*a);
printf("x1=%.5lf;x2=%.5lf",min((-b-sqrt(delta))/(2*a),(-b+sqrt(delta))/(2*a)),max((-b-sqrt(delta))/(2*a),(-b+sqrt(delta))/(2*a)));
}
return 0;
}
⑥ C++ 中的对数函数「2021/8/9」
知识点:
-
exp(x):求\(e^x\) -
log2(x):返回\(\log_2x\) -
log10(x):返回\(\log_{10}x\)
注意:
C++没有自定义的对数函数!!!
就是说,无法提供 loga(b)——\(\log_ab\)!!!
但是,可以通过换底公式间接地来求。
代码如下:
#include<iostream>
#include<cmath>
using namespace std;
int main()
{
double a,b;//以a为底数,b为真数的对数函数
cin>>a>>b;
cout<<"loga(b)="<<log(b)/log(a)<<endl;//换底公式
return 0;
}
换底公式:
\(\forall a,c\in(0,1)\cup(1,+\infty)\)且\(b\in(0,+\infty)\),有:
证明:
若有 \(a^x=b\) ,则
又因为
因此
代回①式,得:
证毕。
⑦ floor、ceil 取整问题「2021/8/19」
用 floor、ceil 取整时,得到的返回值是浮点数!!!
这就导致一些题不明不白就 WA 了……
解决方案: 强制类型转换,前面加个 (int) 或 (long long)。
⑧ ! 右结合性问题「2021/8/20」
! 右结合性非常强,用的时候一定不要忘了加括号!!!
运行结果错误:
while(!x%(int)pow(2,t)){t++;}
显然,这里的 ! 与 x 结合到了一起,x 是非 \(0\) 的数,!x 就变成了\(0\),这不是我们想要的结果。
更正:
while(!(x%(int)pow(2,t))){t++;}
⑨ 数组&数据类型问题「2021/8/29」
数组不是基础数据类型,而是构造数据类型。
【基础数据类型有 bool、char、int、float、double、void、wchar_t「宽字符型」】
注:
宽字符型wchar_t是这样来的:
typedef short int wchar_t;
所以 wchar_t 实际上的空间和 short int 一样
关于wchar_t,详见这篇博客。
一些基本类型可以使用一个或多个类型修饰符进行修饰,如 signed、unsigned、short和 long。
关于typedef:
可以使用其为一个已有的类型取一个新的名字。
\(e.g.\)
typedef long long ll;
ll a; //声明变量
其实这就相当于:
#define ll long long
ll a;
两者看上去很相似,但区别还是很大的,详见这篇文章和这篇文章。
回到正题。
正因为数组不是基础数据类型,所以在 stack 和 queue 中,像这样用就会报错:
#include<iostream>
#include<typeinfo>
#include<cxxabi.h>
#include<stack>
#include<queue>
using namespace std;
template<typename type>
inline string type_of(type &x)
{
return abi::__cxa_demangle(typeid(x).name(),0,0,0);
}
stack<char[200]>a;
queue<char[200]>b;
signed main()
{
cout<<type_of(a)<<endl;
cout<<type_of(b)<<endl;
return 0;
}

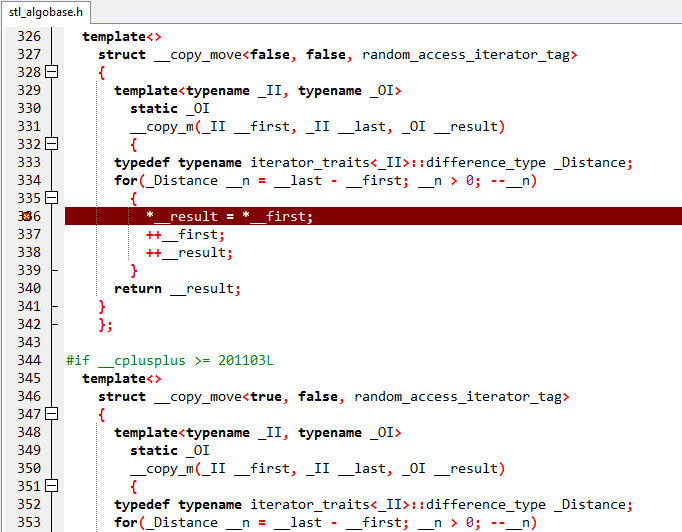
改成string就好了:
#include<iostream>
#include<typeinfo>
#include<cxxabi.h>
#include<stack>
#include<queue>
using namespace std;
template<typename type>
inline string type_of(type &x)
{
return abi::__cxa_demangle(typeid(x).name(),0,0,0);
}
stack<string>a;
queue<string>b;
signed main()
{
cout<<type_of(a)<<endl;
cout<<type_of(b)<<endl;
return 0;
}
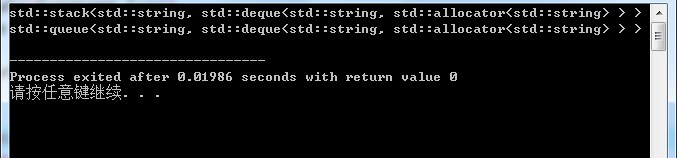
不过玄学的是,用在 vector 好像可以过编译???
#include<iostream>
#include<typeinfo>
#include<cxxabi.h>
#include<vector>
using namespace std;
template<typename type>
inline string type_of(type &x)
{
return abi::__cxa_demangle(typeid(x).name(),0,0,0);
}
vector<char[200]>n;
signed main()
{
cout<<type_of(n)<<endl;
return 0;
}
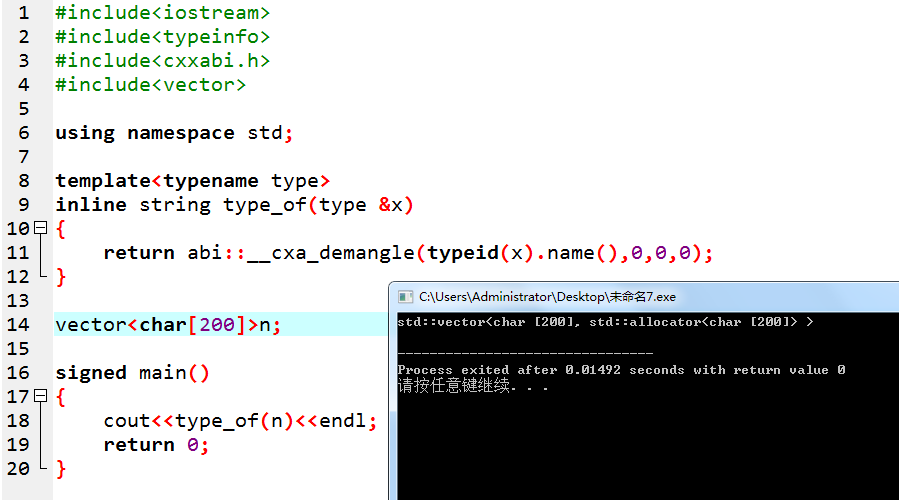
但如下,在用 \(n\) 数组的时候又会报错:
如果改为vector<string>n就不会报错了,但这又是为什么?
求高手指教~
⑩ 关于 static「2021/9/1」
听一个学长说,static 放快写里可以卡常(虽然他也不明白怎么回事)。
然后我一听来精神了,一并将其写进了快读里……
第一天啥事没有,题目照常 AC。
但在第二天:
我竟然被一个单调队列的黄题卡了一上午……
我百思不得其解,最后调了好久代码,才发现竟然是快读出问题了。。。
template<typename type>
inline void read(type &x)
{
x=0;static bool flag(0);char ch=getchar();
while(!isdigit(ch)) flag^=ch=='-',ch=getchar();
while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
flag?x=-x:0;
}
第4行的 flag 是用来判断输入负号的,我顺手将其用 static 修饰,幻想它能卡一点常数,结果显然:
(听取 WA 声一片……)
这个快读读取正数是没有错误的,读取一个负数也可以,但读完一个负数继续正数就错了,后面的符号全变负:
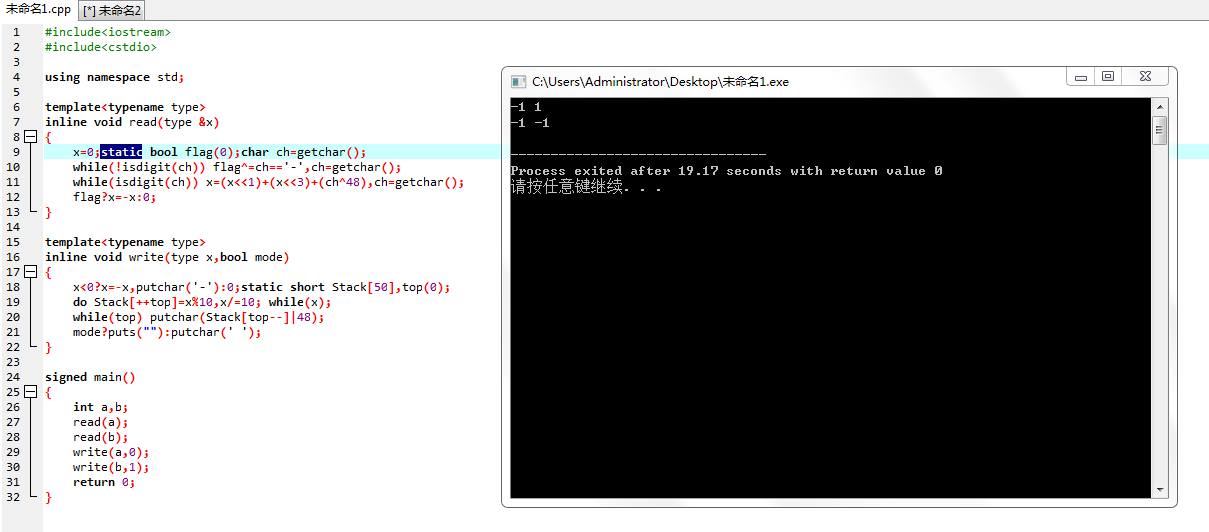
简单查了下 static 的用法,很快就找到了答案:
修饰局部变量时,表明该变量的值不会因为函数终止而丢失
显然,若读进的第一个数为负,则 flag 就变为 \(1\)。
快读结束时,flag 由于 static 的作用,不会像普通变量一样退出函数就被销毁。
因此再读第二个数时,已经存在的 flag 就不会被新的声明影响,仍保持 \(1\) 的值,所以同样会读成负数。。。
解决方案:
将 static 去掉就可以啦。
那么对于快写:
template<typename type>
inline void write(type x,bool mode)
{
x<0?x=-x,putchar('-'):0;static short Stack[50],top(0);
do Stack[++top]=x%10,x/=10; while(x);
while(top) putchar(Stack[top--]|48);
mode?puts(""):putchar(' ');
}
为什么这里用 static 就没事呢?
很简单,因为对于每次快写的调用,都能保证栈空「top 为 \(0\)」,重复声明、赋值与否,都不会对结果造成影响。
这时,用 static 关键字就可以跳过无用的多次声明、赋值阶段,从而节省运行时间。
总结:
对于很多陌生的关键字,
不要乱用!
不要乱用!!
不要乱用!!!
⑪ 码风导致的 RE「2022/7/21」
好久没在洛谷做题了,随便交了一发,\(\color{purple}RE\)!。。
折腾好久才发现,竟然是码风问题。
原来的模板:
#include<iostream>
#include<cstdio>
using namespace std;
signed solve()
{
//codes...
}
signed _=solve();
signed main(){return 0;}
出于未知原因\(\color{purple}{RE}\)。
修改后\(\color{green}{AC}\):
#include<iostream>
#include<cstdio>
using namespace std;
signed main()
{
//codes...
return 0;
}
求指教~
⑫ 爆 int「2022/9/19」
「已经犯了 \(\infty\) 次这种错误才想起来总结一下……」
即使用 long long 类型的变量储存运算结果,也要注意参与运算的变量是否会发生整数溢出!
若参与运算的变量全为 int 类型,记得在前面乘一个 1ll!
⑬ 重载运算符「2022/9/29」
直到今天才弄清重载运算符两种写法的区别:
bool operator <(node a,node b):不会出错,但很慢,原因是调用时会拷贝两个 node 结构体中所有的成员变量,比如若结构体中有很大的数组,则拷贝的时间开销会很大。
bool operator <(const node &a,const node &b):直接用 & 取地址进行操作,避免拷贝的时间开销,同时用 const 避免原结构体内容被修改。
综上,若无需修改结构体内容,推荐用第二种方式重载运算符。
同时,括号中的参数在无 const 时,函数只能接受非 const 参数,传入 const 参数就会报错。而加上 const 后,函数就能同时接受 const 和非 const 参数,扩大了接受参数的范围。「常量不可修改,但能参与运算。」
若括号外面加 const,如下:
bool operator <(const node &a,const node &b)const{
//do something...
}
其作用是使函数可以被 const 对象调用。如:
const node operator +(const node &x)const{
//do something...
}
const node a=(1,2);
node b=(3,4),c=a+b;
不加 const node operator +(const node &x)const 的最后一个 const 会报错。
原因很简单,a 是常量、b 是变量,由于重载了 +,上面最后一行代码中 c=a+b 等同于 a.operator+(b)「由常量 a 调用的 operator+ 函数」,因此调用该函数的是个常量。正因如此,该函数末尾的 const 是不可或缺的。「之前写的高精度板子中,int operator [](int i)const{return a[i];} 不加 const 就会报错。」
⑭ 各类运算符的效率比较「2022/10/4」
| 运算符 | 单位时间开销 |
|---|---|
&&、` |
|
&、` |
、^`、`<<`、`>>` |
<、>、<=、>=、==、!= |
\(32\) |
+、- |
\(64\) |
* |
\(1024\) |
/、% |
\(>10^5\) |
综上:
- 尽量把除法转化为乘法「如
if (a<b/c)换为if(a*c<b)」 *2、/2用<<1、>>1代替「分治、倍增、状压」x*10用(x<<1)+(x<<3)代替「快读」- 若 \(x<n\) ,则
x=(x+1)%n用x=(++x^n?x:0)代替「循环队列」
⑮ 负数取模、随机数「2022/10/12」
今天对拍时发现了bug,生成负的随机数出了问题,经过测试才发现了一个神器的性质:
c++ 的取模运算中,被除数与余数符号相同。
即:若 \(a\%b=c\),则 \(a、c\) 同号,\(c\) 的符号与 \(b\) 无关。
因此,一个随机数 \(\%p(p>0)\) 的结果不一定在 \([0,p-1]\) 中,而是在 \([1-p,p-1]\) 中。
设 \(x\) 为一个随机数,则 \(x\%p+p-1\) 的结果在 \([0,2p-2]\) 中。
\(x\%p+p-1+L\) 的结果在 \([L,2p-2+L]\) 中。
因此,要获得 \([L,R]\)「\(L,R\) 可能为负」中的随机数,有:\(2p-2+L=R\),解出:\(p=\frac{R-L}2+1\)。
由此可以写出一个在 \([L,R]\) 区间内生成随机数的函数:
template<typename type>
inline type R(type L,type R)
{
type t=((R-L)>>1)+1;
return 1ll*rand()*rand()*rand()%t+t-1+L;
}
甚至,还可以更简洁一点:
auto R=[](const auto &L,const auto &R)->auto{auto t=((R-L)>>1)+1;return 1ll*rand()*rand()*rand()%t+t-1+L;};
调用:
signed main()
{
int n,m;
read(n),read(m);
write(R(n,m));
return 0;
}
⑯ unordered_map 与 map「2022/10/16」
昨天打比赛,T1 竟然因为开了 map 挂了 20 分,改为 unordered_map 就能 AC。
因此要提醒自己:
unordered_map 的查找、插入、删除操作平均时间复杂度均为 \(O(1)\),而 map 上述操作的平均时间复杂度均为 \(O(\log n)\)!!!
二者的具体区别:
unordered_map |
map |
|
|---|---|---|
| 查找 | 平均:\(O(1)\qquad\)最坏:\(O(n)\) | \(O(\log n)\) |
| 插入 | 平均:\(O(1)\qquad\)最坏:\(O(n)\) | \(O(\log n)+\)平衡二叉树所用时间 |
| 删除 | 平均:\(O(1)\qquad\)最坏:\(O(n)\) | \(O(\log n)+\)平衡二叉树所用时间 |
| 是否排序 | 不排序 | 排序 |
| 实现方法 | 哈希表 | 红黑树 |
unordered_map 查询单个 key 的时候效率比 map 高,但是要查询某一范围内的 key 值时比 map 效率低。
⑰ 不同命名空间的宏定义冲突「2022/10/22」
#include<iostream>
#include<cstdio>
using namespace std;
namespace A
{
#define maxn 100
signed main()
{
printf("%d\n",maxn);
return 0;
}
#undef maxn
}
namespace B
{
#define maxn 200
signed main()
{
printf("%d\n",maxn);
return 0;
}
#undef maxn
}
signed main()
{
A::main();
B::main();
return 0;
}
运行结果:
100
200
显然未发生宏定义冲突。
若稍作修改,将 namespace A 中的 #undef maxn 去掉,运行结果同上,但编译器会发出警告:
1.cpp:18:13: warning: 'maxn' macro redefined [-Wmacro-redefined]
#define maxn 200
^
1.cpp:7:13: note: previous definition is here
#define maxn 100
^
1 warning generated.
可以看到,maxn 在 namespace B 中相当于又被定义了一遍,覆盖了上次的定义。
因此,我们可以料到:
#include<iostream>
#include<cstdio>
using namespace std;
#define maxn 300
namespace A
{
#define maxn 100
signed main()
{
printf("%d\n",maxn);
return 0;
}
}
namespace B
{
#define maxn 200
signed main()
{
printf("%d\n",maxn);
return 0;
}
}
int a[maxn];
signed main()
{
A::main();
B::main();
printf("%d\n",maxn);
return 0;
}
输出结果为:
100
200
200
a 数组的大小被设为 200 而不是 300,这不是我们想要的结果。我们希望各个命名空间的宏定义互不影响。
于是想到是否可以这样:「即在每个命名空间中,用完 maxn 的结果就取消其在该命名空间的宏定义」
#include<iostream>
#include<cstdio>
using namespace std;
#define maxn 300
namespace A
{
#define maxn 100
signed main()
{
printf("%d\n",maxn);
return 0;
}
#undef maxn
}
namespace B
{
#define maxn 200
signed main()
{
printf("%d\n",maxn);
return 0;
}
#undef maxn
}
int a[maxn];
signed main()
{
A::main();
B::main();
printf("%d\n",maxn);
return 0;
}
这次编译器不干了,直接报错:
1.cpp:34:19: error: use of undeclared identifier 'maxn'; did you mean 'main'?
printf("%d\n",maxn);
^~~~
main
1.cpp:30:8: note: 'main' declared here
signed main()
^
呵呵,看来我们取消 namespace B 中 maxn 的定义,影响到最外面的 maxn 了。
那怎么办呢?
在 C++11 中添加了一个新的关键字 constexpr,这个关键字是用来修饰常量表达式的。
「所谓常量表达式,指的就是由多个『\(\ge1\) 个』常量(值不会改变)组成,并且在编译过程中就得到计算结果的表达式。」
值不会改变,并且在编译过程就能得到计算结果,这恰好可以满足我们的要求。
注意:声明为 constexpr 的常量一定是一个 const 常量,而且必须用常量表达式初始化。例如:
constexpr int a=1;
constexpr int b=a+1;
constexpr int c=f();
constexpr int d;
-
第一行中,
1是常量表达式,正确。 -
第二行中,
a+1是常量表达式,正确。 -
第三行中,当且仅当
f是一个constexpr函数时才是一条正确的声明语句。 -
第四行中,未对
d进行初始化,错误。会报错:error: default initialization of an object of const type 'const int'。
到此为此,我们可以将先前的错误代码进行更改:
#include<iostream>
#include<cstdio>
using namespace std;
constexpr int maxn=300;
namespace A
{
#define maxn 100
signed main()
{
printf("%d\n",maxn);
return 0;
}
#undef maxn
}
namespace B
{
#define maxn 200
signed main()
{
printf("%d\n",maxn);
return 0;
}
#undef maxn
}
int a[maxn];
signed main()
{
A::main();
B::main();
printf("%d\n",maxn);
return 0;
}
输出结果:
100
200
300
a 数组的大小成功设置为 300。
同时,如果你像我一样比较懒,可以将 constexpr int maxn=300 写为 constexpr auto maxn=300。
甚至可以这样:
#include<iostream>
#include<cstdio>
using namespace std;
constexpr auto maxn=300;
constexpr auto PI=3.14;
constexpr auto x=2147483648;
signed main()
{
printf("%d\n",maxn);
printf("%lf\n",PI);
printf("%ld\n",x);
return 0;
}
输出:
300
3.140000
2147483648
但是,如果你这么用:
#include<iostream>
#include<cstdio>
#include<cmath>
using namespace std;
constexpr auto PI=acos(-1);
signed main()
{
printf("%lf\n",PI);
return 0;
}
是会报错的:
1.cpp:5:16: error: constexpr variable 'PI' must be initialized by a constant expression
constexpr auto PI=acos(-1);
^ ~~~~~~~~
1.cpp:5:19: note: non-constexpr function 'acos<int>' cannot be used in a constant expression
constexpr auto PI=acos(-1);
^
因为 acos 返回的不是常量。想将其在编译阶段强制转化为常量或许可以,「不知道用 c++17 刚加的 as_const 行不行」但肯定比较麻烦,所以还是乖乖地用 #define PI acos(-1) 或 const auto PI=acos(-1) 吧。
关于 constexpr 的更多高级用法,可以参考这篇博客。
⑱ nth_element 的使用方式「2022/10/27」
已知 \(a\) 数组中有 \(a_1\)~\(a_n\) 共 \(n\) 个元素,要求在 \(O(n)\) 时间内求出其第 \(k\) 小元素,可以使用头文件 <algorithm> 中的 nth_element 函数。
用法:
nth_element(first,nth,last) 或 nth_element(first,nth,last,comp)。
其中,first、nth、last 都是随机访问迭代器。「这意味着,nth_element() 函数只适用于 array、vector、deque 这 3 个容器。」该函数的作用范围为 [first,last),功能是查找第 nth 大的元素,并将其移动到 nth 指向的位置 \(a_{\text{nth}}\)。
注意使用 nth_element 后并不保证 \(a_k\) 前面和后面部分各自有序,只是 \(a_k\) 位置存放第 \(k\) 小。
错误示范:
nth_element(a+1,a+k+1,a+n+1);
cout<<a[k]<<endl;
正确代码:
nth_element(a+1,a+k,a+n+1);
cout<<a[k]<<endl;
不要把 nth 和 last 的作用范围弄混了!last 指向 \(a_{\text{last}+1}\),但 nth 指向 \(a_{\text{nth}}\)!
然后就导致比赛时痛失 \(5pts\)……
⑲ #define 版 min、max 的一个错误 & 各类 min、max 效率比较「2022/11/4」
强烈建议先看看这篇文章:【C++中#define宏定义的min与max函数】。这篇文章十分详细地讲解了使用 #define 定义的 min、max 和 <algorithm> 头文件中 std::min、std::max 的区别。下面先对重点进行简要概括。
-
#define定义的min、max-
实现
#define max(a,b) ((a)<(b)?(b):(a)) #define min(a,b) ((a)<(b)?(a):(b))直接用三目运算符实现,简洁明了。
-
问题
这样做看似没有问题。之前这种写法我用了大概半年多的时间,一直没有出现问题。
对于比较简单的操作,例如取两个简单变量的最大值、最小值:
#include<iostream> #include<cstdio> #define max(a,b) ((a)<(b)?(b):(a)) #define min(a,b) ((a)<(b)?(a):(b)) signed main() { int a=1,b=2; printf("%d %d",min(a,b),max(a,b)); return 0; }这样完全没有问题,输出:
1 2。但是,如果这样用:
#include<iostream> #include<cstdio> #define max(a,b) ((a)<(b)?(b):(a)) #define min(a,b) ((a)<(b)?(a):(b)) signed main() { int a=1,b=2; printf("%d %d",min(++a,++b),max(a,b)); return 0; }由于先执行
++a、++b,因此 \(a=2\)、\(b=3\),我们期望的输出为2 3。但是实际输出的是
3 3。 -
分析
这是因为,
define只是做简单的文本替换,printf("%d %d",min(++a,++b),max(a,b));展开后为:printf("%d %d",((++a)<(++b)?(++a):(++b)),((a)<(b)?(b):(a)));可以看到,
++a实际被执行了两次:一次在判断(++a)<(++b)时执行,另一次在返回结果时执行。因此,在宏定义的参数中,最好不要出现多次运算会改变结果的表达式,否则很容易出错。
类似地,如果一个函数作为上面
min或max的参数,那么该函数同样会被调用两次,分别在判断和返回结果时执行。因此,若该函数内部较复杂、运算效率较低或在内部也调用
min或max,那么其效率之低可想而知。这也是上面那篇文章的博主写【普通平衡树】时因为宏定义的min和max而超时的原因。其在文中也提到了,可以先用一个变量保存函数结果,再对该变量使用min或max。当然,用 STL<algorithm>头文件中的min、max函数就没有这样的问题。 -
解决
在调用
min前执行++a、++b即可。#include<iostream> #include<cstdio> #define max(a,b) ((a)<(b)?(b):(a)) #define min(a,b) ((a)<(b)?(a):(b)) signed main() { int a=1,b=2; ++a,++b; printf("%d %d",min(a,b),max(a,b)); return 0; }
-
-
各类
min、max效率比较-
各种实现方法
-
上面讲过的
#define#define max(a,b) ((a)<(b)?(b):(a)) #define min(a,b) ((a)<(b)?(a):(b)) -
auto+ lambda 表达式auto max=[](const auto &x,const auto &y)->auto{return x<y?y:x;}; auto min=[](const auto &x,const auto &y)->auto{return x<y?x:y;}; -
STL
std::max、std::min。其内部实现如下:template<class T> inline const T& max(const T& a,const T& b){ return a<b?b:a; } template<class T,class Compare> inline const T& max(const T& a,const T& b,Compare comp){ return comp(a,b)?b:a; } template<class T> inline const T& min(const T& a,const T& b){ return b<a?b:a; } template<class T,class Compare> inline const T& min(const T& a,const T& b,Compare comp){ return comp(b,a)?b:a; }其中
Compare comp是自定义比较函数。 -
template函数模板「其实和 STL 大致相同,但听 hzh 说 STL 有编译器优化。是不是真的不知道,但好像 STL 的确快一些?」
template<typename type> inline type max(const type &x,const type &y){return x<y?y:x;} template<typename type> inline type min(const type &x,const type &y){return x<y?x:y;}
-
-
效率对比
我将上面各种实现方法放到不同的命名空间,实现相同的操作「\(10^8\) 次操作」,多次运行代码进行对比:
#include<iostream> #include<cstdio> using namespace std; namespace test_define { #define max(a,b) ((a)<(b)?(b):(a)) #define min(a,b) ((a)<(b)?(a):(b)) signed main() { int a=2,b=2,c; for(int i=1;i<=100000000;++i) ++a,++b,c=max(a,b),--b,--c,a=min(b,c); printf("%d %d %d\n",a,b,c); return 0; } #undef max #undef min } namespace test_auto { auto max=[](const auto &x,const auto &y)->auto{return x<y?y:x;}; auto min=[](const auto &x,const auto &y)->auto{return x<y?x:y;}; signed main() { int a=2,b=2,c; for(int i=1;i<=100000000;++i) c=max(++a,++b),a=min(--b,--c); printf("%d %d %d\n",a,b,c); return 0; } } namespace test_STL { signed main() { int a=2,b=2,c; for(int i=1;i<=100000000;++i) c=std::max(++a,++b),a=std::min(--b,--c); printf("%d %d %d\n",a,b,c); return 0; } } namespace test_function { template<typename type> inline type max(const type &x,const type &y){return x<y?y:x;} template<typename type> inline type min(const type &x,const type &y){return x<y?x:y;} signed main() { int a=2,b=2,c; for(int i=1;i<=100000000;++i) c=max(++a,++b),a=min(--b,--c); printf("%d %d %d\n",a,b,c); return 0; } } namespace test_STL_rewrite { template<class T> inline const T& max(const T& a,const T& b){ return a<b?b:a; } template<class T> inline const T& min(const T& a,const T& b){ return b<a?b:a; } signed main() { int a=2,b=2,c; for(int i=1;i<=100000000;++i) c=max(++a,++b),a=min(--b,--c); printf("%d %d %d\n",a,b,c); return 0; } } signed main() { //test_define::main(); //test_auto::main(); //test_STL::main(); //test_function::main(); //test_STL_rewrite::main(); return 0; }实现 #defineautoSTL 函数模板 重写 STL 用时 0.48s 0.83s 0.65s 0.80s 0.40s 由于测试具有随机性,我将各种实现方法用在 【洛谷P3865 【模板】ST 表】中进行测试。
该题模板如下:
#include<iostream> #include<cstdio> #include<cmath> #define maxn 1000010 using namespace std; int n,q,l,r; template<typename type> inline void read(type &x) { x=0;bool flag(0);char ch=getchar(); while(!isdigit(ch)) flag^=ch=='-',ch=getchar(); while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar(); flag?x=-x:0; } template<typename type> inline void write(type x,bool flag=1) { x<0?x=-x,putchar('-'):0;static short Stack[50],top(0); do Stack[++top]=x%10,x/=10;while(x); while(top) putchar(Stack[top--]|48); flag?putchar('\n'):putchar(' '); } class st { public: void init() { for(int i=1;i<=n;++i) read(f[i][0]); for(int i=1;i<=n;++i) Log[i]=log(i)/log(2); for(int j=1;j<=Log[n]+1;++j) for(int i=1;i+(1<<(j-1))<=n;++i) f[i][j]=max(f[i][j-1],f[i+(1<<(j-1))][j-1]); } int query(int l,int r) { int k=Log[r-l+1]; return max(f[l][k],f[r-(1<<k)+1][k]); } private: int f[maxn][30],Log[maxn]; }s; signed main() { read(n),read(q); s.init(); while(q--) read(l),read(r),write(s.query(l,r)); return 0; }测试结果如下:「每项进行五次测试取平均值」「为了测试,开了洛谷3个小号QaQ……」
实现 #defineautoSTL 函数模板 重写 STL 用时「不开 O2优化」 911.6ms 934.0ms 941.2ms 934.2ms 915.6ms 用时「开 O2优化」 921.4ms 923.4ms 926.2ms 926.4ms 978.1ms #define和重写 STL 实现的好像厌氧?「很有可能是因为评测机波动……」为了再次减少测试的随机性,我再次将各种实现方法用在 【洛谷P5146 最大差值】这道更加适合用来测试
min、max性能的题中进行测试。「然后再次开了3个小号……洛谷不要怪我qwq……」测试代码:
#include<iostream> #include<cstdio> #include<climits> #define ll long long using namespace std; ll n,x,tmax=-1e10,tmin=1e10; template<typename type> inline type read(type &x) { x=0;bool flag(0);char ch=getchar(); while(!isdigit(ch)) flag^=ch=='-',ch=getchar(); while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar(); return flag?x=-x:x; } template<typename type> inline void write(type x,bool flag=1) { x<0?x=-x,putchar('-'):0;static short Stack[50],top(0); do Stack[++top]=x%10,x/=10;while(x); while(top) putchar(Stack[top--]|48); flag?putchar('\n'):putchar(' '); } signed main() { read(n); for(int i=1;i<=n;++i) read(x),tmax=max(tmax,x-tmin),tmin=min(tmin,x); write(tmax); return 0; }同样每项进行五次测试取平均值,结果如下:
实现 #defineautoSTL 函数模板 重写 STL 用时「不开 O2优化」 152.8ms 154.5ms 156.6ms 153.2ms 157.2ms 用时「开 O2优化」 105.6ms 106.0ms 108.2ms 106.4ms 105.2ms 此次试验结果差距不明显,于是用一组加强数据「\(n=10^8\),\(a_i\) 在
long long范围内」重新测试。数据生成:「Linux,终端」
(echo 100000000 && for ((i=1;i<=100000000;++i));do echo $RANDOM$RANDOM$RANDOM;done)>data.in测试代码:
#include<iostream> #include<cstdio> #include<climits> #define ll long long using namespace std; ll n,x,tmax=-1e15,tmin=1e15; template<typename type> inline type read(type &x) { x=0;bool flag(0);char ch=getchar(); while(!isdigit(ch)) flag^=ch=='-',ch=getchar(); while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar(); return flag?x=-x:x; } template<typename type> inline void write(type x,bool flag=1) { x<0?x=-x,putchar('-'):0;static short Stack[50],top(0); do Stack[++top]=x%10,x/=10;while(x); while(top) putchar(Stack[top--]|48); flag?putchar('\n'):putchar(' '); } signed main() { read(n); for(int i=1;i<=n;++i) read(x),tmax=max(tmax,x-tmin),tmin=min(tmin,x); write(tmax); return 0; }测试结果:
实现 #defineautoSTL 函数模板 重写 STL 用时「不开 O2优化」 30.78s 30.88s 31.23s 30.92s 32.53s 用时「开 O2优化」 25.37s 25.15s 25.53s 25.12s 25.18s 可以看到,即使在数据较大的情况下,几种不同的实现方法在效率上也没有较大差别。
关于某某实现方法能优化常数之类的说法,或许是真的,但优化前后区别不大。因此,选用哪种实现方法,看个人喜好即可。
-
⑳ i++ 和 ++i 的那些事儿「2022/11/8」
关于 i++ 和 ++i,能说的有很多。去年接触其关于常数的争论、重载运算符问题,再到今年刚听说的左值、右值问题,都十分有趣。这里一一展开介绍。
共性
i++ 和 ++i 的作用都是使变量自增加 \(1\)。
单独使用时,二者效果相同,都是 i=i+1。
区别
作为右值时二者有区别。「准确来说是亡值。后面【值类别】中会讲右值和亡值是什么,这里可以先感性理解为等号右边的值。」
a=i++等价于t=i,a=t,i=i+1。a=++i等价于i=i+1,a=i。
即使描述得不是十分准确,也能看出:
i++是先赋值、再自增,++i是先自增、再赋值。i++用到了中间变量,而++i没有。i++不能作为左值,而++i可以。「左值在后面也会介绍,同样可以先感性理解为等号左边的值。」
原理
在这里,研究原理最好的方式是看汇编代码。
先来看单独使用的情形:
int main()
{
int i=0;
i++;
++i;
return 0;
}
利用在线工具 Compiler Explorer「可以在线查看编译后代码块对应的汇编语句,支持选择不同的编译器」生成的对应汇编代码如下:「ARM64 gcc 9.3」
main:
sub sp, sp, #16
str wzr, [sp, 12]
ldr w0, [sp, 12]
add w0, w0, 1
str w0, [sp, 12]
ldr w0, [sp, 12]
add w0, w0, 1
str w0, [sp, 12]
mov w0, 0
add sp, sp, 16
ret
可以看到,无论是 i++ 还是 ++i,在单独使用时,汇编代码完全相同:
ldr w0, [sp, 12]
add w0, w0, 1
str w0, [sp, 12]
汇编指令这里不多作介绍,大体理解即可:
-
ldr和mov类似,其作用可以理解把源操作数送给目的操作数。「感性理解为“赋值”。」在 ARM 架构下,数据从内存到 CPU 之间的移动只能通过 LDR/STR 指令来完成。而 MOV 只能在寄存器之间移动数据,或者把立即数移动到寄存器中,并且数据的长度不能超过 \(8\) 位。
LDR、STR 的第一操作数是目标寄存器,第二操作数是内存地址:
LDR:内存->寄存器
STR:寄存器->内存 -
add是不带进位的加法指令,这里add w0, w0, 1即为w0=w0+1。
可以发现在简单使用时,二者的效率相同。
先前有观点认为 ++i 的效率比 i++ 高,事实上在编译器优化后完全相同。
下面来看一下作为右值的情形:
int main()
{
int i=0,a,b;
a=i++;
b=++i;
return 0;
}
汇编代码如下:
main:
sub sp, sp, #16
str wzr, [sp, 12]
ldr w0, [sp, 12]
add w1, w0, 1
str w1, [sp, 12]
str w0, [sp, 8]
ldr w0, [sp, 12]
add w0, w0, 1
str w0, [sp, 12]
ldr w0, [sp, 12]
str w0, [sp, 4]
mov w0, 0
add sp, sp, 16
ret
分开来看二者的汇编代码:
-
a=i++ldr w0, [sp, 12] add w1, w0, 1 str w1, [sp, 12] str w0, [sp, 8] -
b=++ildr w0, [sp, 12] add w0, w0, 1 str w0, [sp, 12] ldr w0, [sp, 12] str w0, [sp, 4]
通过汇编代码,可以很清楚地看到二者的不同:
a=i++:先将i赋值给a,再进行了+1操作,把+1结果赋值给i。b=++i:先进行+1操作,再将+1结果赋值给i,最后赋值给b。
这里也很清楚地可以看出 a=i++ 用到了两个寄存器 w0 和 w1,而 b=++i 只用了一个寄存器 w0。
练习
既然看了这么多,做几道题检验一下你是否听懂了没。(狗头
求下面 i 的值。
-
int i=0;i=++i;解析
答案显然是 1。
开始时 i=0,++i 先对 i 进行 +1 操作,此时 i 的值为 1。
等号右边的值为 1,将其赋值给左边的 i,最后 i 的值为 1。 -
int i=0;i=i++;解析
这个问题很经典,答案也不那么显然。
你可能认为最终 i 的值为 1,因为有 i++ 操作。实际上 i 的值最后为 0。
开始时 i=0,i++ 先保存结果——0,然后对 i 进行 +1 操作,此时 i 的值为 1。
注意,重点来了:等号右边的值为 0,将其赋值给左边的 i,最后 i 的值为 0。
因此,最后的结果并没有受到等号右边 i++ 使 i 自增的影响,只用到了等号右边整体的值。
可以理解为 = 的优先级低于 ++,先计算 ++ 的结果,再进行赋值。 -
int i=0;i=++i+i+++i+++ ++i;解析
题外话:如果写成 i=++i+i+++i+++++i 会过不了编译,必须加上空格。
看起来稍微难了一点,但理解了第二种情况也很好计算。
同样,因为受运算符优先级影响,我们只需要算出等号右边的值,这就是最终 i 的值。
我们可以把右边的式子拆成这四项:++i、i++、i++、++i,答案即为它们返回值的和。
开始时 i=0,++i 使 i 自增变为 1,返回值为 1,因此第一项的值为 1。
此时 i=1,i++ 返回值为 1,因此第二项的值为 1,然后 i 自增变为 2。
此时 i=2,i++ 返回值为 2,因此第二项的值为 2,然后 i 自增变为 3。
此时 i=3,++i 使 i 自增变为 4,返回值为 4,因此第四项的值为 4。
注意最终 i 的值只与等号右边的整体结果有关,因此答案为这四项返回值的和:1+1+2+4=8。最终 i=8。
重载运算符
在我们自定义结构体/类时,相信大家都会重载运算符,比如:
#include<iostream>
#include<cstdio>
using namespace std;
class node
{
public:
int x,y;
};
node operator +(node a,node b)
{
return {a.x+b.x,a.y+b.y};
}
int main()
{
node A={1,1},B={2,2},C;
C=A+B;
cout<<C.x<<' '<<C.y;
return 0;
}
运行结果为 3 3。
那么如何重载 ++ 和 -- 运算符呢?
以 ++ 为例,你应该能很轻松写出如下代码:「以 ++ 为例,-- 同理。」
#include<iostream>
#include<cstdio>
using namespace std;
class node
{
public:
int x;
};
node operator ++(node &a)
{
return {++a.x};
}
int main()
{
node A={1};
++A;
cout<<A.x;
return 0;
}
输出:2。
但是这样就有一个问题:如何区分前置 ++ 和 -- 两种情况?
其实只需要在后面多加一个参数区分一下就可以啦:
node operator ++(node &a,int)
{
return {a.x++};
}
完整代码:
#include<iostream>
#include<cstdio>
using namespace std;
class node
{
public:
int x;
};
node operator ++(node &a)
{
return {++a.x};
}
node operator ++(node &a,int)
{
return {a.x++};
}
node operator --(node &a)
{
return {--a.x};
}
node operator --(node &a,int)
{
return {a.x--};
}
int main()
{
node A={1};
++A,A++,--A,A--;
return 0;
}
也可以将重载运算符作为类的成员函数,看起来更简洁一些,个人习惯这样写:
#include<iostream>
#include<cstdio>
using namespace std;
class node
{
public:
int x;
node operator ++(){return {++x};}
node operator ++(int){return {x++};}
node operator --(){return {--x};}
node operator --(int){return {x--};}
};
int main()
{
node A={1};
++A,A++,--A,A--;
return 0;
}
同时,++、-- 的重载运算符也支持模板,直接在 class node 和每个重载运算符前面用 template<typename type> 且所有参数类型改为 type 即可。
效率
再回到效率问题的讨论。
前面已经说过,简单使用时 i++ 和 ++i 效率相同。
但是,在重载了运算符的自定义类中,情况就不尽相同了!
下面两段内容引自参考资料,本人进行了一些修改和总结:
由于要生成临时对象,
i++需要调用两次拷贝构造函数与析构函数「将原对象赋给临时对象一次,临时对象以值传递方式返回一次」。
++i由于不用生成临时变量,且以引用方式返回,故没有构造与析构的开销,效率更高。所以在使用类等自定义类型的时候,应尽量使用
++i。
如果只是对变量自增,没有使用
i++或++i的值,那么二者的汇编代码相同,效率也相同。而如果使用了自增或自减之后表达式的值,那么汇编代码就不同了。不过因为int是内置类型,所以即使是这样也并不会使效率有明显差距。但如果是 STL 中的迭代器进行自增、自减操作,那么效率差距就比较大了。因为 STL 并不内建于编译器,只是标准库中的普通 C++ 代码,所以编译器不能对其进行优化。因此,STL 迭代器尽量不要使用后置自增自减。
值类别
这部分内容主要引自【OI Wiki——值类别】,感兴趣的可以直接阅读原文。下面仅摘录与本文相关的内容。
注意:这部分的内容很可能对算法竞赛无用,但如果你希望更深入地理解 C++,写出更高效的代码,那么本文的内容也许会对你有所帮助。
C 和 C++11 以前
C 语言沿用了相似的分类方法,但左右值的判断标准已经与赋值运算符无关。在新的定义中,lvalue 意为 locate value,即能进行取地址运算 (
&) 的值。可以这么理解:左值是有内存地址的对象,而右值只是一个中间计算结果(虽然编译器往往需要在内存中分配地址来储存这个值,但这个内存地址是无法被程序员感知的,所以可以认为它不存在)。中间计算结果就意味着这个值马上就没用了,以后不会再访问它。
比如在
int a = 0;这段代码中,a就是一个左值,而0是一个右值。「常见的关于左右值的误解:」
以下几种类型是经常被误认为右值的左值:
- 字符串字面量:由于 C++ 兼容 C 风格的字符串,需要能对一个字符串字面量取地址(即头指针)来传参。但是其他的字面量,包括自定义字面量,都是右值。
- 数组:数组名就是数组首个元素的指针这种说法似乎误导了很多人,但这个说法显然是错误的,对数组进行取地址是可以编译的。数组名可以隐式的退化成首个元素的指针,这才是右值。
C++11 开始
从 C++11 开始,为了配合移动语义,值的类别就不是左值右值这么简单了。
考虑一个简单的场景:
std::vector<int> a{...}; std::vector<int> b; b = a;我们知道第三行的赋值运算复杂度是正比于
a的长度的,复制的开销很大。但有些情况下,比如a在以后的代码中不会再使用,那么我们完全可以把a所持有的内存“转移”到b上,这就是移动语义干的事情。我们姑且不管移动是怎么实现的,先来考虑一下我们如何标记
a是可以移动的。显然不管能否移动,这个表达式的类型都是vector不变,所以只能对值类别下手。不可移动的a是左值,如果要在原有的体系下标记可以移动的a,我们只能把它标记为右值。但标记为右值又是不合理的,因为这个a实际上拥有自己的内存地址,与其他右值有有根本上的不同。所以 C++11 引入了 亡值 (xvalue) 这一值类别来标记这一种表达式。于是我们现在有了三种类别:左值 (lvalue)、纯右值 (prvalue)、亡值 (xvalue)(纯右值就是原先的右值)。
然后我们发现亡值同时具有一些左值和纯右值的性质,比如它可以像左值一样取地址,又像右值一样不会再被访问。
所以又有了两种组合类别:泛左值 (glvalue)(左值和亡值)、右值 (rvalue)(纯右值和亡值)。
……
关键的两个概念:
- 是否拥有身份 (identity):可以确定表达式是否与另一表达式指代同一实体,例如比较它们所标识的对象或函数的(直接或间接获得的)地址
- 是否可以被移动 (resources can be reused):对象的资源可以移动到别的对象中
这 5 种类型无非就是根据上面两种属性的是与否区分的,所以用下面的这张表格可以帮助理解:
拥有身份(glvalue) 不拥有身份 可移动(rvalue) xvalue prvalue 不可移动 lvalue 不存在 注意不拥有身份就意味着这个对象以后无法被访问,这样的对象显然是可以被移动的,所以不存在不拥有身份不可移动的值。
以上内容不需要完全理解「理解了对算法竞赛也没有太多用处」,但是至少,你大概明白前面说的左值、右值、亡值是什么了吧?而且你应该也猜出了:
++i既可以作为亡值也可以作为左值,即:既可以a=++i,也可以++i=a「但是其实++i=a中的i最后仍等于a」,并且可以给++i取地址:&(++i)。i++只能作为纯右值,不能作为左值,即:可以a=i++,但不可以i++=a,也不能&(i++)。「如果进行&(i++),编译器会报错:error: cannot take the address of an rvalue of type 'int'。这里的rvalue是prvalue的意思。」
所以,你甚至可以这样:int i=0;++i=++i+--i+i++-i---++i+ ++i- --i;。
猜猜最后 i 的值是多少?
参考资料
㉑ 运算符优先级问题「2022/11/10」
话说这么低级的问题已经好久没有遇到了,因为最简单的处理方式就是加括号。
但在今天正睿最后一场比赛中,竟然在这里栽跟头了……
简单来讲,T2 暴力是网络流中的最大流,于是打了个 dinic 暴力。
由于好久没有写网络流的板子,有些手生,调了半个小时才调好。考场写的 dinic 函数如下:
int dinic(int x,int flow)
{
if(x==n+2) return flow;
int rest=flow,k,i,y,w;
for(i=now[x];i&&rest;i=edge[i].next)
if(w=edge[i].w&&d[y=edge[i].to]==d[x]+1)
{
k=dinic(y,ly::min(rest,w));
if(!k) d[y]=0;
edge[i].w-=k,edge[i^1].w+=k,rest-=k;
}
now[x]=i;
return flow-rest;
}
一眼看上去没啥问题,良心出题人给的两个大样例都跑过了,于是放着每管。
结果考完悲愤地发现本来能拿 \(58pts\) 的 T2 爆零了……于是本来能上大分的我只上了小分。
自己随便造了几组小数据,测了一下没啥问题。无奈之下写了个数据生成器,跑了一下结果程序直接陷入死循环……
大概 debug 了快一个小时才锁定问题——dinic 函数中的条件判断:if(w=edge[i].w&&d[y=edge[i].to]==d[x]+1)。
竟然是运算符优先级问题!
- 我以为的:
if((w=edge[i].w)&&d[y=edge[i].to]==d[x]+1)。 - 实际上的:
if(w=(edge[i].w&&d[y=edge[i].to]==d[x]+1))!
也就是说,这里 w 被赋值为 edge[i].w&&d[y=edge[i].to]==d[x]+1 而不是 edge[i].w!
这就导致后面的 k=dinic(y,ly::min(rest,w)) 出错,从而陷入死循环。。。
很显然,问题在于:= 的优先级低于 &&。单独来看很好想到,但是放在一串式子的条件判断中,可能优先级问题就不是那么显然了。
这个教训在于,写一串表达式后一定要检查各个运算符的优先级,不确定的就加括号!
下面贴上C++ 运算符优先级总表,来源:【OI Wiki——运算】。
| 运算符 | 描述 | 例子 | 可重载性 |
|---|---|---|---|
| 第一级别 | |||
:: | 作用域解析符 | Class::age = 2; | 不可重载 |
| 第二级别 | |||
++ | 后自增运算符 | for (int i = 0; i < 10; i++) cout << i; | 可重载 |
-- | 后自减运算符 | for (int i = 10; i > 0; i--) cout << i; | 可重载 |
type() type{} | 强制类型转换 | unsigned int a = unsigned(3.14); | 可重载 |
() | 函数调用 | isdigit('1') | 可重载 |
[] | 数组数据获取 | array[4] = 2; | 可重载 |
. | 对象型成员调用 | obj.age = 34; | 不可重载 |
-> | 指针型成员调用 | ptr->age = 34; | 可重载 |
| 第三级别 (从右向左结合) | |||
++ | 前自增运算符 | for (i = 0; i < 10; ++i) cout << i; | 可重载 |
-- | 前自减运算符 | for (i = 10; i > 0; --i) cout << i; | 可重载 |
+ | 正号 | int i = +1; | 可重载 |
- | 负号 | int i = -1; | 可重载 |
! | 逻辑取反 | if (!done) … | 可重载 |
~ | 按位取反 | flags = ~flags; | 可重载 |
(type) | C 风格强制类型转换 | int i = (int) floatNum; | 可重载 |
* | 指针取值 | int data = *intPtr; | 可重载 |
& | 值取指针 | int *intPtr = &data; | 可重载 |
sizeof | 返回类型内存 | int size = sizeof floatNum; int size = sizeof(float); | 不可重载 |
new | 动态元素内存分配 | long *pVar = new long; MyClass *ptr = new MyClass(args); | 可重载 |
new [] | 动态数组内存分配 | long *array = new long[n]; | 可重载 |
delete | 动态析构元素内存 | delete pVar; | 可重载 |
delete [] | 动态析构数组内存 | delete [] array; | 可重载 |
| 第四级别 | |||
.* | 类对象成员引用 | obj.*var = 24; | 不可重载 |
->* | 类指针成员引用 | ptr->*var = 24; | 可重载 |
| 第五级别 | |||
* | 乘法 | int i = 2 * 4; | 可重载 |
/ | 除法 | float f = 10.0 / 3.0; | 可重载 |
% | 取余数(模运算) | int rem = 4 % 3; | 可重载 |
| 第六级别 | |||
+ | 加法 | int i = 2 + 3; | 可重载 |
- | 减法 | int i = 5 - 1; | 可重载 |
| 第七级别 | |||
<< | 位左移 | int flags = 33 << 1; | 可重载 |
>> | 位右移 | int flags = 33 >> 1; | 可重载 |
| 第八级别 | |||
<=> | 三路比较运算符 | if ((i <=> 42) < 0) ... | 可重载 |
| 第九级别 | |||
< | 小于 | if (i < 42) ... | 可重载 |
<= | 小于等于 | if (i <= 42) ... | 可重载 |
> | 大于 | if (i > 42) ... | 可重载 |
>= | 大于等于 | if (i >= 42) ... | 可重载 |
| 第十级别 | |||
== | 等于 | if (i == 42) ... | 可重载 |
!= | 不等于 | if (i != 42) ... | 可重载 |
| 第十一级别 | |||
& | 位与运算 | flags = flags & 42; | 可重载 |
| 第十二级别 | |||
^ | 位异或运算 | flags = flags ^ 42; | 可重载 |
| 第十三级别 | |||
| | 位或运算 | flags = flags | 42; | 可重载 |
| 第十四级别 | |||
&& | 逻辑与运算 | if (conditionA && conditionB) ... | 可重载 |
| 第十五级别 (从右向左结合) | |||
|| | 逻辑或运算 | if (conditionA || conditionB) ... | 可重载 |
| 第十六级别 (从右向左结合) | |||
? : | 条件运算符 | int i = a > b ? a : b; | 不可重载 |
throw | 异常抛出 | throw EClass("Message"); | 不可重载 |
= | 赋值 | int a = b; | 可重载 |
+= | 加赋值运算 | a += 3; | 可重载 |
-= | 减赋值运算 | b -= 4; | 可重载 |
*= | 乘赋值运算 | a *= 5; | 可重载 |
/= | 除赋值运算 | a /= 2; | 可重载 |
%= | 模赋值运算 | a %= 3; | 可重载 |
<<= | 位左移赋值运算 | flags <<= 2; | 可重载 |
>>= | 位右移赋值运算 | flags >>= 2; | 可重载 |
&= | 位与赋值运算 | flags &= new_flags; | 可重载 |
^= | 位异或赋值运算 | flags ^= new_flags; | 可重载 |
|= | 位或赋值运算 | flags |= new_flags; | 可重载 |
| 第十七级别 | |||
, | 逗号分隔符 | for (i = 0, j = 0; i < 10; i++, j++) ... | 可重载 |


 浙公网安备 33010602011771号
浙公网安备 33010602011771号