6-2 是否二叉搜索树(25 分)
本题要求实现函数,判断给定二叉树是否二叉搜索树。
函数接口定义:
bool IsBST ( BinTree T );
其中BinTree结构定义如下:
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
ElementType Data;
BinTree Left;
BinTree Right;
};
函数IsBST须判断给定的T是否二叉搜索树,即满足如下定义的二叉树:
定义:一个二叉搜索树是一棵二叉树,它可以为空。如果不为空,它将满足以下性质:
- 非空左子树的所有键值小于其根结点的键值。
- 非空右子树的所有键值大于其根结点的键值。
- 左、右子树都是二叉搜索树。
如果T是二叉搜索树,则函数返回true,否则返回false。
裁判测试程序样例:
#include <stdio.h>
#include <stdlib.h>
typedef enum { false, true } bool;
typedef int ElementType;
typedef struct TNode *Position;
typedef Position BinTree;
struct TNode{
ElementType Data;
BinTree Left;
BinTree Right;
};
BinTree BuildTree(); /* 由裁判实现,细节不表 */
bool IsBST ( BinTree T );
int main()
{
BinTree T;
T = BuildTree();
if ( IsBST(T) ) printf("Yes\n");
else printf("No\n");
return 0;
}
/* 你的代码将被嵌在这里 */
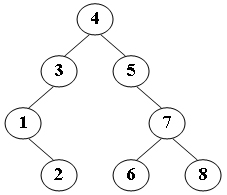
输入样例1:如下图
输出样例1:
Yes
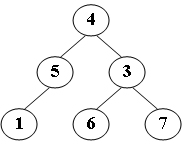
输入样例2:如下图
输出样例2:
No
代码;
bool IsBST ( BinTree T )
{
BinTree p;
if(!T)
return true;
if(!T->Left&&!T->Right)
return true;
p=T->Left;
if(p)
{
while(p->Right)//左子树的最大值在右下角
p=p->Right;
if(p->Data>T->Data)
return false;
}
p=T->Right;
if(p)
{
while(p->Left)//右子树的最小值在左下角
p=p->Left;
if(p->Data<T->Data)
return false;
}
return IsBST(T->Left)&&IsBST(T->Right);
}