Treap

基本概念

\(Treap\) 是一种形态平衡的二叉搜索树，也就是 平衡树 。因为其高度尽量平均，所以单次操作的时间复杂度会比普通的二叉搜索树更优。\(Treap\) 支持 二叉搜索树 的主要操作，并利用堆的性质来令树的形态更加的平衡，这也是其名字的由来 \(Tree + heap = treap\) 。

\(Treap\) 的代码通常会比较长，但是它的算法思想优美，并且性能也较为优秀。因此，\(Treap\) 可以说是一种非常实用的数据结构。

\(Treap\) 主要支持以下几种操作：

插入一个数 \(x\)
删除数 \(x\)，如果有多个 \(x\) ，只删除其中一个
查询 \(x\) 数的排名，排名定义为比当前数小的数的个数 \(+ 1\)。
查询排名为 \(x\) 的数
求 \(x\) 的前驱，前驱定义为比 \(x\) 小的最大的数
求 \(x\) 的后继，后继定义为比 \(x\) 大的最小的数

算法思想

旋转

\(Treap\) 的核心思想主要由左旋和右旋操作组成。

右旋的操作流程是：假如要对点 \(fa_x\) 进行右旋，且 \(x\) 是\(fa_x\) 的左儿子，那么 \(fa_x\) 就会成为点 \(x\) 的右儿子。此时若 \(x\) 原本有右儿子，则会发生冲突，所以还要令 \(x\) 原本的右儿子变成 \(fa_x\) 的左儿子。左旋的操作流程类似，只是把方向调换过来。具体见下图。

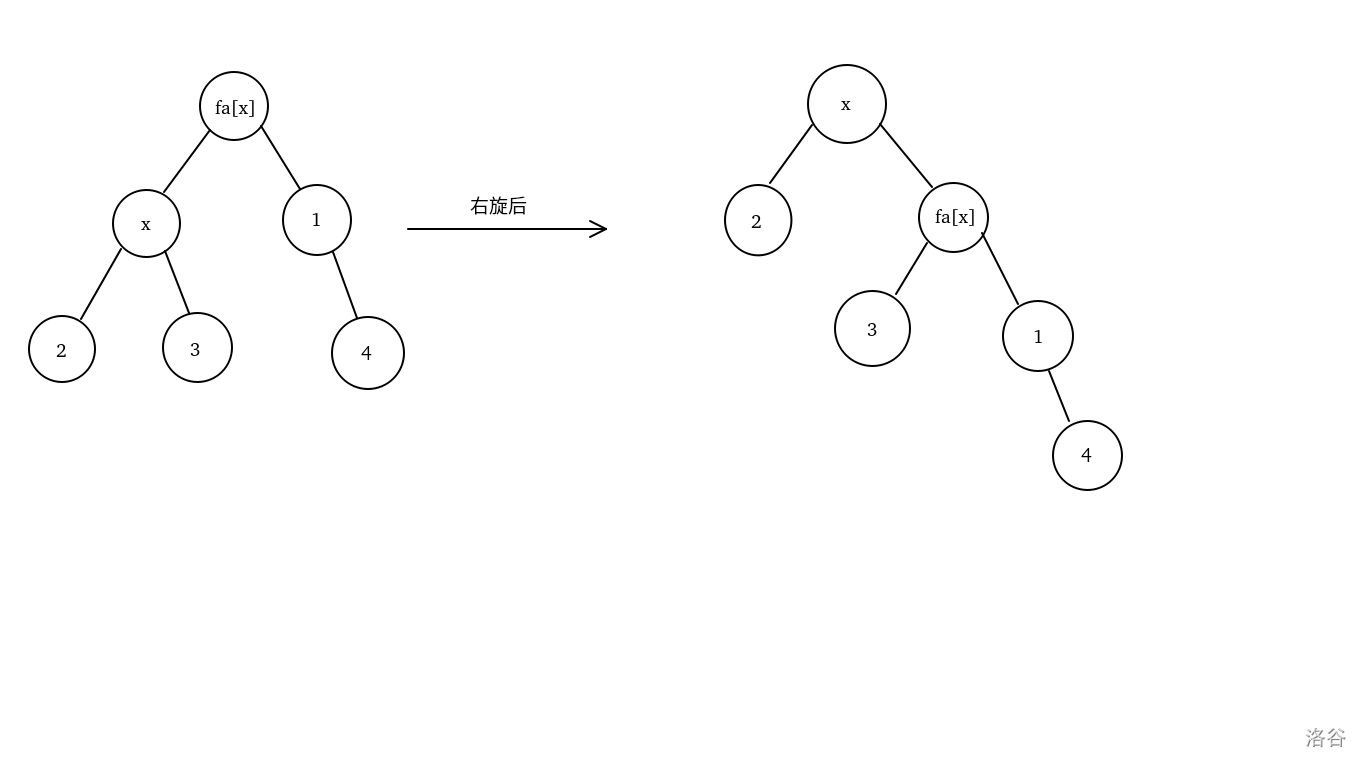
Treap右旋

显然，右旋或者左旋一次对二叉搜索树的性质并没有任何影响。由此，我们可以通过左旋和右旋来快速调整树的形态，从而配合堆的性质来令二叉搜索树尽量平衡。

除了二叉搜索树上的权值之外，我们还可以给每个节点加上一个随机的权值。接下来，我们利用左旋和右旋，将树的形态调整至满足如下性质：

对于原本的权值来说，这棵树必须满足二叉搜索树的性质，即节点 \(x\) 原本的权值一定大于其左子树中任意一个节点的原本权值且小于其右子树中任意一个节点的原本权值
对于随机权值来说，这棵树必须满足堆的性质，即节点 \(x\) 的随机权值比其两个子节点的随机权值都大或者都小，通常我们选用大根堆

注意到堆是一棵 完全二叉树，也就是说，假如我们令 \(Treap\) 满足以上条件，那么它既可以维护二叉搜索树的操作，又可以令层数尽量保持在 \(log n\) 层以内。这样令层数尽量平衡，操作的时间复杂度也会随之减少。

假如当前节点的随机权值大于其左儿子的随机权值，那么就右旋一次，把其左儿子旋转上来；假如当前节点的随机权值大于其右儿子的随机权值，那么就左旋一次，把其右儿子旋转上来。经过若干次操作，我们一定可以把 \(Treap\) 调整成想要的形态。

值得注意的是，因为旋转一次以后父子关系会发生变化，为了不再重新修改一次，我们在定义函数的时候需要加上取地址符，以确保存储儿子节点的数组也进行了相应的修改。也就是定义为 void rotate(int &p, int x)

插入

假如我们要在根节点为 \(p\) 的子树内插入一个数 \(x\) 。

若 \(p = 0\)，说明当前树中还不存在数 \(x\)，为 \(x\) 单独新开一个节点，并初始化即可。

若 \(p\) 的权值等于 \(x\)，说明要找的就是这一个节点。事先补充，因为可能会插入多次相同的数，所以相同的数直接存储在同一个节点中。所以，我们直接令 \(p\) 被插入的次数加一，子树大小也加一即可。

若 \(x\) 小于 \(p\) 的权值，说明 \(x\) 应该在 \(p\) 的左子树内，递归在左子树内插入 \(x\) 即可。\(x\) 大于 \(p\) 的情况同理。因为插入 \(x\) 后随机权值可能不满足堆的性质，所以如果修改的子节点就是 \(x\) 对应的节点，且 \(x\) 对应节点的随机权值大于当前节点的随机权值，直接进行相应的旋转即可。因为原来的随机权值一定满足堆的性质，若当前节点与其子节点不满足性质，只可能为当前节点是 \(x\) 的父节点，所以写代码时只需要判断随机权值的大小即可。

同理，函数定义为 void insert(int &p, int x)

删除

假如我们要在根节点为 \(p\) 的子树内删除一个数 \(x\) 。

若 \(p = 0\)，说明 \(x\) 在当前树内并不存在，直接结束。人

若 \(x\) 小于 \(p\) 的权值，说明 \(x\) 在 \(p\) 的左子树内，去 \(x\) 的左子树内删除即可。\(x\) 大于 \(p\) 的权值同理，去右子树内删除即可。

若 \(x\) 等于 \(p\) 的权值，说明 \(p\) 就是当前要删除的节点，继续分类讨论。若 \(p\) 是叶子节点，此时直接令 \(p\) 被插入的次数和子树大小减一即可，若删除后被插入的次数为 \(0\)，说明此时树中已经没有数 \(x\) 了，直接令 \(p = 0\) 以删除数 \(x\)。

若 \(p\) 只有左儿子而没有右儿子，直接对 \(p\) 进行右旋。此时的变量 p 已经在 rotate 函数中被赋值成了节点 \(x\) 的左儿子，而右旋一次过后，节点 \(x\) 的左儿子的右儿子已经被赋成了 \(x\)，再递归到 del(son[p][x], 1) 也就是递归到节点 \(p\) 了。这样把子节点全部旋转上去以后，直接删除节点 \(p\) 即可。\(p\) 只有右儿子而没有左儿子的情况同理，方向改变即可。这里分别给出两个对应的代码片段：

rotate(p, 1), del(son[p][1], x)

rotate(p, 0), del(son[p][0], x)

如果 \(p\) 拥有两个子节点，那么根据堆的性质，我们必须把随机权值较大的子节点旋转上来，以确保这棵平衡树的大根堆性质。我们将子节点旋转上来以后，直接去子节点对应的子树找到节点 \(p\) ，继续递归地查找，直到 \(p\) 变成叶子节点被删除为止。

同理，函数定义为 void del(int &p, int x)

其他操作

其他操作与二叉搜索树相同。

参考代码

例题链接

#include <cstdio>
#include <cstdlib>
#include <algorithm>
using namespace std;

const int maxn = 1e5 + 5;
const int inf = 0x3f3f3f3f;

int n, root, tot;
int size[maxn], son[maxn][2];
int val[maxn], cnt[maxn], rd[maxn];

inline int read() {
	int res = 0, flag = 1;
	char ch = getchar();
	while (ch < '0' || ch > '9') {
		if (ch == '-') {
			flag = -1;
		}
		ch = getchar();
	} 
	while (ch >= '0' && ch <= '9') {
		res = res * 10 + ch - '0';
		ch = getchar();
	}
	return res * flag;
}

inline void push_up(int p) {
	size[p] = size[son[p][0]] + size[son[p][1]] + cnt[p];
}

inline void rotate(int &p, int d) {
	int k = son[p][d ^ 1];
	son[p][d ^ 1] = son[k][d];
	son[k][d] = p;
	push_up(p);
	push_up(k);
	p = k;
}

inline void insert(int &p, int x) {
	if (!p) {
		p = ++tot;
		val[p] = x;
		size[p] = 1;
		cnt[p] = 1;
		rd[p] = rand();
		return;
	} else if (val[p] == x) {
		size[p]++;
		cnt[p]++;
		return;
	} else {
		int d = (x > val[p]);
		insert(son[p][d], x);
		if (rd[p] < rd[son[p][d]]) {
			rotate(p, d ^ 1);
		}
		push_up(p);
	}
}

inline void del(int &p, int x) {
	if (!p) {
		return;
	}
	if (x < val[p]) {
		del(son[p][0], x);
	} else if (x > val[p]) {
		del(son[p][1], x);
	} else {
		if (!son[p][0] && !son[p][1]) {
			size[p]--;
			cnt[p]--;
			if (cnt[p] == 0) {
				p = 0;
			}
		} else if (son[p][0] && !son[p][1]) {
			rotate(p, 1);
			del(son[p][1], x);
		} else if (!son[p][0] && son[p][1]) {
			rotate(p, 0);
			del(son[p][0], x);
		} else {
			int d = (rd[son[p][0]] > rd[son[p][1]]);
			rotate(p, d);
			del(son[p][d], x);
		}
	}
	push_up(p);
}

inline int rank(int p, int x) {
	if (!p) {
		return 1;
	} else if (val[p] == x) {
		return size[son[p][0]] + 1;
	} else if (val[p] > x) {
		return rank(son[p][0], x);
	} else {
		return size[son[p][0]] + cnt[p] + rank(son[p][1], x);
	}
}

inline int find(int p, int x) {
	if (!p) {
		return 0;
	} else if (size[son[p][0]] >= x) {
		return find(son[p][0], x);
	} else if (size[son[p][0]] + cnt[p] < x) {
		return find(son[p][1], x - size[son[p][0]] - cnt[p]);
	} else {
		return val[p];
	}
}

inline int pre(int p, int x) {
	if (!p) {
		return -inf;
	} else if (val[p] >= x) {
		return pre(son[p][0], x);
	} else {
		return max(val[p], pre(son[p][1], x));
	}
}

inline int nxt(int p, int x) {
	if (!p) {
		return inf;
	} else if (val[p] <= x) {
		return nxt(son[p][1], x);
	} else {
		return min(val[p], nxt(son[p][0], x));
	}
}

int main() {
	int opt, x;
	n = read();
	for (register int i = 1; i <= n; i++) {
		opt = read();
		x = read();
		if (opt == 1) {
			insert(root, x);
		} else if (opt == 2) {
			del(root, x);
		} else if (opt == 3) {
			printf("%d\n", rank(root, x));
		} else if (opt == 4) {
			printf("%d\n", find(root, x));
		} else if (opt == 5) {
			printf("%d\n", pre(root, x));
		} else {
			printf("%d\n", nxt(root, x));
		}
	}
	return 0;
}

posted @ 2021-07-24 23:30 kymru 阅读(79) 评论(0) 编辑收藏举报

刷新页面返回顶部

Loading

停更

Treap

基本概念

算法思想

旋转

插入

删除

其他操作

参考代码

公告