后缀数组
基本概念
后缀数组是处理字符串的有力工具。
后缀数组是一种处理字符串问题的算法。
后缀数组有多种实现,倍增后缀数组时间复杂度为 \(\mathcal{O}(n log n)\)。也可以 \(O(n)\) 做,但是很麻烦。
在这里约定下文(包括代码)中出现的字符串下标均从 \(1\) 开始,并且用后缀 \(i\) 来表示长度为 \(n\) 的字符串 \(S\) 从 \(i\) 到 \(n\) 的后缀。
算法思想
基本思想
后缀数组的算法思想:预处理出每一个后缀的排名,然后用不超过 \(\mathcal{O}(log n)\) 次排序将所有后缀按照字典序升序排列。使用 基数排序 来实现排序,时间复杂度为 \(\mathcal{O}(n log n)\)。
不妨设 \(rk_i\) 表示后缀 \(i\) 的排名,\(sa_i\) 表示排名为 \(i\) 的后缀首字母在字符串 \(S\) 中出现的位置。有一个性质是初始时 \(rk_{sa_i} = sa_{rk_i} = i\)。
我们主要考虑通过 倍增 的思想来更新 \(rk\)。设 \(rk_{w, i}\) 表示从 \(i\) 开始的长度为 \(w\) 的子串在字符串 \(S\) 所有长度为 \(w\) 的子串中的字典序排名。
假设现在我们已经求出 \(rk_{w, i}\),考虑 \(rk_{w, i}\) 可以更新的值。显然对于以 \(i\) 为开头的长度为 \(2 \times w\) 的子串,其前半段的字典序排名为 \(rk_{w, i}\),后半段的字典序排名为 \(rk_{w, i + w}\)。
不妨将 \(\forall 1 \leq i \leq n, rk_{w, i}\) 按照 \(rk_{w, i}\) 为第一关键字,\(rk_{w, i + w}\) 为第二关键字排序(如果 \(i + w > n, rk_{i + w} = -\infty\))。
一定有排序后 \(rk_{2 \times w, i}\) 等于 \((rk_{w, i}, rk_{w, i + w})\) 在 \(\forall 1 \leq i \leq n, (rk_{w, i}, rk_{w, i + w})\) 中的排名,也就是排序后的 离散化下标。由此我们可以在 \(\mathcal{O}(log n)\) 次排序内将字符串 \(S\) 的所有后缀按照字典序升序排列。初始时 \(rk_i = s_i\)。
感性理解:显然初始时我们直接令 \(rk_i = s_i\) 相当于把所有后缀按照第一个字符的字典序排序。因为可能会出现首字符相同的后缀,因此我们需要按照它们的第二个字符来排序。
因为后缀 \(i\) 的第二个字符实际上相当于后缀 \(i + 1\) 的首字符,而后缀 \(i + 1\) 的首字符排名我们已经求出为 \(rk_{1, i + 1}\),所以我们可以直接以 \(rk_{1, i}\) 为第一关键字,\(rk_{1, i + 1}\) 为第二关键字,相当于把每个后缀的前两个字符拆成两半,通过它们各自的排名计算出它们在所有后缀的长度为 \(2\) 的前缀中的排名。
经过排序,我们可以区分出部分首字符相同的后缀。同理,在第二次排序时我们需要把所有后缀按照前 \(4\) 个字符的字典序升序排序。对于以 \(i\) 开头的长度为 \(4\) 的后缀 \(i\) 之前缀,显然我们可以把它拆分成以 \(i\) 开头的长度为 \(2\) 的前缀和以 \(i + 2\) 开头的长度为 \(2\) 的前缀,然后通过第一次排序得到的排名来合并它们的排名。
因为我们在 \(i + w > n\) 时令 \(rk_{i + w} = -\infty\),所以我们可以看作是在原字符串的后面拼接了一个同样长度的字符串得到字符串 \(S^{\prime}\),这个字符串中的每一个子串字典序都是无穷小。
那么对于长度为 \(i\) 的后缀,我们实际上可以把它看作是字符串 \(S^{\prime}\) 以 \(i\) 开头的长度为 \(2^n - 1\) 的子串。这样每 \(i\) 轮倍增一定可以筛选出前 \(2^i\) 个字符相同的后缀,又因为所有后缀的长度不等,所以它们的字典序也不同,故而我们至多进行 \(\mathcal{O}(log n)\) 次排序就能把所有后缀按照字典序排序。
(下图源于 这篇题解,引用时略有改动。感谢 @Rainy7 绘制的图解。侵删)
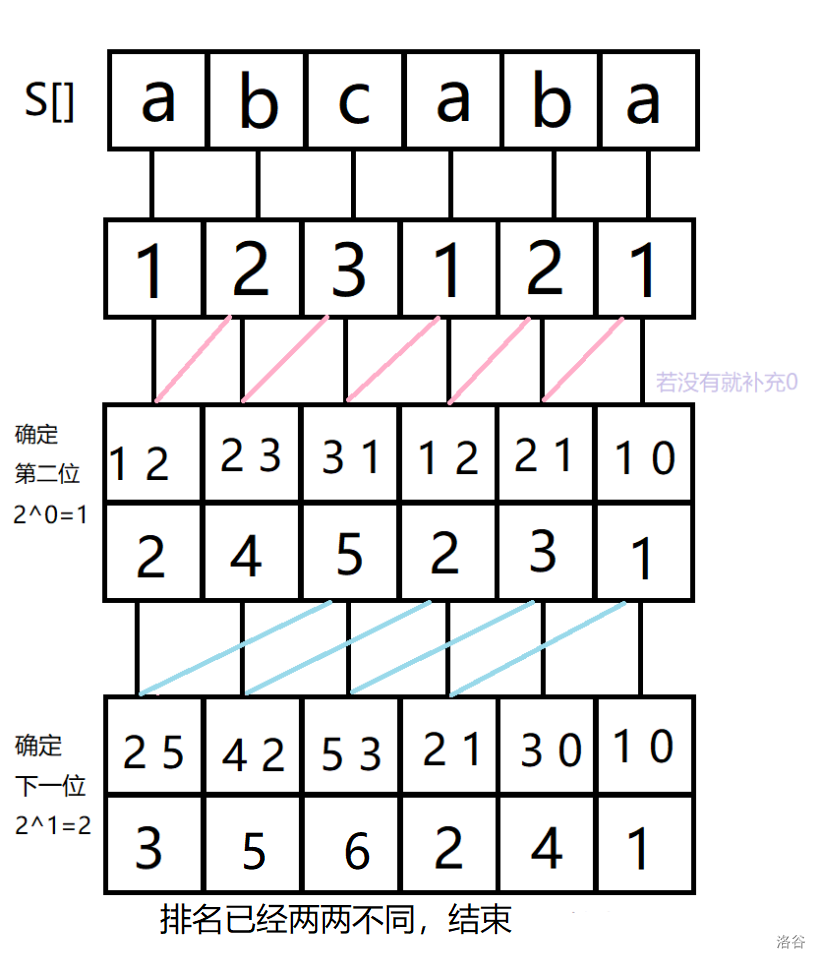
基数排序
基数排序是一种具有 稳定性 的排序算法,它的排序思想和桶排序类似。
假设现在我们有若干个包含 \(k\) 个关键字的元素,需要将其排序。那么我们可以先把这些元素按照第 \(k\) 关键字排序,再按第 \(k - 1\) 关键字排序……最后按照第 \(1\) 关键字排序。
每次排序我们会把所有元素按照当前关键字排序,又因为基数排序具有稳定性,所以当前关键字相同的元素一定会按照下一关键字有序。
具体的每一轮排序与桶排序类似。我们先统计出每一个关键字的出现次数,然后对其做前缀和。接着按照扫描一遍整个数组,每次把当前关键字的出现次数 \(- 1\) 的位置赋值为当前元素,然后令当前关键字的出现次数 \(- 1\)。
基数排序的时间复杂度为 \(\mathcal{O}(n)\),空间复杂度为值域范围。
参考代码(无卡常)
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn = 1e6 + 5;
const int maxv = 2e6 + 5;
int n, m;
int sa[maxn], id[maxn];
int cnt[maxn], rk[maxv], oldrk[maxv];
char s[maxn];
int main()
{
// freopen("P3809_8.in", "r", stdin);
// freopen("P3809_8.out", "w", stdout);
scanf("%s", s + 1);
n = strlen(s + 1);
m = max(n, 300);
for (int i = 1; i <= n; i++)
cnt[rk[i] = s[i]]++;
for (int i = 1; i <= m; i++)
cnt[i] += cnt[i - 1];
for (int i = n; i >= 1; i--)
sa[cnt[rk[i]]--] = i;
for (int j = 1; j < n; j <<= 1)
{
memset(cnt, 0, sizeof(cnt));
for (int i = 1; i <= n; i++)
id[i] = sa[i];
for (int i = 1; i <= n; i++)
cnt[rk[id[i] + j]]++;
for (int i = 1; i <= m; i++)
cnt[i] += cnt[i - 1];
for (int i = n; i >= 1; i--)
sa[cnt[rk[id[i] + j]]--] = id[i];
memset(cnt, 0, sizeof(cnt));
for (int i = 1; i <= n; i++)
id[i] = sa[i];
for (int i = 1; i <= n; i++)
cnt[rk[id[i]]]++;
for (int i = 1; i <= m; i++)
cnt[i] += cnt[i - 1];
for (int i = n; i >= 1; i--)
sa[cnt[rk[id[i]]]--] = id[i];
memcpy(oldrk, rk, sizeof(rk));
for (int p = 0, i = 1; i <= n; i++)
{
if (oldrk[sa[i]] == oldrk[sa[i - 1]] && oldrk[sa[i] + j] == oldrk[sa[i - 1] + j])
rk[sa[i]] = p;
else
rk[sa[i]] = ++p;
}
}
for (int i = 1; i <= n; i++)
printf("%d ", sa[i]);
return 0;
}
常数优化
由于 本人的代码常数大 倍增法实现的 \(SA\) 常数较大,您会发现如果将裸的模板交到洛谷 P3809 可以 \(AC\),但是在 LOJ#111 上大概率会 \(TLE\)。因此本文将介绍一些非常常见的卡常方法来帮助您卡过 \(SA\) 模板。亲测洛谷无常数优化与常数优化代码用时相差 \(4\) 到 \(5\) 倍。
基数排序
我们发现实际上第二关键字无需进行基数排序,原因是我们在代码中仅仅使用第二关键字统计了每一个排名的出现次数,所以关键字出现的顺序并无太大影响。我们可以先把 \(i + j > n\) 的所有 \(i\) 记录下来,然后再遍历一遍数组,\(\forall 1 \leq i \leq n, sa_i > j\),记录下 \(sa_i - j > 0\)。实现可以是这样的:
for (int i = n; i > n - j; i--)
id[++p] = i;
for (int i = 1; i <= n; i++)
if (sa[i] > j)
id[++p] = sa[i] - j;
优化值域
我们在离散化的过程中记录了累加变量 \(p\) 表示当前元素的离散化下标,那么每次排名的取值范围显然在 \([1, p]\)。我们每次排序后令 \(m = p\),从而优化枚举的值域。
优化不连续内存访问
我们在离散化的过程中会访问不连续的内存,这里可以用函数来判断:
bool cmp(int x, int y, int w)
{
return oldrk[x] == oldrk[y] && oldrk[x + w] == oldrk[y + w];
}
结束条件
如果每个后缀的排名都不一样说明后缀排序结束,那么此时的排名取值范围在 \([1, n]\) 之间,判断离散化下标是否等于 \(n\) 即可,是则直接退出。
参考代码(轻度卡常)
#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
const int maxn = 1e6 + 5;
const int maxm = 2e6 + 5;
int n, m;
int rk[maxm], oldrk[maxm];
int sa[maxn], id[maxn], cnt[maxn];
char s[maxn];
bool cmp(int x, int y, int w)
{
return oldrk[x] == oldrk[y] && oldrk[x + w] == oldrk[y + w];
}
int main()
{
int p = 0;
scanf("%s", s + 1);
// m 为基数排序的值域上限
// 理论上因为字符串 S 有 n 个后缀
// 所以后缀 i 在所有后缀中的字典序排名值域为 [1, n]
// 但是初始时我们用字符的 ASCII 码代表其排名
// 所以 m 的初始值应大于最大的可能出现的字符的 ASCII 码值
// 这里取 300,改为 114514 等数字均可
n = strlen(s + 1), m = 300;
for (int i = 1; i <= n; i++)
cnt[rk[i] = s[i]]++; // 等价于 rk[i] = s[i], cnt[rk[i]]++
for (int i = 1; i <= m; i++)
cnt[i] += cnt[i - 1];
for (int i = n; i >= 1; i--)
sa[cnt[rk[i]]--] = i; // 第一轮后缀排序
for (int j = 1; ; j <<= 1, m = p, p = 0)
{
for (int i = n; i > n - j; i--)
id[++p] = i;
for (int i = 1; i <= n; i++)
if (sa[i] > j)
id[++p] = sa[i] - j;
// 上面是是经过优化的代码,等价于下面这段代码
// 作用是以后缀 id[i] + j 的排名为第二关键字进行基数排序
// 后面要用 id 来更新 sa,因此不能直接用 sa 数组
// memset(cnt, 0, sizeof(cnt));
// for (int i = 1; i <= n; i++)
// id[i] = sa[i];
// for (int i = 1; i <= n; i++)
// cnt[rk[id[i] + j]]++;
// for (int i = 1; i <= m; i++)
// cnt[i] += cnt[i - 1];
// for (int i = n; i >= 1; i--)
// sa[cnt[rk[id[i] + j]]--] = id[i];
memset(cnt, 0, (m + 1) * sizeof(int));
// 按后缀 id[i] 的排名为第一关键字后缀排序
for (int i = 1; i <= n; i++)
cnt[rk[id[i]]]++;
for (int i = 1; i <= m; i++)
cnt[i] += cnt[i - 1];
for (int i = n; i >= 1; i--)
sa[cnt[rk[id[i]]]--] = id[i];
// 对 rk 的排序结果离散化
memcpy(oldrk, rk, sizeof(rk)), p = 0;
for (int i = 1; i <= n; i++)
rk[sa[i]] = cmp(sa[i], sa[i - 1], j) ? p : ++p;
if (p == n)
{
// 根据 sa[rk[i]] = i 来更新 sa
for (int i = 1; i <= n; i++)
sa[rk[i]] = i;
break;
}
}
for (int i = 1; i <= n; i++)
printf("%d ", sa[i]);
return 0;
}
\(LCP\)
基本概念
\(LCP\)(\(Longest\ Common\ Prefix\)),即最长公共前缀。在后缀数组一类的问题中,\(LCP(i, j)\) 定义为后缀 \(sa_i\) 和后缀 \(sa_j\) 的最长公共前缀。利用 \(LCP\) 及其性质可以方便地解决很多问题。
下面是一些比较基础的 \(LCP\) 性质及简单模板,由于本人水平有限故本文不涉及以下性质的证明。如果需要,可以参考 这篇博客。注意该博客仅供参考,如果不是我感觉不太行我就直接照抄了。
基本性质
- \(LCP(i, j) = LCP(j, i)\)
- \(LCP(i, i) = \operatorname{len}(sa_i) = n - i + 1\)
- \(LCP\ Lemma : \forall 1 \leq i \leq j \leq k \leq n, LCP(i, k) = \min\{LCP(i, j), LCP(j, k)\}\)
- \(LCP\ Theorem : \forall 1 \leq i < j \leq k, LCP(i, j) = \min\{LCP(j, j - 1)\}\)
其中 \(LCP\ Theorem\) 可以通过 \(LCP\ Lemma\) 得到。
例题讲解
给定您一个字符串 \(S\),试求 \(S\) 任意两个子串的 \(LCP\) 长度。
\(1 \leq |S| \leq 10^5\)
这道题可以用后缀数组来解决。先考虑这个问题的弱化版:对于给出的字符串 \(S\),求其任意两个 后缀 的 \(LCP\) 长度。
显然对于这个弱化版的问题,假设给出两个后缀分别是后缀 \(i\) 和后缀 \(j\),那么我们需要求的是 \(LCP(rk_i, rk_j)\)。不妨设 \(height_i = LCP(i, i - 1)\),那么根据 \(LCP\ Theorem\),后缀 \(i\) 和后缀 \(j\) 的 \(LCP\) 长度为 \(\forall i < k \leq j, height_k\)。这里可以使用 \(ST\) 表 \(O(log n)\) 实现。
考虑求出 \(height\)。不妨另设 \(x = rk_i, h_i = height_x\)。这里有另外一条重要的性质:
\(\forall 1 < i \leq n, h_i \geq h_{i - 1} - 1\)
那么我们可以像扩展 \(KMP\) 或者 \(manacher\) 一样 \(\mathcal{O}(n)\) 求解 \(h\) 数组再对应回 \(height\) 数组了。首先 \(h_{sa_1} = 0\),然后对于剩下的任意位置,我们可以确定 \(h_i \geq h_{i - 1}\)。不妨用一个变量实时记录下 \(h_{i - 1}\),每次从 \(h_{i - 1}\) 开始枚举 \(h_i\)。可以证明时间复杂度是 \(\mathcal{O}(n)\) 的。实现如下:
void get_height()
{
int k = 0;
for (int i = 1; i <= n; i++)
rk[sa[i]] = i;
for (int i = 1; i <= n; i++)
{
if (rk[i] == 1)
continue;
if (k) k--;
int j = sa[rk[i] - 1];
while (i + k <= n && j + k <= n && s[i + k] == s[j + k]) k++;
height[rk[i]] = k;
}
}
回到本题。我们发现如果情况够好,区间 \([x, y]\) 和区间 \([l, r]\) 的 \(LCP\) 长度应该等于后缀 \(x\) 和后缀 \(l\) 的 \(LCP\) 长度。但是由于后缀 \(x\) 和后缀 \(l\) 的 \(LCP\) 可能会超过给出的区间,因此答案还需要和两个区间的长度取较小值。
参考代码
#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
const int maxn = 1e5 + 5;
const int maxm = 2e5 + 5;
int n, m, q;
int rk[maxm], oldrk[maxm];
int height[maxn], f[maxn][20];
int sa[maxn], cnt[maxn], id[maxn];
char s[maxn];
bool cmp(int x, int y, int w)
{
return oldrk[x] == oldrk[y] && oldrk[x + w] == oldrk[y + w];
}
void get_height()
{
int k = 0;
for (int i = 1; i <= n; i++)
rk[sa[i]] = i;
for (int i = 1; i <= n; i++)
{
if (rk[i] == 1)
continue;
if (k) k--;
int j = sa[rk[i] - 1];
while (i + k <= n && j + k <= n && s[i + k] == s[j + k]) k++;
height[rk[i]] = k;
}
}
int get_log(int x)
{
int num = 1, res = 0;
while (num <= x)
{
num <<= 1;
res++;
}
return --res;
}
int query(int x, int y)
{
int len = get_log(y - x + 1);
return min(f[x][len], f[y - (1 << len) + 1][len]);
}
int main()
{
int x, y, l, r;
int ans, p = 0;
scanf("%s", s + 1);
n = strlen(s + 1), m = 300;
for (int i = 1; i <= n; i++)
cnt[rk[i] = s[i]]++;
for (int i = 1; i <= m; i++)
cnt[i] += cnt[i - 1];
for (int i = n; i >= 1; i--)
sa[cnt[rk[i]]--] = i;
for (int j = 1; ; j <<= 1, m = p, p = 0)
{
for (int i = n; i > n - j; i--)
id[++p] = i;
for (int i = 1; i <= n; i++)
if (sa[i] > j)
id[++p] = sa[i] - j;
memset(cnt, 0, (m + 1) * sizeof(int));
for (int i = 1; i <= n; i++)
cnt[rk[id[i]]]++;
for (int i = 1; i <= m; i++)
cnt[i] += cnt[i - 1];
for (int i = n; i >= 1; i--)
sa[cnt[rk[id[i]]]--] = id[i];
memcpy(oldrk, rk, sizeof(rk)), p = 0;
for (int i = 1; i <= n; i++)
rk[sa[i]] = cmp(sa[i], sa[i - 1], j) ? p : ++p;
if (p == n)
{
for (int i = 1; i <= n; i++)
sa[rk[i]] = i;
break;
}
}
get_height();
for (int i = 1; i <= n; i++)
f[i][0] = height[i];
for (int j = 1; (1 << j) <= n; j++)
for (int i = 1; i + (1 << j) - 1 <= n; i++)
f[i][j] = min(f[i][j - 1], f[i + (1 << (j - 1))][j - 1]);
scanf("%d", &q);
for (int i = 1; i <= q; i++)
{
scanf("%d%d%d%d", &x, &y, &l, &r);
if (x == l)
{
printf("%d\n", min(y, r) - x + 1);
continue;
}
int rkx = rk[x], rkl = rk[l];
if (rkx > rkl)
swap(l, x), swap(r, y), swap(rkx, rkl);
ans = min(min(y - x + 1, r - l + 1), query(rkx + 1, rkl));
printf("%d\n", ans);
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号