Splay
概念
Splay 是一种 平衡树 ,由 \(Daniel \ Sleator\) 和 \(Robert \ Tarjan\) 提出。
Splay 利用 旋转 ,与 Treap 不同的地方在于 Splay 不会给每个结点另外附上一个随机权值,而是在每一次操作过后将被操作的结点旋转到根结点,在此过程中顺便维护树的平衡。
操作
注意对“结点0”的操作
清空
清空某个结点的所有信息。
void clear(int x) {
son[x][0] = son[x][1] = size[x] = val[x] = cnt[x] = fa[x] = 0;
}
更新
更新结点 \(x\) 的子树大小。
void update(int x) {
if (x) {
size[x] = cnt[x];
if (son[x][0]) {
size[x] += size[son[x][0]];
}
if (son[x][1]) {
size[x] += size[son[x][1]];
}
}
}
判断左/右儿子
判断结点 \(x\) 是其父亲的左儿子还是右儿子。
bool get(int x) {
return son[fa[x]][1] == x;
}
双旋
分类讨论三种情况:
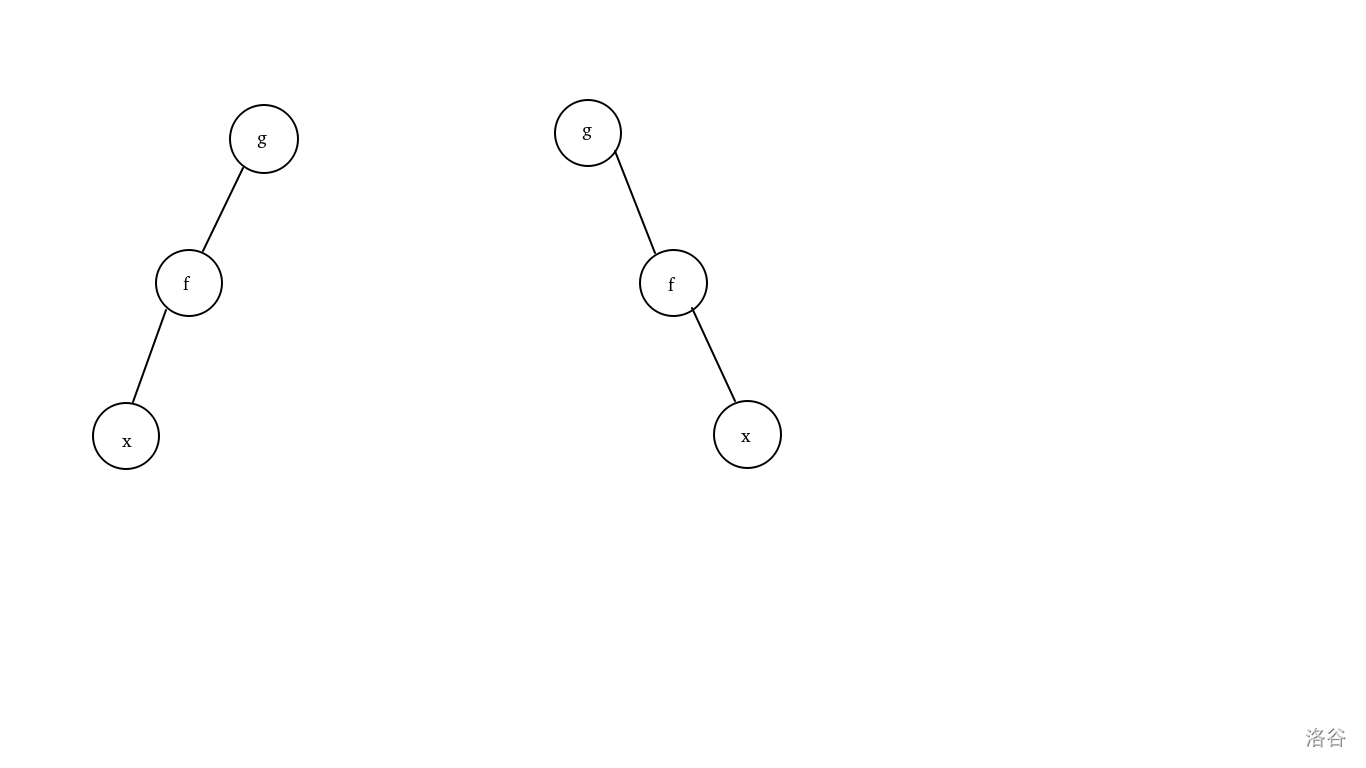
假如我们要将 \(x\) 旋转到 \(g\) 的位置。令当前结点为 \(x\) ,其父结点为 \(f\) ,祖先结点为 \(g\) 。
如果 \(x\) 是 \(f\) 的左儿子,且 \(f\) 也是 \(g\) 的左儿子;或者 \(x\) 是 \(f\) 的右儿子,且 \(f\) 也是 \(g\) 的右儿子,即父子方向统一:
则此时先旋转 \(f\) ,再旋转 \(x\)
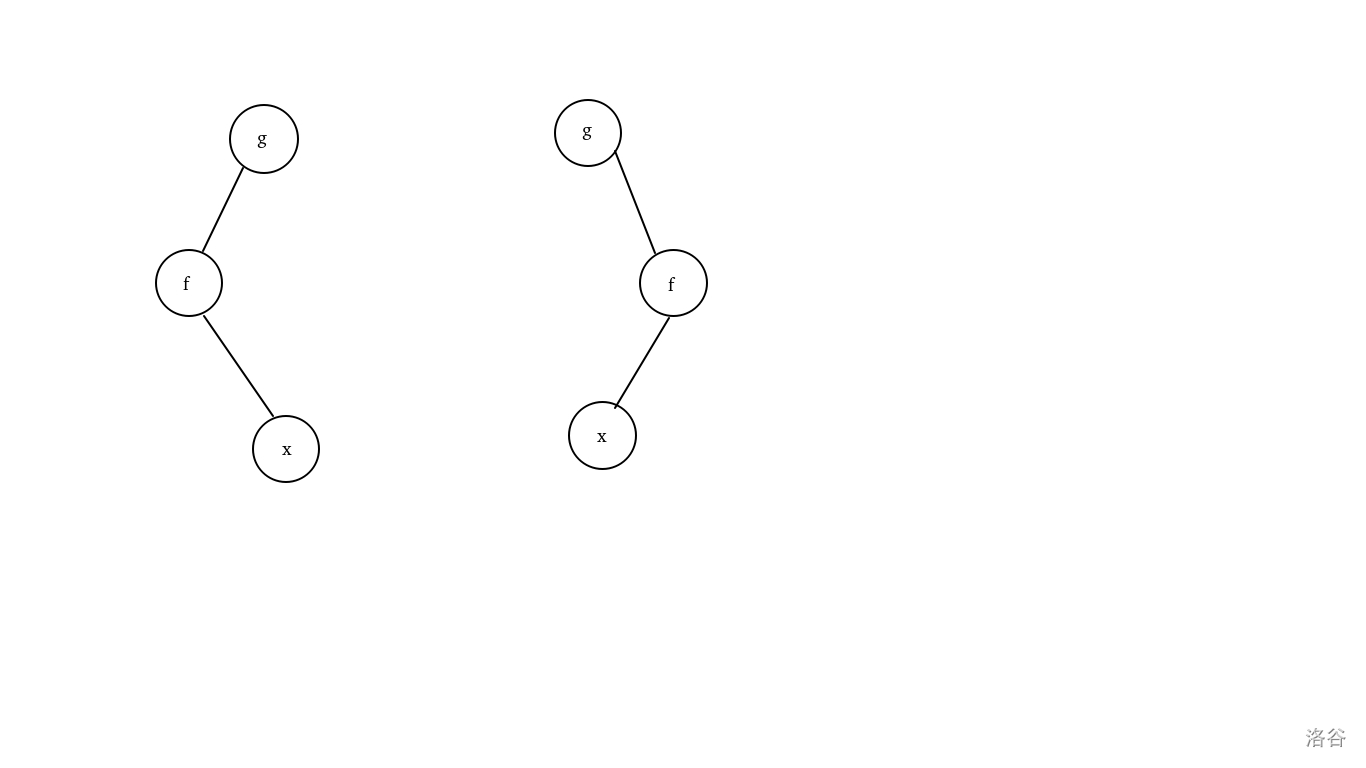
如果 \(x\) 是 \(f\) 的右儿子,且 \(f\) 是 \(g\) 的左儿子;或者 \(x\) 是 \(f\) 的左儿子,且 \(f\) 是 \(g\) 的右儿子,即父子方向不统一:
此时先将 \(x\) 旋转到 \(f\) 的位置,再从 \(f\) 的位置旋转到 \(g\) 的位置即可。
最后,如果 \(f\) 就是根结点,此时不需要双旋,直接单旋 \(x\) 到根结点的位置即可。
void rotate(int x) {
int y = fa[x], z = fa[y], k = get(x);
son[y][k] = son[x][k ^ 1];
fa[son[y][k]] = y;
son[x][k ^ 1] = y;
fa[y] = x;
fa[x] = z;
if (z) {
son[z][son[z][1] == y] = x;
}
update(y);
update(x);
}
伸展
Splay 操作即为将某个结点 \(x\) 一路向上旋转,直到成为另一个结点 \(goal\) 的子结点。
可以将 Splay 操作拆分成多次双旋操作。
具体地,假设当前结点为 \(x\) ,若 \(x\) 的父亲结点和祖先结点都不是 \(goal\) ,此时直接进行双旋操作即可。
若 \(x\) 的祖先结点为 \(goal\) ,说明此时直接进行一次单旋即可。
若 \(x\) 的父亲结点为 \(goal\) ,说明 \(x\) 已经是 \(goal\) 的子结点了,直接退出。
void splay(int x, int goal) {
for (int f; (f = fa[x]) != goal; rotate(x)) {
if (fa[f] != goal) {
rotate(get(x) == get(f) ? f : x);
}
}
if (!goal) {
root = x;
}
}
插入
在树中插入一个值为 \(x\) 的新结点。
假如全树的根结点 \(root = 0\) ,说明这棵树是空树,新建一个结点并将其设为根结点即可。
否则,从根结点开始查找。若当前结点的权值等于 \(x\) ,说明之前已经插入过值相同的结点,令其个数加一,并更新该结点及其父结点,并将该结点伸展到根结点即可。
反之,在相应的子树内查找。如果此时发现该子树为空树,说明该值在树中并不存在,直接新建一个结点,更新其父结点并将其旋转到根结点。
void insert(int x) {
if (root == 0) {
tot++;
val[tot] = x;
cnt[tot] = size[tot] = 1;
son[tot][0] = son[tot][1] = fa[tot] = 0;
root = tot;
return;
}
int u = root, f = 0;
while (true) {
if (x == val[u]) {
cnt[u]++;
update(u);
update(f);
splay(u);
break;
}
f = u;
u = son[u][x > val[u]];
if (u == 0) {
tot++;
fa[tot] = f;
son[tot][0] = son[tot][1] = 0;
son[f][x > val[f]] = tot;
cnt[tot] = size[tot] = 1;
val[tot] = x;
update(f);
splay(tot);
break;
}
}
}
排名
查询值 \(x\) 在树中的排名。
常见的查询排名写法。
int rank(int x) {
int u = root, ans = 0;
while (true) {
if (!u) return ans + 1;
if (x < val[u]) {
u = son[u][0];
} else {
if (son[u][0]) {
ans += size[son[u][0]];
}
if (x == val[u]) {
splay(u);
return ans + 1;
}
ans += cnt[u];
u = son[u][1];
}
}
}
查找
查找树中排名为 \(x\) 的值的编号。
假如当前结点的左子树不为空并且左子树的大小 \(\geq x\) ,在左子树内继续查找;
否则,若 \(x \leq\) 左子树的大小加上当前结点的个数,直接返回当前结点的编号;
反之,令排名减去左子树的大小 \(+\) 当前结点的个数,继续在右子树内查找。
int find(int x) {
int u = root;
while (true) {
if (son[u][0] && x <= size[son[u][0]]) {
u = son[u][0];
} else {
int sz = (son[u][0] ? size[son[u][0]] : 0) + cnt[u];
if (x <= sz) {
return val[u];
}
x -= sz;
u = son[u][1];
}
}
}
前驱、后继
查找树中 \(x\) 的前驱的编号。
不管树中是否存在 \(x\),先将 \(x\) 插入到树中,并将 \(x\) 旋转到根结点。此时 \(x\) 的左子树一定全部小于 \(x\) ,右子树一定全部大于 \(x\)。前驱就是左子树内右下角的结点,后继就是右子树内左下角的结点。
注意最后还要删去 \(x\) 。
int pre() {
int u = son[root][0];
while (son[u][1]) {
u = son[u][1];
}
return u;
}
//调用入口
//insert(x);
//printf("%d\n", val[pre()]);
//del(x);
int nxt() {
int u = son[root][1];
while (son[u][0]) {
u = son[u][0];
}
return u;
}
//调用入口
//insert(x);
//printf("%d\n", val[nxt()]);
//del(x);
删除
删除树中值为 \(x\) 的结点,若有多个,只删一个。
先利用 rank 函数将 \(x\) 旋转到根结点,再分类讨论:
-
如果 \(x\) 被多次插入,删除其中一个并更新即可;
-
如果 \(x\) 是叶子节点,直接清空 \(x\) 并将 \(root\) 赋值为 \(0\) 表示删除后是空树;
-
如果 \(x\) 只有左儿子,将左儿子赋为新根并清空 \(x\),只有右儿子同理;
-
反之,将 \(x\) 的前驱伸展到根结点,左子树其他的结点不动,再将 \(x\) 的右子树连接在前驱的右子树上。直接清空 \(x\) 并更新。
void del(int x) {
rank(x);
if (cnt[root] > 1) {
cnt[root]--;
update(root);
return;
}
if (!son[root][0] && !son[root][1]) {
clear(root);
root = 0;
return;
}
if (!son[root][0]) {
int rt = root;
root = son[root][1];
fa[root] = 0;
clear(rt);
return;
}
if (!son[root][1]) {
int rt = root;
root = son[root][0];
fa[root] = 0;
clear(rt);
return;
}
int p = pre(), rt = root;
splay(p);
son[root][1] = son[rt][1];
fa[son[rt][1]] = root;
clear(rt);
update(root);
}
代码
#include <cstdio>
using namespace std;
#define rank Rank
const int maxn = 1e5 + 5;
int n, root, tot;
int fa[maxn], son[maxn][2];
int cnt[maxn], val[maxn], size[maxn];
void clear(int x) {
son[x][0] = son[x][1] = size[x] = val[x] = cnt[x] = fa[x] = 0;
}
bool get(int x) {
return son[fa[x]][1] == x;
}
void update(int x) {
if (x) {
size[x] = cnt[x];
if (son[x][0]) {
size[x] += size[son[x][0]];
}
if (son[x][1]) {
size[x] += size[son[x][1]];
}
}
}
void rotate(int x) {
int y = fa[x], z = fa[y], k = get(x);
son[y][k] = son[x][k ^ 1];
fa[son[y][k]] = y;
son[x][k ^ 1] = y;
fa[y] = x;
fa[x] = z;
if (z) {
son[z][son[z][1] == y] = x;
}
update(y);
update(x);
}
void splay(int x) {
for (int f = 0; (f = fa[x]); rotate(x)) {
if (fa[f]) {
rotate((get(x) == get(f)) ? f : x);
}
}
root = x;
}
void insert(int x) {
if (root == 0) {
tot++;
val[tot] = x;
cnt[tot] = size[tot] = 1;
son[tot][0] = son[tot][1] = fa[tot] = 0;
root = tot;
return;
}
int u = root, f = 0;
while (true) {
if (x == val[u]) {
cnt[u]++;
update(u);
update(f);
splay(u);
break;
}
f = u;
u = son[u][x > val[u]];
if (u == 0) {
tot++;
fa[tot] = f;
son[tot][0] = son[tot][1] = 0;
son[f][x > val[f]] = tot;
cnt[tot] = size[tot] = 1;
val[tot] = x;
update(f);
splay(tot);
break;
}
}
}
int rank(int x) {
int u = root, ans = 0;
while (true) {
if (!u) return ans + 1;
if (x < val[u]) {
u = son[u][0];
} else {
if (son[u][0]) {
ans += size[son[u][0]];
}
if (x == val[u]) {
splay(u);
return ans + 1;
}
ans += cnt[u];
u = son[u][1];
}
}
}
int find(int x) {
int u = root;
while (true) {
if (son[u][0] && x <= size[son[u][0]]) {
u = son[u][0];
} else {
int sz = (son[u][0] ? size[son[u][0]] : 0) + cnt[u];
if (x <= sz) {
return val[u];
}
x -= sz;
u = son[u][1];
}
}
}
int pre() {
int u = son[root][0];
while (son[u][1]) {
u = son[u][1];
}
return u;
}
int nxt() {
int u = son[root][1];
while (son[u][0]) {
u = son[u][0];
}
return u;
}
void del(int x) {
rank(x);
if (cnt[root] > 1) {
cnt[root]--;
update(root);
return;
}
if (!son[root][0] && !son[root][1]) {
clear(root);
root = 0;
return;
}
if (!son[root][0]) {
int rt = root;
root = son[root][1];
fa[root] = 0;
clear(rt);
return;
}
if (!son[root][1]) {
int rt = root;
root = son[root][0];
fa[root] = 0;
clear(rt);
return;
}
int p = pre(), rt = root;
splay(p);
son[root][1] = son[rt][1];
fa[son[rt][1]] = root;
clear(rt);
update(root);
}
int main() {
int opt, x;
scanf("%d", &n);
while (n--) {
scanf("%d%d", &opt, &x);
if (opt == 1) {
insert(x);
} else if (opt == 2) {
del(x);
} else if (opt == 3) {
printf("%d\n", rank(x));
} else if (opt == 4) {
printf("%d\n", find(x));
} else if (opt == 5) {
insert(x);
printf("%d\n", val[pre()]);
del(x);
} else {
insert(x);
printf("%d\n", val[nxt()]);
del(x);
}
}
return 0;
}
例题
文艺平衡树
请写出一个可以翻转区间的数据结构。
建一棵按照下标平衡的二叉树,每个结点存储下标对应的值,同时利用 Splay 的性质来调整结点顺序。
显然,无论我们如何旋转,最终按照中序遍历都会依次遍历下标为 \(1\) 的值,下标为 \(2\) 的值……下标为 \(n\) 的值。所以,我们可以交换下标对应的值,从而达到区间翻转的效果。
当我们要旋转区间 \([l, r]\) 的时候,我们需要找到 \(l - 1\) 和 \(r + 1\) 对应的结点,并将 \(l - 1\) 对应的结点伸展到根结点,将 \(r + 1\) 对应的结点旋转成 \(l - 1\) 的右儿子。
此时,\(r + 1\) 的左子树一定包含区间 \([l, r]\) 对应的结点。令 \(r + 1\) 的左儿子为 \(k\) ,此时给 \(k\) 打上 \(lazy\) 标记,表示区间 \([l, r]\) 需要翻转,并交换 \(k\) 的左右子树。
文艺平衡树可以线段树一样建树即可。注意要加入两个权值分别为 \(-\infty\) 和 \(\infty\) 的结点。方便翻转区间 \([1, n]\) 。每次可能导致左右儿子发生变化的时候,都要先下传 \(lazy\) 标记。
#include <cstdio>
#include <algorithm>
using namespace std;
const int maxn = 1e5 + 5;
const int inf = 0x3f3f3f3f;
int n, m, root, tot;
int a[maxn], val[maxn], fa[maxn], lazy[maxn];
int son[maxn][2], size[maxn];
bool get(int x) {
return son[fa[x]][1] == x;
}
void update(int x) {
if (x) {
size[x] = 1;
if (son[x][0]) {
size[x] += size[son[x][0]];
}
if (son[x][1]) {
size[x] += size[son[x][1]];
}
}
}
void push_down(int x) {
if (x && lazy[x]) {
lazy[son[x][0]] ^= 1;
lazy[son[x][1]] ^= 1;
swap(son[x][0], son[x][1]);
lazy[x] = 0;
}
}
void rotate(int x) {
int y = fa[x], z = fa[y], k = get(x);
son[y][k] = son[x][k ^ 1];
fa[son[y][k]] = y;
son[x][k ^ 1] = y;
fa[y] = x;
fa[x] = z;
if (z) {
son[z][son[z][1] == y] = x;
}
update(y);
update(x);
}
void splay(int x, int goal) {
for (int f; (f = fa[x]) != goal; rotate(x)) {
if (fa[f] != goal) {
rotate(get(f) == get(x) ? f : x);
}
}
if (goal == 0) {
root = x;
}
}
int build(int l, int r, int f) {
if (l > r) {
return 0;
}
int mid = (l + r) / 2;
int now = ++tot;
fa[now] = f;
son[now][0] = son[now][1] = 0;
val[now] = a[mid];
size[now] = 1;
son[now][0] = build(l, mid - 1, now);
son[now][1] = build(mid + 1, r, now);
update(now);
return now;
}
int find(int x) {
int now = root;
while (true) {
push_down(now);
if (x <= size[son[now][0]]) {
now = son[now][0];
} else {
x -= (size[son[now][0]] + 1);
if (!x) {
return now;
}
now = son[now][1];
}
}
}
void reverse(int x, int y) {
int l = x - 1, r = y + 1;
l = find(l);
r = find(r);
splay(l, 0);
splay(r, l);
int now = son[root][1];
now = son[now][0];
lazy[now] ^= 1;
}
void dfs(int now) {
push_down(now);
if (son[now][0]) {
dfs(son[now][0]);
}
if (val[now] != inf && val[now] != -inf) {
printf("%d ", val[now]);
}
if (son[now][1]) {
dfs(son[now][1]);
}
}
int main() {
int l, r;
scanf("%d%d", &n, &m);
a[1] = -inf;
for (int i = 1; i <= n; i++) {
a[i + 1] = i;
}
a[n + 2] = inf;
root = build(1, n + 2, 0);
for (int i = 1; i <= m; i++) {
scanf("%d%d", &l, &r);
reverse(l + 1, r + 1);
}
dfs(root);
return 0;
}
区间插入问题
给定一个长度为 \(n\) 的序列 \(a\) 和 \(m\) 次操作,每次操作可以:
-
把数 \(s\) 调整到序列开头
-
把数 \(s\) 调整到序列结尾
-
把数 \(s\) 向右移动 \(t\) 位
-
查询数 \(s\) 前的数值数量
-
查询序列中第 \(s\) 个数
文艺平衡树。
前三种操作的本质都是一样的。这几种操作都需要先在文艺平衡树中删除 \(s\) ,然后再分别在 \(2, n + 1\) 和 \(s\) 原本的位置 \(+ t\) 处重新插入 \(s\) 。
考虑在文艺平衡树中维护结点对应的下标和数值对应的结点,在代码中分别使用 val 和 pos 来表示。
假如需要在序列 \(k\) 的位置插入数值为 \(k\) 的结点,那么可以先找出文艺平衡树中下标为 \(x\) 和 \(x - 1\) 的结点,并把 \(x\) 结点旋转到根,\(x - 1\) 结点旋转成 \(x\) 的左儿子。
此时 \(x - 1\) 一定没有右儿子,并且 \(k\) 结点刚好可以插入在 \(x - 1\) 的右儿子处。此时在 \(x - 1\) 的右儿子处新建结点,之后相应地更新结点信息。
考虑维护第四种操作。实际上是询问文艺平衡树中 \(s\) 对应的结点的左子树大小 \(- 1\) 。我们可以直接找到 \(s\) 对应的结点,并把它旋转到根,最后返回根结点的左子树大小 \(- 1\) 即可。直接用 pos 查询。
第五种操作实际上是询问文艺平衡树中排名为 \(s + 1\) 的结点的值,直接改一下 find 就行。
#include <cstdio>
using namespace std;
const int maxn = 2e6 + 5;
int n, m, root, tot;
int a[maxn], size[maxn], son[maxn][2];
int fa[maxn], val[maxn], pos[maxn], cnt[maxn];
char opt[maxn];
void clear(int x)
{
size[x] = son[x][0] = son[x][1] = fa[x] = cnt[x] = 0;
pos[val[x]] = 0, val[x] = 0;
}
bool get(int x)
{
return son[fa[x]][1] == x;
}
void push_up(int x)
{
if (x)
{
size[x] = cnt[x];
if (son[x][0])
size[x] += size[son[x][0]];
if (son[x][1])
size[x] += size[son[x][1]];
}
}
void rotate(int x)
{
int y = fa[x], z = fa[y], k = get(x);
son[y][k] = son[x][k ^ 1];
fa[son[y][k]] = y;
son[x][k ^ 1] = y;
fa[y] = x;
fa[x] = z;
if (z)
son[z][son[z][1] == y] = x;
push_up(y);
push_up(x);
}
void splay(int x, int goal)
{
for (int f; (f = fa[x]) != goal; rotate(x))
if (fa[f] != goal)
rotate(get(x) == get(f) ? f : x);
if (!goal)
root = x;
}
int build(int l, int r, int f)
{
if (l > r)
return 0;
int mid = (l + r) / 2, u = ++tot;
fa[u] = f;
size[u] = cnt[u] = 1;
val[u] = a[mid];
pos[a[mid]] = u;
son[u][0] = build(l, mid - 1, u);
son[u][1] = build(mid + 1, r, u);
push_up(u);
return u;
}
int pre()
{
int u = son[root][0];
while (son[u][1])
u = son[u][1];
return u;
}
int rank(int x)
{
splay(pos[x], 0);
return size[son[root][0]] + 1;
}
int find(int x)
{
int u = root;
while (true)
{
if (son[u][0] && x <= size[son[u][0]])
u = son[u][0];
else
{
int sz = (son[u][0] ? size[son[u][0]] : 0) + cnt[u];
if (x <= sz)
return u;
x -= sz;
u = son[u][1];
}
}
}
void del(int x)
{
rank(x);
if (cnt[root] > 1)
{
cnt[root]--;
push_up(root);
return;
}
else if (!son[root][0] && !son[root][1])
{
clear(root);
root = 0;
return;
}
else if (!son[root][1])
{
int rt = root;
root = son[root][0];
fa[root] = 0;
clear(rt);
return;
}
else if (!son[root][0])
{
int rt = root;
root = son[root][1];
fa[root] = 0;
clear(rt);
return;
}
else
{
int p = pre(), rt = root;
splay(p, 0);
son[root][1] = son[rt][1];
fa[son[root][1]] = root;
clear(rt);
push_up(root);
return;
}
}
void update(int idx, int value)
{
int x = find(idx), y = find(idx - 1);
splay(x, 0);
splay(y, x);
son[y][1] = ++tot;
fa[tot] = y;
size[tot] = cnt[tot] = 1;
son[tot][0] = son[tot][1] = 0;
val[tot] = value;
pos[value] = tot;
push_up(y);
push_up(x);
}
int main()
{
int s, t, x;
scanf("%d%d", &n, &m);
a[1] = 0;
for (int i = 1; i <= n; i++)
scanf("%d", &a[i + 1]);
a[n + 2] = n + 1;
root = build(1, n + 2, 0);
for (int i = 1; i <= m; i++)
{
scanf("%s", opt);
if (opt[0] == 'T')
{
scanf("%d", &s);
del(s);
update(2, s);
}
else if (opt[0] == 'B')
{
scanf("%d", &s);
del(s);
update(n + 1, s);
}
else if (opt[0] == 'I')
{
scanf("%d%d", &s, &t);
x = rank(s);
del(s);
update(x + t, s);
}
else if (opt[0] == 'A')
{
scanf("%d", &s);
printf("%d\n", rank(s) - 2);
}
else
{
scanf("%d", &s);
printf("%d\n", val[find(s + 1)]);
}
}
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号