对于一类数据范围较小的 规划 / 分配 / 调整求最值问题,可以考虑建图用网络流处理。
可以和优化建图等手段一起使用。
memset 的时候要 注意范围 (点的个数)。
概念
流网络:一个包含点集和边集的有向图 G = ( V , E ) G = ( V , E ) ( u , v ) ( u , v ) c ( u , v ) c ( u , v ) s s t t
净流:边 ( u , v ) ( u , v ) ( u , v ) ( u , v ) ( v , u ) ( v , u )
可行流:记 f ( u , v ) f ( u , v ) ( u , v ) ( u , v )
容量限制:0 ≤ f ( u , v ) ≤ c ( u , v ) 0 ≤ f ( u , v ) ≤ c ( u , v )
流守恒:除 u = s u = s u = t u = t ∑ x ∈ V f ( u , x ) = ∑ x ∈ V f ( x , t ) ∑ x ∈ V f ( u , x ) = ∑ x ∈ V f ( x , t )
流量值:令 f f | f | | f | | f | = ∑ ( s , v ) ∈ E f ( s , v ) − ∑ ( v , s ) ∈ E f ( v , s ) | f | = ∑ ( s , v ) ∈ E f ( s , v ) − ∑ ( v , s ) ∈ E f ( v , s )
残量网络(残留网络):残量网络总是针对原图中某一可行流而言,因此残量网络可以视作可行流的一个函数,通常记为 G f = ( V f , E f ) G f = ( V f , E f ) V f = V V f = V E f E f E E E E c ′ ( u , v ) c ′ ( u , v )
c ′ ( u , v ) = { c ( u , v ) − f ( u , v ) ( u , v ) ∈ E f ( v , u ) ( v , u ) ∈ E c ′ ( u , v ) = { c ( u , v ) − f ( u , v ) ( u , v ) ∈ E f ( v , u ) ( v , u ) ∈ E
最大流(最大可行流):图中流量值最大的可行流。
增广路径:残量网络中从源点 s s t t
割:网络中顶点的一种划分,把所有顶点划分成两个顶点集合 S S T T s ∈ S , t ∈ T s ∈ S , t ∈ T S ∪ T = V , S ∩ T = ∅ S ∪ T = V , S ∩ T = ∅ ( S , T ) ( S , T )
割的容量:定义割 ( S , T ) ( S , T ) c ( S , T ) = ∑ u ∈ S , v ∈ T c ( u , v ) c ( S , T ) = ∑ u ∈ S , v ∈ T c ( u , v ) c ( s , t ) c ( s , t )
最小割:图中容量最小的割。
最大流
P3376 【模板】网络最大流
求最大流可以用 Edmonds-Karp, Dinic, ISAP, HLPP Edmonds-Karp, Dinic, ISAP, HLPP
E d m o n d s − K a r p E d m o n d s − K a r p 即 E K E K
E K E K
每次找到一条增广路,假设该增广路上最小的剩余容量为 k k k k k k
直接在原图中找增广路会导致结果不是最大流,原因是找增广路时可能会先遍历到较劣方案,而减去边权会对残量网络造成影响。解决方法是在原图中添加初始容量为 0 0 k k
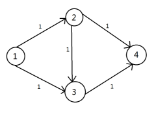
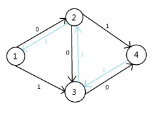
以下图为例,源点为 1 1 4 4 E K E K
最坏情况下会找到增广路 1 , 2 , 3 , 4 1 , 2 , 3 , 4 1 1
如果没有反向边,此时已经无法找到增广路,得到最大流为 1 1 2 2 1 , 3 , 2 , 4 1 , 3 , 2 , 4 1 1
此时残量网络中无增广路,算法结束,得到最大流为 2 2
图中的反向边起到反悔作用。当选择第一条增广路后,我们发现实际上有更优的做法。所以通过 3 → 2 3 → 2 1 1 2 2 1 , 2 , 4 1 , 2 , 4 1 1 3 , 4 3 , 4 1 , 3 , 4 1 , 3 , 4 1 1
E K E K O ( m 2 n ) O ( m 2 n )
view code #include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
using namespace std;
typedef long long ll;
const int maxn = 205 ;
const int maxm = 1e4 + 5 ;
const ll inf = 1e18 ;
struct node {
int to, nxt;
ll w;
} edge[maxm];
int n, m, s, t;
int cnt = 1 ;
int head[maxn], pre[maxn];
ll ans;
ll dis[maxn];
ll val[maxn][maxn];
bool vis[maxn];
void add_edge (int u, int v, ll w) bool bfs () int > q;
memset (vis, false , (n + 1 ) * sizeof (bool ));
vis[s] = true ;
dis[s] = inf;
q.push (s);
while (!q.empty ()) {
int u = q.front ();
q.pop ();
for (int i = head[u]; i; i = edge[i].nxt) {
int v = edge[i].to;
if ((edge[i].w == 0 ) || vis[v]) {
continue ;
}
dis[v] = min (dis[u], edge[i].w);
pre[v] = i;
if (v == t) {
return true ;
}
vis[v] = true ;
q.push (v);
}
}
return false ;
}
void update () int cur = t;
while (cur != s) {
edge[pre[cur]].w -= dis[t];
edge[pre[cur] ^ 1 ].w += dis[t];
cur = edge[pre[cur] ^ 1 ].to;
}
ans += dis[t];
}
int main () int u, v;
ll w;
scanf ("%d%d%d%d" , &n, &m, &s, &t);
for (int i = 1 ; i <= m; i++) {
scanf ("%d%d%lld" , &u, &v, &w);
val[u][v] += w;
}
for (int i = 1 ; i <= n; i++) {
for (int j = 1 ; j <= n; j++) {
if (val[i][j]) {
add_edge (i, j, val[i][j]);
add_edge (j, i, 0 );
}
}
}
while (bfs ()) {
update ();
}
printf ("%lld\n" , ans);
return 0 ;
}
D i n i c D i n i c D i n i c D i n i c E K E K
我们发现 E K E K
前置知识:分层图
这里的分层图不是将原图复制成若干份,而是将原图划分成若干个层次。
令 d u d u s s u u d v = d u + 1 d v = d u + 1
不妨先在残量网络上进行 b f s b f s ∀ ( u , v ) ∈ E f ∀ ( u , v ) ∈ E f d v = d u + 1 d v = d u + 1 v v t t
当前弧优化:显然一条边在搜索结束后不会再次对答案产生影响,因此可以记录下当前顶点访问到的边。下一次访问该顶点直接从这条边开始搜索即可。
时间复杂度 O ( n 2 m ) O ( n 2 m )
D i n i c D i n i c O ( m √ n ) O ( m n )
view code #include <cstdio>
#include <cstring>
#include <queue>
using namespace std;
typedef long long ll;
const int maxn = 205 ;
const int maxm = 1e4 + 5 ;
const ll inf = 1e18 ;
struct node {
int to, nxt;
ll w;
} edge[maxm];
int n, m, s, t;
int cnt = 1 ;
int head[maxn], cur[maxn], dep[maxn];
ll ans;
ll val[maxn][maxn];
void add_edge (int u, int v, ll w) bool bfs () int > q;
memset (dep, 0 , (n + 1 ) * sizeof (int ));
dep[s] = 1 ;
q.push (s);
while (!q.empty ()) {
int u = q.front ();
q.pop ();
for (int i = head[u]; i; i = edge[i].nxt) {
int v = edge[i].to;
if ((dep[v] == 0 ) && (edge[i].w > 0 )) {
dep[v] = dep[u] + 1 ;
q.push (v);
}
}
}
if (dep[t] > 0 ) {
return true ;
}
return false ;
}
ll dfs (int u, ll dis) {
if (u == t) {
return dis;
}
for (int &i = cur[u]; i; i = edge[i].nxt) {
int v = edge[i].to;
if ((dep[v] == dep[u] + 1 ) && (edge[i].w > 0 )) {
ll dist = dfs (v, min (dis, edge[i].w));
if (dist > 0 ) {
edge[i].w -= dist;
edge[i ^ 1 ].w += dist;
return dist;
}
}
}
return 0 ;
}
void dinic () while (bfs ()) {
ll dis;
for (int i = 1 ; i <= n; i++) {
cur[i] = head[i];
}
while (dis = dfs (s, inf)) {
ans += dis;
}
}
}
int main () int u, v;
ll w;
scanf ("%d%d%d%d" , &n, &m, &s, &t);
for (int i = 1 ; i <= m; i++) {
scanf ("%d%d%lld" , &u, &v, &w);
val[u][v] += w;
}
for (int i = 1 ; i <= n; i++) {
for (int j = 1 ; j <= n; j++) {
if (val[i][j]) {
add_edge (i, j, val[i][j]);
add_edge (j, i, 0 );
}
}
}
dinic ();
printf ("%lld\n" , ans);
return 0 ;
}
I S A P I S A P I S A P I S A P D i n i c D i n i c D i n i c D i n i c D i n i c D i n i c I S A P I S A P
类似地,从汇点 t t b f s b f s d u = d v + 1 d u = d v + 1 ( u , v ) ( u , v ) u u 1 1
当源点的层次大于点数时,说明已经无法找到合法的增广路,算法结束。
g a p g a p g a p i g a p i i i k k g a p k = 0 g a p k = 0 k k k k t t
同样地,I S A P I S A P
view code #include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
using namespace std;
typedef long long ll;
const int maxn = 205 ;
const int maxm = 1e4 + 5 ;
const ll inf = 1e18 ;
struct node {
int to, nxt;
ll w;
} edge[maxm];
int n, m, s, t;
int cnt = 1 ;
int head[maxn], cur[maxn], dep[maxn], gap[maxn];
ll ans;
void add_edge (int u, int v, ll w) void bfs () int > q;
memset (dep, -1 , sizeof (dep));
memset (gap, 0 , sizeof (gap));
dep[t] = 0 ;
gap[0 ] = 1 ;
q.push (t);
while (!q.empty ()) {
int u = q.front ();
q.pop ();
for (int i = head[u]; i; i = edge[i].nxt) {
int v = edge[i].to;
if (dep[v] == -1 ) {
dep[v] = dep[u] + 1 ;
gap[dep[v]]++;
q.push (v);
}
}
}
}
ll dfs (int u, ll flow) {
if (u == t) {
ans += flow;
return flow;
}
ll used = 0 ;
for (int &i = cur[u]; i; i = edge[i].nxt) {
int v = edge[i].to;
if (edge[i].w && (dep[v] + 1 == dep[u])) {
ll val = dfs (v, min (flow - used, edge[i].w));
if (val) {
edge[i].w -= val;
edge[i ^ 1 ].w += val;
used += val;
}
if (used == flow) {
return flow;
}
}
}
gap[dep[u]]--;
if (!gap[dep[u]]) {
dep[s] = n + 1 ;
}
dep[u]++;
gap[dep[u]]++;
return used;
}
void isap () bfs ();
while (dep[s] < n) {
memcpy (cur, head, (n + 1 ) * sizeof (int ));
dfs (s, inf);
}
}
int main () int u, v;
ll w;
scanf ("%d%d%d%d" , &n, &m, &s, &t);
for (int i = 1 ; i <= m; i++) {
scanf ("%d%d%lld" , &u, &v, &w);
add_edge (u, v, w);
add_edge (v, u, 0 );
}
isap ();
printf ("%lld\n" , ans);
return 0 ;
}
H L P P H L P P 最高标号预流推进(High Level Preflow Push, HLPP High Level Preflow Push, HLPP
假设顶点 u u h u h u h s = n , h t = 0 h s = n , h t = 0 t t ∀ ( u , v ) ∈ E ∀ ( u , v ) ∈ E h u = h v + 1 h u = h v + 1 H L P P H L P P
假设当前顶点 u u u u h u = min ( h v + 1 ) h u = min ( h v + 1 ) ( u , v ) ∈ E ( u , v ) ∈ E n + 1 n + 1
每次用队列保存需要推送流量的顶点,每次推送完当前顶点的流量后将与其相邻的顶点加入队列。将队列换成优先队列就是 H L P P H L P P
g a p g a p I S A P I S A P H L P P H L P P g a p g a p u u k k u u k k ∀ h i > k ∀ h i > k h i = n + 1 h i = n + 1
该算法的时间复杂度是 O ( n 2 √ m ) O ( n 2 m )
view code #include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
using namespace std;
const int maxn = 1.2e3 + 5 ;
const int maxm = 1.2e5 + 5 ;
const int inf = 0x3f3f3f3f ;
struct node {
int to, nxt, w;
} edge[maxm << 1 ];
int n, m, s, t;
int cnt = 1 ;
int head[maxn], h[maxn], flow[maxn], gap[maxn << 1 ];
bool vis[maxn];
struct cmp {
bool operator () (int a, int b) const return (h[a] < h[b]);
}
};
priority_queue<int , vector<int >, cmp> pq;
void add_edge (int u, int v, int w) bool bfs () int > q;
memset (h, 0x3f , (n + 1 ) * sizeof (int ));
h[t] = 0 ;
q.push (t);
while (!q.empty ()) {
int u = q.front ();
q.pop ();
for (int i = head[u]; i; i = edge[i].nxt) {
int v = edge[i].to;
if (edge[i ^ 1 ].w && (h[v] > h[u] + 1 )) {
h[v] = h[u] + 1 ;
q.push (v);
}
}
}
return (h[s] != inf);
}
void push (int u) for (int i = head[u]; i; i = edge[i].nxt) {
int v = edge[i].to;
if (edge[i].w && (h[v] + 1 == h[u])) {
int val = min (flow[u], edge[i].w);
edge[i].w -= val;
edge[i ^ 1 ].w += val;
flow[u] -= val;
flow[v] += val;
if ((v != s) && (v != t) && (!vis[v])) {
pq.push (v);
vis[v] = true ;
}
if (!flow[u]) {
break ;
}
}
}
}
void relabel (int u) for (int i = head[u]; i; i = edge[i].nxt) {
int v = edge[i].to;
if (edge[i].w) {
h[u] = min (h[u], h[v] + 1 );
}
}
}
void hlpp () if (!bfs ()) {
return ;
}
h[s] = n;
memset (gap, 0 , (n << 1 ) * sizeof (int ));
for (int i = 1 ; i <= n; i++) {
if (h[i] != inf) {
gap[h[i]]++;
}
}
for (int i = head[s]; i; i = edge[i].nxt) {
int v = edge[i].to;
if (edge[i].w) {
int cur = edge[i].w;
edge[i].w -= cur;
edge[i ^ 1 ].w += cur;
flow[s] -= cur;
flow[v] += cur;
if ((v != s) && (v != t) && (!vis[v])) {
pq.push (v);
vis[v] = true ;
}
}
}
while (!pq.empty ()) {
int u = pq.top ();
pq.pop ();
vis[u] = false ;
push (u);
if (flow[u]) {
gap[h[u]]--;
if (!gap[h[u]]) {
for (int i = 1 ; i <= n; i++) {
if ((i != s) && (i != t) && (h[i] > h[u]) && (h[i] < n + 1 )) {
h[i] = n + 1 ;
}
}
}
relabel (u);
gap[h[u]]++;
pq.push (u);
vis[u] = true ;
}
}
}
int main () int u, v, w;
scanf ("%d%d%d%d" , &n, &m, &s, &t);
for (int i = 1 ; i <= m; i++) {
scanf ("%d%d%d" , &u, &v, &w);
add_edge (u, v, w);
add_edge (v, u, 0 );
}
hlpp ();
printf ("%d\n" , flow[t]);
return 0 ;
}
最小割
最小割最大流(Max-flow Min-cut Max-flow Min-cut G G
对于网络 G G f f ( S , T ) ( S , T ) t t ∑ u ∈ S , v ∈ T f ( u , v ) − f ( v , u ) ∑ u ∈ S , v ∈ T f ( u , v ) − f ( v , u ) S S T T ∑ u ∈ S , v ∈ T c ( u , v ) ∑ u ∈ S , v ∈ T c ( u , v )
显然任一割的容量等于最大流流量时取最小值,则我们可以构造一个符合条件的割:在原图中跑完最大流后,将 s s S S T T ( S , T ) ( S , T ) S S T T ∑ u ∈ S , v ∈ T f ( u , v ) − f ( v , u ) = c ( u , v ) ∑ u ∈ S , v ∈ T f ( u , v ) − f ( v , u ) = c ( u , v )
综上所述,对于任意网络 G G
费用流
简介
P3381 【模板】最小费用最大流
给定一个包含 n n m m G = ( V , E ) G = ( V , E ) 1 1 n n 1 1 m m s s t t w ( u , v ) w ( u , v ) c ( u , v ) c ( u , v )
试给每条边 ( u , v ) ( u , v ) f ( u , v ) f ( u , v )
每条边的流量不超过其流量限制
除源点和汇点外,每个点流入的流量和流出的流量相等
源点流出的流量等于汇点流入的流量
定义网络 G G F ( G ) = ∑ ( s , i ) ∈ E f ( s , i ) F ( G ) = ∑ ( s , i ) ∈ E f ( s , i ) C ( G ) = ∑ ( i , j ) ∈ E f ( i , j ) × c ( i , j ) C ( G ) = ∑ ( i , j ) ∈ E f ( i , j ) × c ( i , j )
求该网络的最小费用最大流,即在 F ( G ) F ( G ) C ( G ) C ( G )
S P F A S P F A S P F A S P F A E K E K
对于原图中的边 ( u , v ) ( u , v ) 0 0 − c ( u , v ) − c ( u , v ) E K E K b f s b f s S P F A S P F A
原理:
显然增广的顺序不影响最大流的值。因为求最短路实质是找增广路,且算法会在程序中无增广路时结束,因此该算法求出的 F ( G ) F ( G )
该算法每次增广一条残量网络中的最短路,因此总是贪心地做出当前最优的选择。当贪心不影响其后的最短路时,显然局部最优可以导致全局最优。反之,因为建边时反向边的边权(单位流量的花费)为其正向边的相反数,所以之后找到的最短路可以通过这条边返还若干个单位流量,同时相应地撤销其花费。类似于最大流,这些流量实际上是被两条不同的增广路接管了。通过反向边,我们确定贪心可以反悔,因此该算法求出的 C ( G ) C ( G )
综上所述,该算法求出的是最小费用最大流。
当然,该算法也可以套 S P F A S P F A D i n i c D i n i c
view code #include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
using namespace std;
typedef long long ll;
const int maxn = 5e3 + 5 ;
const int maxm = 1e5 + 5 ;
const ll inf = 1e18 ;
struct node {
int to, nxt;
ll w, c;
} edge[maxm];
int n, m, s, t;
int cnt = 1 , mc, mf;
int head[maxn], cur[maxn];
ll dis[maxn];
bool in_queue[maxn], vis[maxn];
void add_edge (int u, int v, ll w, ll c) bool spfa () int > q;
for (int i = 1 ; i <= n; i++) {
dis[i] = inf;
}
memset (in_queue, false , (n + 1 ) * sizeof (bool ));
dis[s] = 0 ;
in_queue[s] = true ;
q.push (s);
while (!q.empty ()) {
int u = q.front ();
q.pop ();
in_queue[u] = false ;
for (int i = head[u]; i; i = edge[i].nxt) {
int v = edge[i].to;
if ((edge[i].w > 0 ) && (dis[v] > dis[u] + edge[i].c)) {
dis[v] = dis[u] + edge[i].c;
if (!in_queue[v]) {
in_queue[v] = true ;
q.push (v);
}
}
}
}
return (dis[t] != inf);
}
ll dfs (int u, ll flow) {
if (u == t) {
mf += flow;
return flow;
}
ll sum = 0 ;
vis[u] = true ;
for (int &i = cur[u]; i; i = edge[i].nxt) {
int v = edge[i].to;
if ((edge[i].w > 0 ) && (dis[v] == dis[u] + edge[i].c) && (!vis[v])) {
ll val = dfs (v, min (flow, edge[i].w));
edge[i].w -= val;
edge[i ^ 1 ].w += val;
mc += edge[i].c * val;
sum += val;
flow -= val;
if (!flow) {
break ;
}
}
}
vis[u] = false ;
return sum;
}
void dinic () while (spfa ()) {
memcpy (cur, head, (n + 1 ) * sizeof (int ));
dfs (s, inf);
}
}
int main () int u, v;
ll w, c;
scanf ("%d%d%d%d" , &n, &m, &s, &t);
for (int i = 1 ; i <= m; i++) {
scanf ("%d%d%lld%lld" , &u, &v, &w, &c);
add_edge (u, v, w, c);
add_edge (v, u, 0 , -c);
}
dinic ();
printf ("%lld %lld\n" , mf, mc);
return 0 ;
}
z k w z k w 思想
z k w z k w K M K M
回顾最短路算法中的距离标号。定义 D i D i i i ( u , v ) ∈ E ( u , v ) ∈ E
D v ≤ D u + w ( u , v ) D v ≤ D u + w ( u , v )
对于每一个 v v u u
在 z k w z k w D u = D v + c ( u , v ) D u = D v + c ( u , v ) 1 1 2 2 K M K M
对于最后一次找增广路失败的 d f s d f s V V d = min i ∈ V , j ∉ V ( c ( i , j ) − D i + D j ) d = min i ∈ V , j ∉ V ( c ( i , j ) − D i + D j ) d d
分析
个人理解为 z k w z k w d = min i ∈ V , j ∉ V c ( i , j ) − D i + D j d = min i ∈ V , j ∉ V c ( i , j ) − D i + D j j j D i D i i i j j d d t t
根据上文,当 t t D i = D j + c i j D i = D j + c i j D i D i i i t t D s D s 1 1 t t f l o w f l o w D s × f l o w D s × f l o w f l o w f l o w
经过大量实测,z k w z k w
不妨从算法角度分析一下。z k w z k w K M K M S P F A S P F A z k w z k w
z k w z k w K M K M
由此看来,z k w z k w z k w z k w z k w z k w
view code #include <cstdio>
#include <cstring>
#include <deque>
using namespace std;
const int maxn = 5e3 + 5 ;
const int maxm = 1e5 + 5 ;
const int inf = 2147483647 ;
struct node {
int to, nxt, w, c;
} edge[maxm];
int n, m, s, t;
int cnt = 1 , max_flow, min_cost;
int head[maxn], dis[maxn];
bool vis[maxn];
void add_edge (int u, int v, int w, int c) int dfs (int u, int flow) if (u == t) {
max_flow += flow;
min_cost += dis[s] * flow;
return flow;
}
vis[u] = true ;
int used = 0 ;
for (int i = head[u]; i; i = edge[i].nxt) {
int v = edge[i].to;
if ((!vis[v]) && edge[i].w && (dis[u] == dis[v] + edge[i].c)) {
int cur = dfs (v, min (flow, edge[i].w));
if (cur) {
edge[i].w -= cur;
edge[i ^ 1 ].w += cur;
used += cur;
if (used == flow) {
return flow;
}
}
}
}
return used;
}
bool relabel () int d = inf;
for (int u = 1 ; u <= n; u++) {
if (vis[u]) {
for (int i = head[u]; i; i = edge[i].nxt) {
int v = edge[i].to;
if (!vis[v] && edge[i].w) {
d = min (d, dis[v] - dis[u] + edge[i].c);
}
}
}
}
if (d == inf) {
return false ;
}
for (int i = 1 ; i <= n; i++) {
if (vis[i]) {
dis[i] += d;
}
}
return true ;
}
void zkw () do {
do {
memset (vis, false , (n + 1 ) * sizeof (bool ));
} while (dfs (s, inf));
} while (relabel ());
}
int main () int u, v, w, c;
scanf ("%d%d%d%d" , &n, &m, &s, &t);
for (int i = 1 ; i <= m; i++) {
scanf ("%d%d%d%d" , &u, &v, &w, &c);
add_edge (u, v, w, c);
add_edge (v, u, 0 , -c);
}
zkw ();
printf ("%d %d\n" , max_flow, min_cost);
return 0 ;
}
原始对偶
当 h ( u 1 ) h ( u 1 ) h ( u k ) h ( u k ) l l l − h ( u 1 ) + h ( u k ) l − h ( u 1 ) + h ( u k )
考虑势函数 h h ∀ 1 ≤ i ≤ n , h ( i ) = 0 ∀ 1 ≤ i ≤ n , h ( i ) = 0 S P F A S P F A h h
每次找最短路结束后,令新图上从源点 s s i i d i s i d i s i ∀ 1 ≤ i ≤ n ∀ 1 ≤ i ≤ n i i h ( i ) = h ( i ) + d i s i h ( i ) = h ( i ) + d i s i
每次增广结束后原图中会加入一些边 ( v , u ) ( v , u ) d i s u + w ′ ( u , v ) = d i s v d i s u + w ′ ( u , v ) = d i s v
d i s u + w ′ ( u , v ) = d i s v d i s u + w ( u , v ) + h ( u ) − h ( v ) = d i s v ( d i s v + h ( v ) ) − ( d i s u + h ( u ) ) − w ( u , v ) = 0 ( d i s v + h ( v ) ) − ( d i s u + h ( u ) ) + w ( v , u ) = 0 d i s u + w ′ ( u , v ) = d i s v d i s u + w ( u , v ) + h ( u ) − h ( v ) = d i s v ( d i s v + h ( v ) ) − ( d i s u + h ( u ) ) − w ( u , v ) = 0 ( d i s v + h ( v ) ) − ( d i s u + h ( u ) ) + w ( v , u ) = 0
因此对于新加入的边,这样修改势函数仍然满足势函数的性质。
对于 G ′ G ′ ( u , v ) ( u , v ) d i s u + w ′ ( u , v ) ≥ d i s v d i s u + w ′ ( u , v ) ≥ d i s v
d i s u + w ′ ( u , v ) − d i s v ≥ 0 d i s u + w ( u , v ) − d i s v + h ( u ) − h ( v ) ≥ 0 ( d i s u + h ( u ) ) − ( d i s v + h ( v ) ) + w ( u , v ) ≥ 0 d i s u + w ′ ( u , v ) − d i s v ≥ 0 d i s u + w ( u , v ) − d i s v + h ( u ) − h ( v ) ≥ 0 ( d i s u + h ( u ) ) − ( d i s v + h ( v ) ) + w ( u , v ) ≥ 0
因此对于 G ′ G ′
由此可以得到算法的流程:
初始化 h h
在根据残量网络构建的新图中跑 D i j k s t r a D i j k s t r a
若 s s t t 2 2
view code #include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
using namespace std;
const int maxn = 5e3 + 5 ;
const int maxm = 1e5 + 5 ;
const int inf = 0x3f3f3f3f ;
struct node {
int to, nxt, w, c;
} edge[maxm];
int n, m, s, t;
int cnt = 1 , mf, mc;
int head[maxn], pre[maxn];
int dis[maxn], h[maxn], flow[maxn];
void add_edge (int u, int v, int w, int c) bool dijkstra () int , int >, vector<pair<int , int > >, greater<pair<int , int > > > pq;
memset (pre, 0 , (n + 1 ) * sizeof (int ));
memset (flow, 0 , (n + 1 ) * sizeof (int ));
memset (dis, 0x3f , (n + 1 ) * sizeof (int ));
dis[s] = 0 ;
flow[s] = inf;
pq.push (make_pair (0 , s));
while (!pq.empty ()) {
int d = pq.top ().first;
int u = pq.top ().second;
pq.pop ();
if (d > dis[u]) {
continue ;
}
if (u == t) {
break ;
}
for (int i = head[u]; i; i = edge[i].nxt) {
int v = edge[i].to, w = edge[i].c + h[u] - h[v];
if (edge[i].w && (dis[v] > dis[u] + w)) {
dis[v] = dis[u] + w;
pre[v] = i;
flow[v] = min (flow[u], edge[i].w);
pq.push (make_pair (dis[v], v));
}
}
}
return (dis[t] < inf);
}
void primal_dual () while (dijkstra ()) {
mf += flow[t];
mc += (dis[t] - h[s] + h[t]) * flow[t];
for (int i = 1 ; i <= n; i++) {
h[i] = min (h[i] + dis[i], inf);
}
for (int i = t; i != s; i = edge[pre[i] ^ 1 ].to) {
edge[pre[i]].w -= flow[t];
edge[pre[i] ^ 1 ].w += flow[t];
}
}
}
int main () int u, v, w, c;
scanf ("%d%d%d%d" , &n, &m, &s, &t);
for (int i = 1 ; i <= m; i++) {
scanf ("%d%d%d%d" , &u, &v, &w, &c);
add_edge (u, v, w, c);
add_edge (v, u, 0 , -c);
}
primal_dual ();
printf ("%d %d\n" , mf, mc);
return 0 ;
}




【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理
· 单元测试从入门到精通
· 上周热点回顾(3.3-3.9)
· winform 绘制太阳,地球,月球 运作规律